Cross Ventilation for Swamp Cooler Cooling, ANSYS Fluent CFD Simulation Training
$80.00 Student Discount
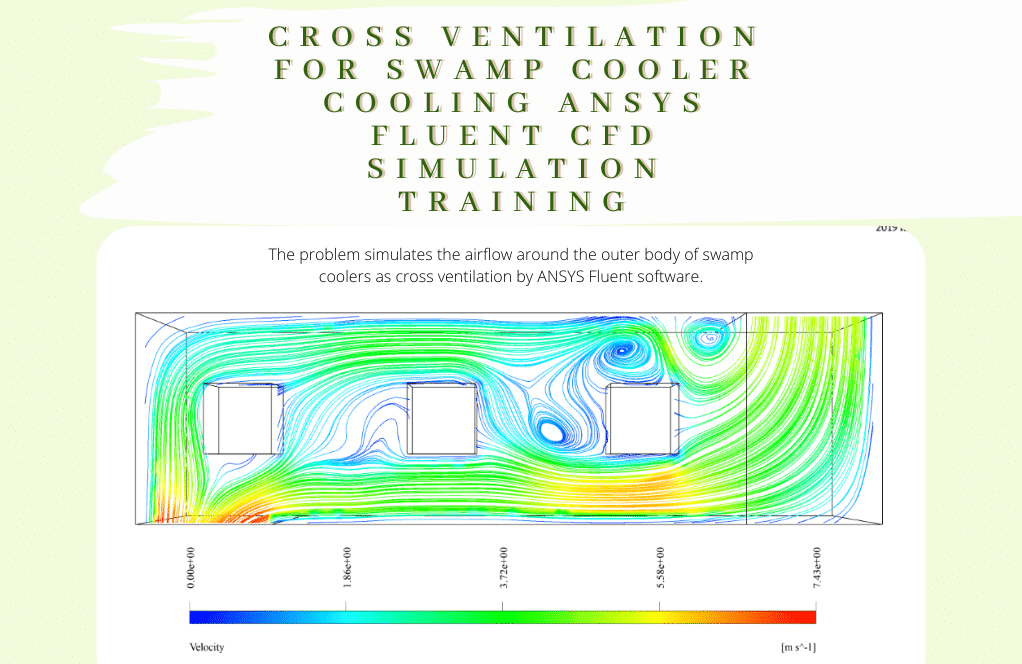
- The problem simulates the airflow around the outer body of swamp coolers as cross ventilation by ANSYS Fluent software.
- We have designed the geometry using ANSYS Design modeler software.
- We created the mesh on this geometry using ANSYS meshing software. The element number is 84594.
- The Energy equation is ON to capture the temperature.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Cross Ventilation Project Description
The problem simulates the airflow around the outer body of swamp coolers as cross ventilation via ANSYS Fluent software. We perform this CFD project and investigate it by CFD analysis.
We design the present 3-D model using Design Modeler software. The model meshing has been done using ANSYS Meshing software. The mesh type is unstructured, and the element number is 84594.
The performance of water cooler systems is such that the outside, warm air is sucked into their building and meets the pumped water flows in the cooler.
The water flow receives the latent heat it needs to evaporate from the perceptible heat of the incoming airflow, and as a result, it evaporates. In this way, the air loses its temperature as it loses its heat, and on the other hand, it gets wet by mixing with the water vapor from evaporation.
Therefore, cool, humid air enters the room through the air conditioner vents. There are several ways to increase the efficiency of this type of air conditioner and reduce its consumption.
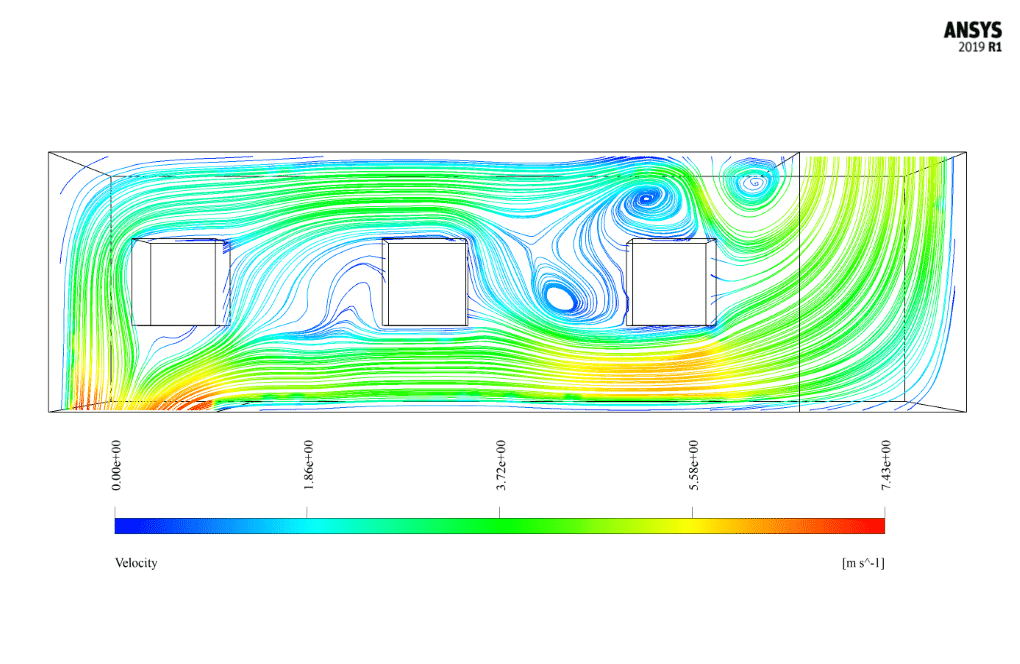
One way to increase efficiency is to create turbulent air around the outside walls of the air conditioner, which we can make possible by creating a special air circulation space like a windcatcher.
Due to its structure, this windcatcher can completely circulate the air inside and around the outer body of the air conditioner. As a result, cooling these warm exterior walls strengthens and accelerates the water flow’s evaporation process and reduces air temperature.
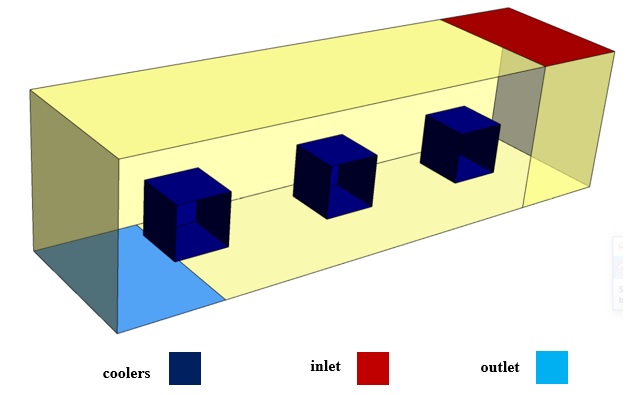
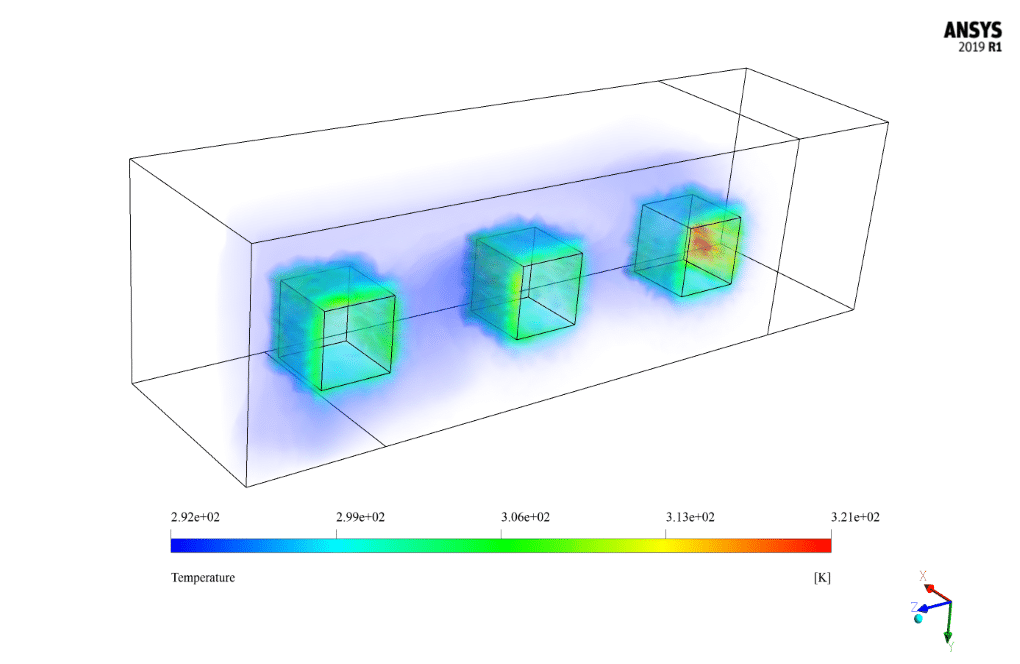
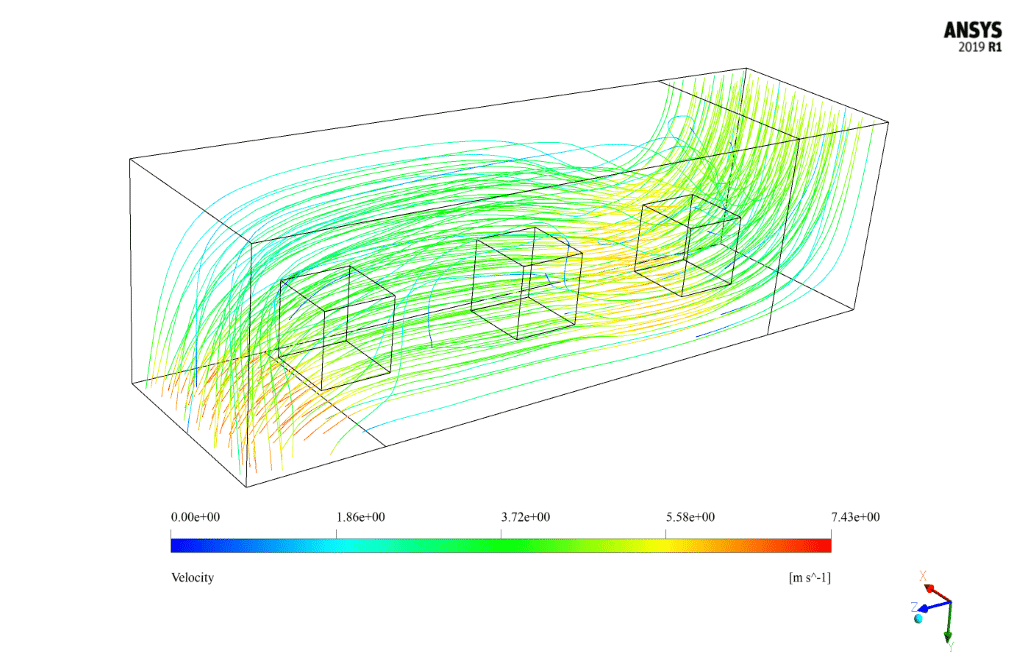
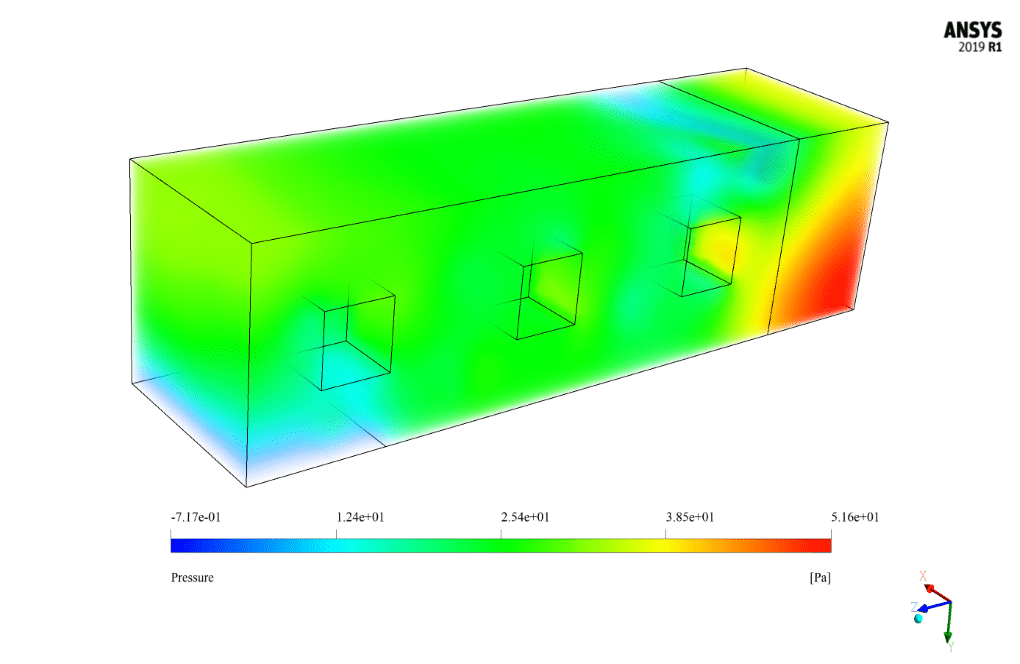
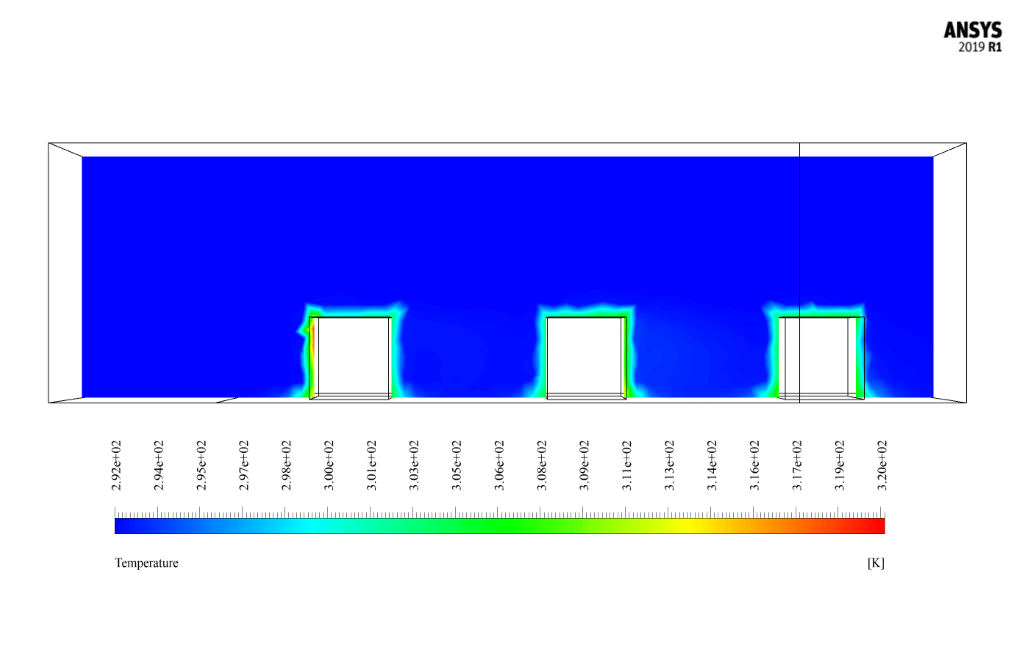
The present CFD simulation assumes that all external faces of these three coolers have a constant thermal flux equal to 200 W.m-2. Airflow enters the space around the three coolers at a velocity of 5 m/s and a temperature of 292 K from the windshield inlet of the air conditioners. The cooling process takes place by cooling the air circulation in this area.
Methodology
We use the Standard Wall Function and K-epsilon Standard model for the turbulence equation. Also, the Energy equation is On to capture the temperature.
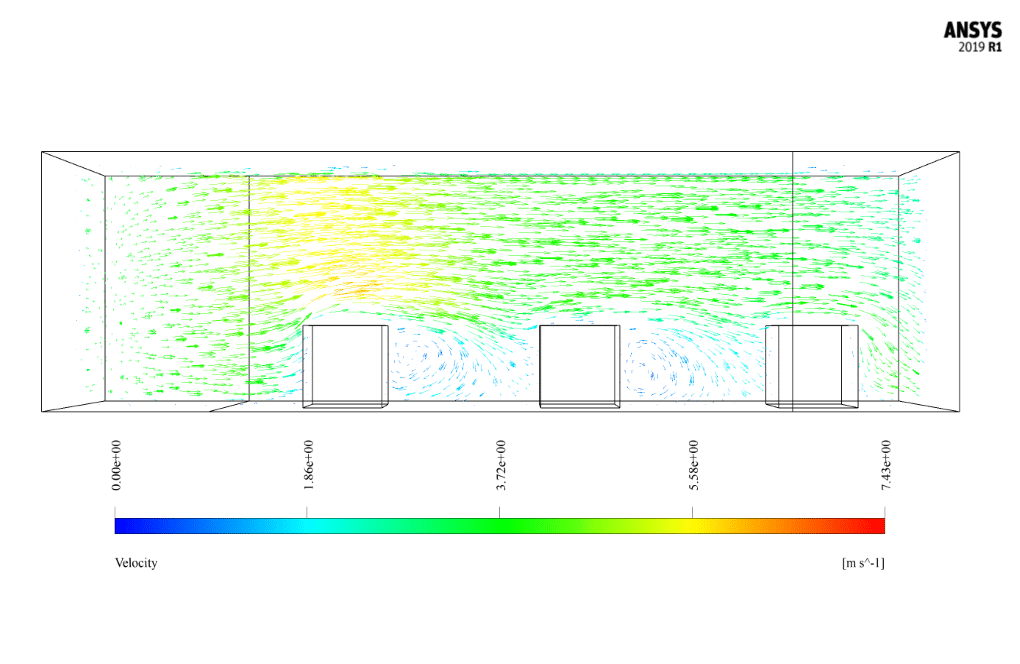
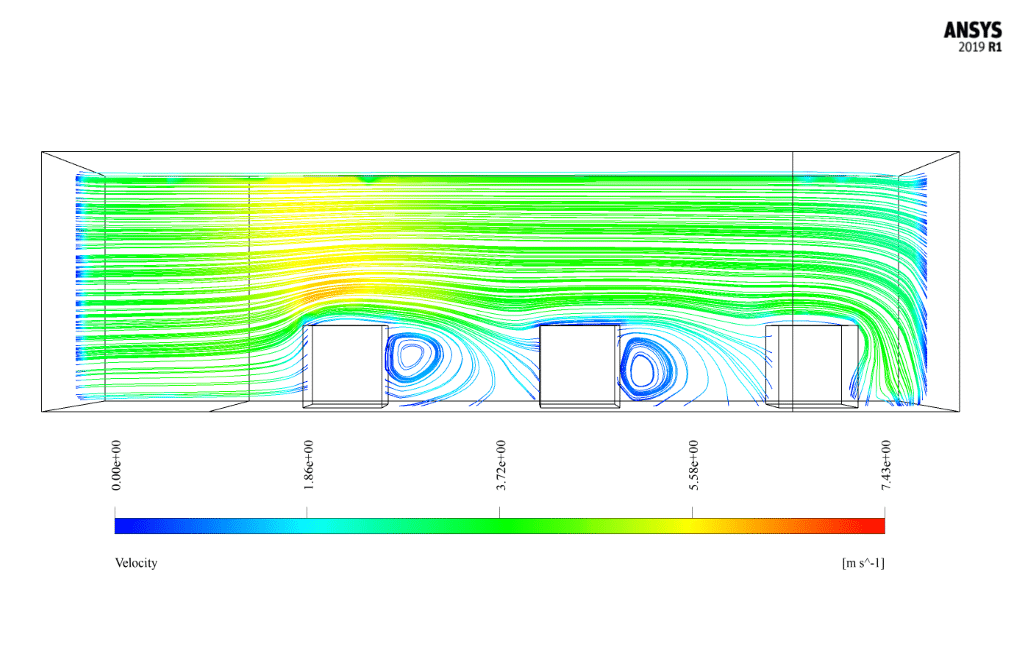
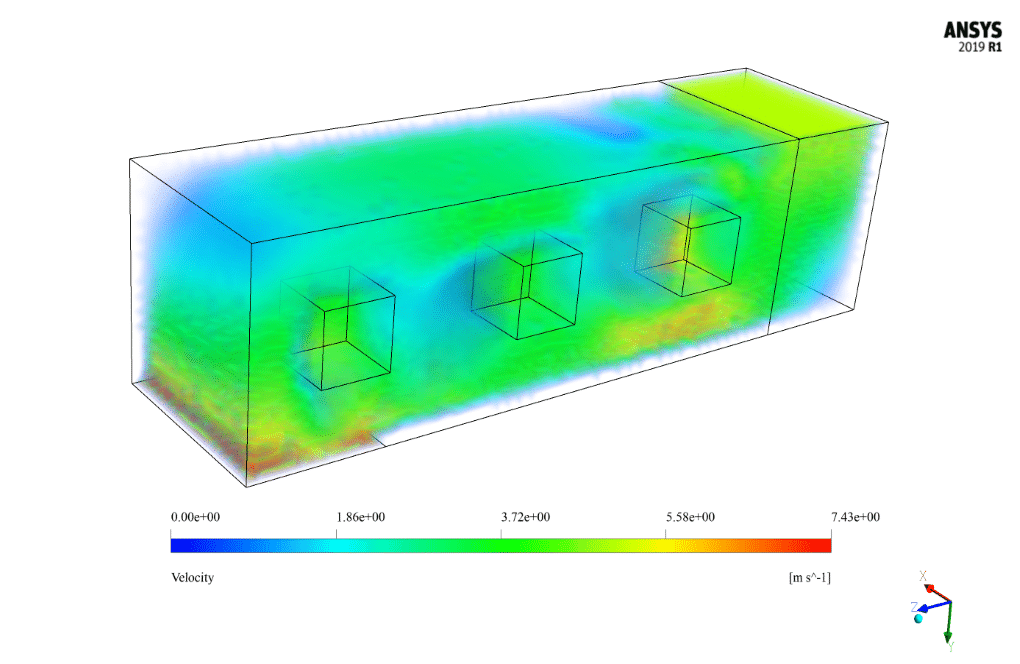
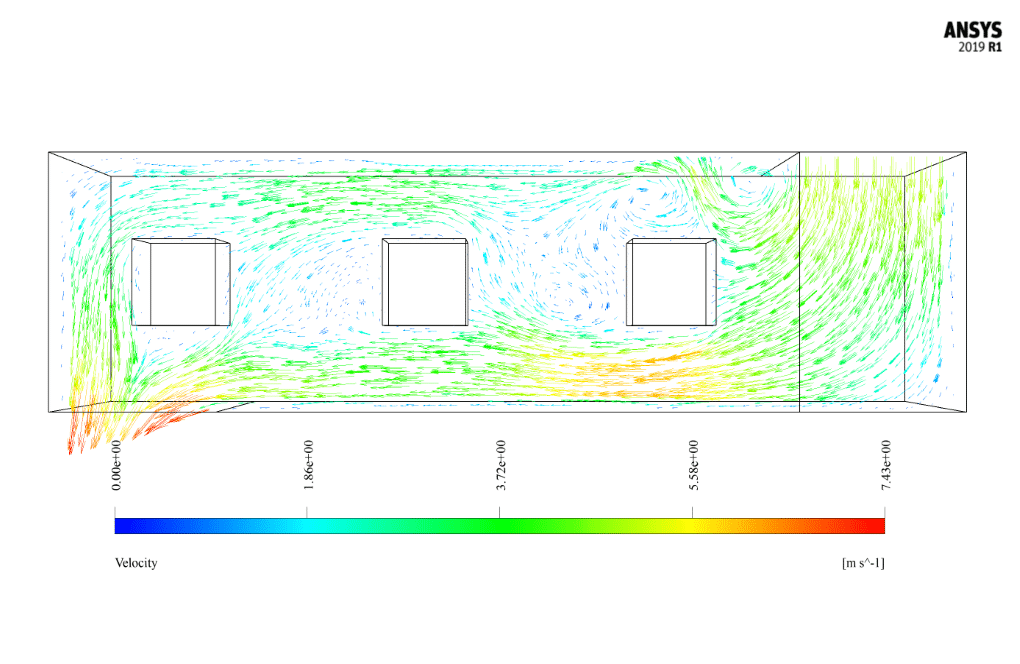
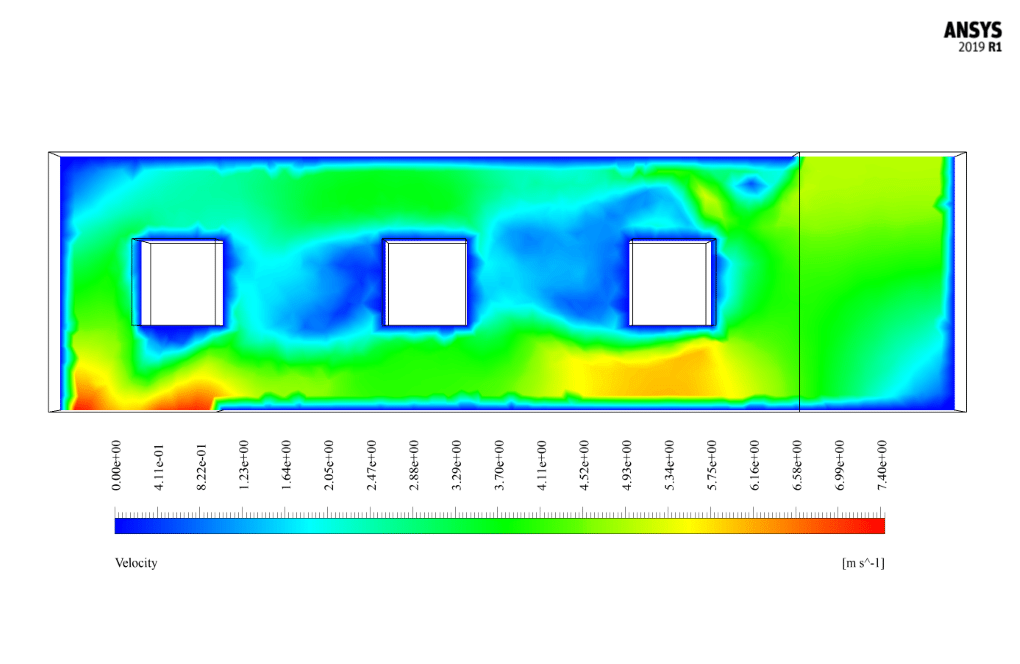
Cross Ventilation Results
After the solution, we obtain 2D and 3D contours related to pressure, temperature, and velocity. We also obtain 2D and 3D velocity vectors. We draw 2D contours and vectors in two sections, YZ and XZ.




Miss Eleonore Lehner MD –
I prepared this product, and I am completely satisfied.
Chloe Baumbach –
How do you ensure the accuracy of your simulations?
MR CFD Support –
Our simulations are based on well-established physical and mathematical principles. We also validate our simulations against experimental and theoretical results to ensure their accuracy.
Wilma Ebert Sr. –
Your Cross Ventilation for Swamp Cooler Cooling simulation is very detailed. Great work!
Miss Ophelia Feil –
I am thrilled with how the simulation illustrated the effect of windcatchers to improve efficiency. But I am curious, were any specific challenges encountered while attempting to simulate the turbulence around the swamp coolers?
MR CFD Support –
Thank you for your kind words! In simulations like these, accurately capturing the complex turbulence around structures can pose a challenge due to the computational demand and the need for precise numerical schemes and meshing strategies. However, the use of robust turbulence models like the K-epsilon Standard and careful mesh resolution around the critical areas usually helps in overcoming these issues efficiently. If you have more technical questions or need another discussion, feel free to reach out!
Dr. Frederic Vandervort –
The training was instrumental in understanding the cross ventilation effect in swamp coolers. It helped me to visualize the process and grasp how coolers can be made more efficient.
MR CFD Support –
Thank you for your positive feedback! We are delighted to hear that our CFD simulation on cross ventilation in swamp coolers has provided you with a comprehensive understanding of cooler efficiency improvements. If you need further assistance or more in-depth knowledge on this domain, we are always here to help.
Prof. Jennie Conn –
The CFD project simulation for the swamp cooler’s cross ventilation sounds thoroughly conducted. The use of windcatchers seems innovative and might significantly enhance efficiency. This CFD simulation serves as a brilliant guide for understanding airflow around air conditioning units.
MR CFD Support –
Thank you for your positive feedback. We’re glad the detailed approach demonstrating the efficiency of cross ventilation in combination with the swamp coolers through our CFD simulation was insightful for you. We’re committed to providing comprehensive studies to aid in understanding these systems better. Should you have any further queries or need more detailed analysis, feel free to reach out!
Leopoldo Sporer III –
This swamp cooler CFD project presentation was comprehensive and tailored my understanding of cross ventilation’s effectiveness. Meticulous detail in the simulation procedure highlighted the real-world application of the concepts learned.
MR CFD Support –
Thank you for your kind words. We’re thrilled to hear our training on cross ventilation for swamp coolers in ANSYS Fluent was detailed and effective in enhancing your understanding. Your feedback is greatly appreciated!
Jovanny Bashirian I –
This detailed product sounds innovative! Thanks to the properly applied methodology, it seems perfect for grasping the complex interaction between airflow and cooler efficiency.
MR CFD Support –
Thank you for your positive feedback! We’re glad to hear that the methodology and detailed explanation provided in our training material have met your expectations. If you have any further questions or need additional insight into such simulations, feel free to reach out. We appreciate your engagement with our products!
Dr. Glenda Hane DDS –
This product helped me understand air circulation around coolers. Just send my thanks to the technical team for creating such a detailed CFD simulation!
MR CFD Support –
Thank you for your kind words. We are delighted to hear that our training contributed to your understanding of air circulation around coolers. Your appreciation means a lot to our technical team!