ScanEagle UAV(Drone) Acoustic Analysis: CFD Simulation by Ansys Fluent

Description

Acoustic Analysis: ScanEagle UAV(Drone) CFD Simulation Training

Introduction

In ScanEagle Drone project, we analyze a ScanEagle Drone acoustically and examine the sources of sound production. We also define receivers around the drone to observe and examine the amount of sound received by the receivers.

A small, long-endurance, low-altitude unmanned aerial vehicle (UAV) used for reconnaissance is the Boeing Insitu ScanEagle. It is a Boeing subsidiary.

ScanEagle Drone has a 1,500km range and can run continuously for more than 28 hours. The air vehicle’s operating range is 80 to 126 km/h, and its level flying cruise speed is 90 km/h. The vehicle can climb at a maximum velocity of 150 meters per minute, reaching an altitude of 4,880 meters.

A ScanEagle Drone is modeled in this simulation using ANSYS Fluent software. The device moves at a speed of 27.8 m/s while the propeller rotates at an angular velocity of 1200 rev/min.

The geometry of the present model is three-dimensional and has been designed using Design Modeler software. We do the meshing of the present model with ANSYS Meshing software. The mesh type is Polyhedra, and the element number is 3,213,450.

Methodology

The topic of acoustics is a very widely used and interesting topic in computational fluid dynamics. In this topic, we deal with waves and consequently with pressure.

For this project, we have used two models, BroadBand Noise and Ffowcs Williams and Hawkings (FW_H), and we have explained the settings for both models and examined the differences between the two models. First, we simulated the BroadBand Noise model steady, and after convergence and aerodynamic stability of the problem, we change the solution model to FW_H and perform the solution transient. If we activate the FW_H model from the beginning, we will hardly reach convergence and the solution may even diverge.

In the BroadBand Noise model, we extracted the Acoustic pressure level contour in decibels for the blades and in the FW_H model, we defined 7 receivers around the UAV and extracted the following results:

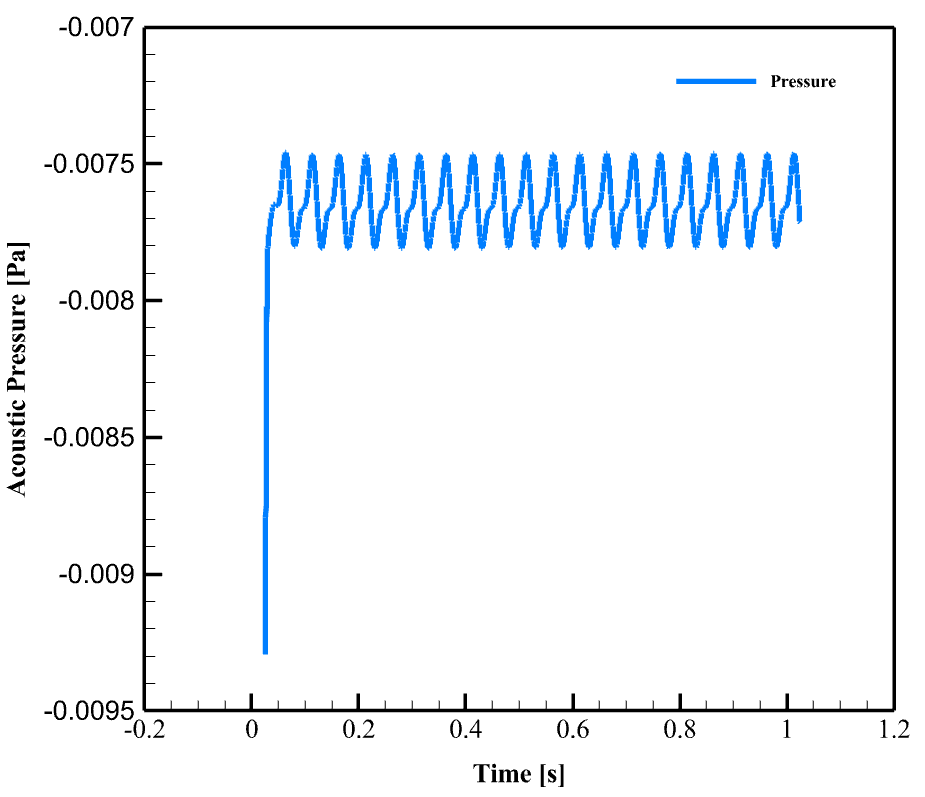
• Acoustic Pressure vs Time: This pressure is actually the acoustic signal calculated from the Ffowcs–Williams–Hawkes (FW–H) equation, which is due to the fluctuations in the flow around the propellers.
• Sound Pressure Level: SPL is the “physical intensity of the produced sound” and is directly proportional to the sound energy, without the interference of the human ear.
• A-Weighted Sound Pressure Level: A-weighting is a filter-like function that simulates the sensitivity of the human ear. Instead of the physical SPL, the sound level in this graph is calculated to represent the “actual loudness perceived by the ear.”
• B-Weighted Sound Pressure Level: The B-weighted filter is weaker than the A-weighted filter and only attenuates a portion of the low frequencies.
• dpdt RMS: The values ​​in this contour indicate the intensity of the time-dependent pressure fluctuations at each point on the surface.

Results

In the BroadBand Noise model, we can observe the Acoustic pressure level contour in decibels. Acoustic Power Level actually represents the sound power produced by the entire or part of the surface of an object and is expressed in decibels (dB). Comparing this contour with the Turbulent intensity contour, we find the similarity between them. In reality, the Acoustic pressure level is calculated and displayed based on the Turbulent Intensity. Therefore, wherever the Turbulent intensity is high, the acoustic pressure is also high.

Sometimes, slight differences appear between these two parameters, near the object (source area), the similarity is high and at greater distances, the patterns may different because the intensity depends on the direction of propagation and wave attenuation.

In the FW_H model, the extracted data for one of the defined receivers can also be viewed.

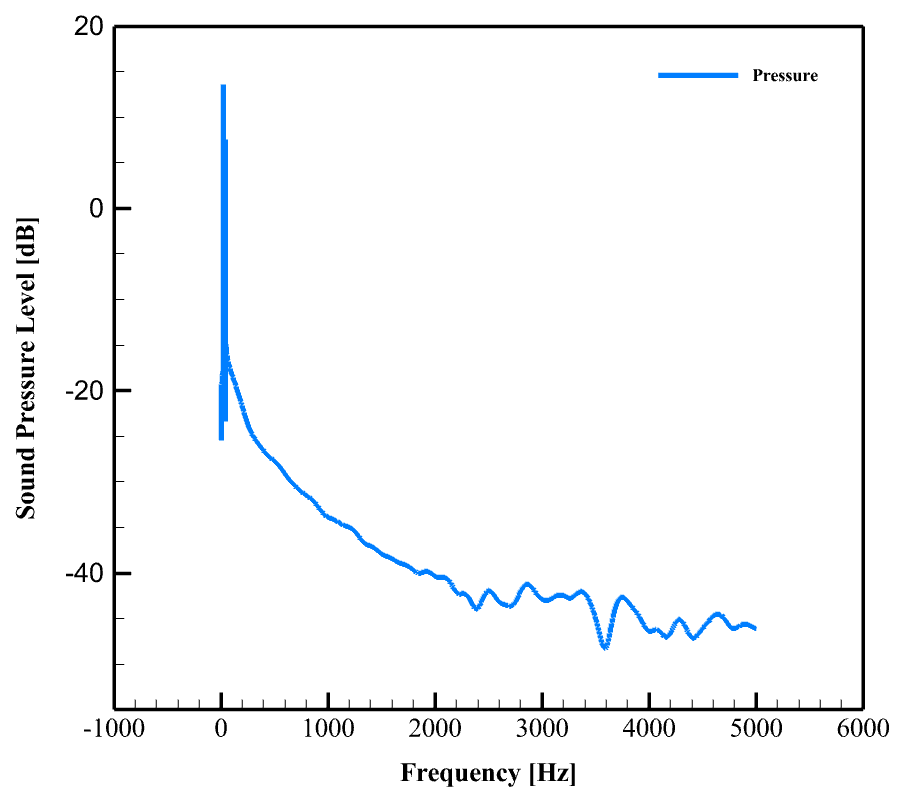
SPL (Sound Pressure Level)  graph is obtained by applying a Fourier transform (FFT) to the time domain signal and shows the noise characteristics in the frequency domain. A very sharp and loud peak is observed at a very low frequency (near 0 Hz, probably a specific discrete frequency) that reaches about 15 dB. After this peak, the sound pressure level decreases rapidly and then gradually with increasing frequency. There is a general decreasing trend in SPL with increasing frequency, but small fluctuations (around 3500-4000 Hz) are also seen in the high frequency parts.

This plot shows the frequency spectrum of the unweighted noise. The very strong and sharp peak at low frequency clearly indicates a tonal component or a narrowband noise source. This component is probably the same vorticity frequency that was seen as periodic oscillations in the time plot.

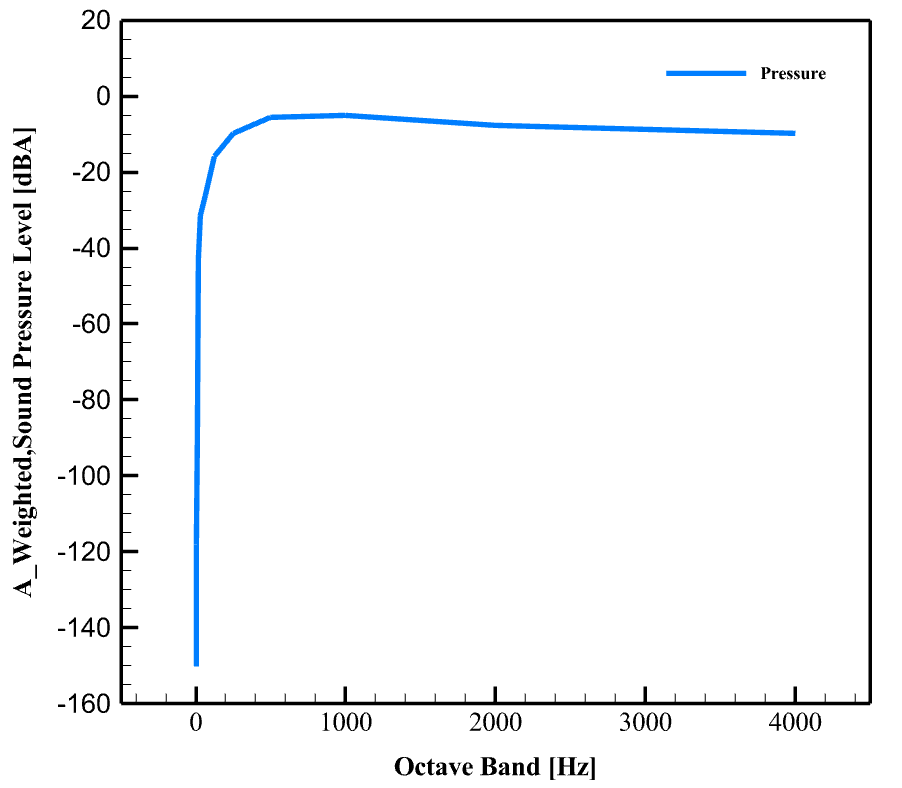
The graphs below show the sound pressure level in wider frequency bands (octave) and use A and B weighting filters. 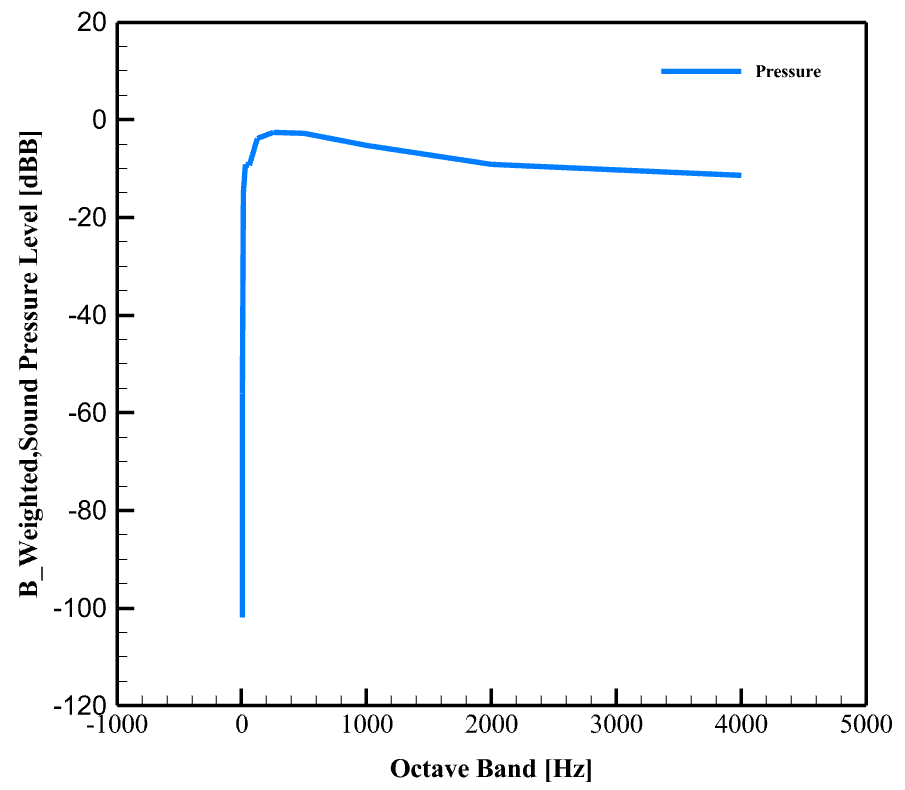Octave bands collect noise energy in specific frequency ranges rather than representing individual frequencies.

A-weighting simulates the human auditory response, meaning it reduces low and very high frequencies to make the graph more consistent with what the human ear hears. B-weighting also simulates the human auditory response, but it provides less reduction at low frequencies than A-weighting and was used more for older measurements. A very sharp increase in the sound pressure level is observed at low frequencies (near 0 Hz). The peak sound pressure level is about 0 dB. After the peak, the sound pressure level decreases rapidly and then stabilizes at higher frequencies (above about 1000 Hz) at a value of approximately -10 to -15 dB.

Finally, the SPL is the actual sound intensity from the drone, derived from the pressure field calculated by FW–H, the A-weighted SPL (dBA) is the sound level that humans actually hear (the hearing threshold is taken into account), and the B-weighted SPL (dBB) is an approximation of the perceived sound at medium intensities. Comparing these three shows the difference between the physical energy of the sound and the perceived energy; in drones, the lower frequency (BPF) is usually clear in SPL but less so in dBA.

The Acoustic Pressure graphs show the time variations of the sound pressure ( p’(t) ) at the receiver location. This pressure is actually the acoustic signal calculated from the Ffowcs–Williams–Hawkes (FW–H) equation, which is due to the fluctuations in the flow around the propellers. At a time of about 0.1 second, a sudden change in pressure is observed, from a very negative value to about -0.0075 Pascal. This is an initial transient behavior. After this transient behavior, the sound pressure begins to oscillate regularly and with almost constant amplitude, around a mean value of about -0.0076 Pascal. These oscillations are quite periodic, with a large number of cycles seen in the displayed time interval.

This graph shows the time history of the sound pressure at a given point (receiver). Periodic oscillations indicate the presence of one or more dominant frequencies in the generated noise. This behavior is usually observed in cases where the flow around an object causes periodic phenomena such as vortex shedding. The negative value of the average pressure may be due to the flow characteristics or simulation settings, but more importantly, the sound pressure fluctuates around this value.

The last data that we will discuss in this report is the dpdt RMS contour. The values ​​in this contour indicate the intensity of the time-dependent pressure fluctuations at each point on the surface.

High dp/dt values ​​indicate rapid and severe pressure changes at those points. These rapid pressure changes are the main source of acoustic noise generation. The concentration of high dp/dt values ​​at the blade tips and edges is quite logical and expected for a rotating propeller.

This contour clearly shows the physical sources of noise that lead to the tonal and broadband peaks observed in the frequency domain plots. That is, these pressure fluctuations at the propeller surface propagate sound waves into the environment that we see in the SPL plots.

This description is a brief overview of one of the receivers defined in this project. In the training video of ScanEagle Drone, we analyze and explain the extracted data and compare them with each other in more detail.