Population Balance Model (PBM)

What is the Population Balance Model (PBM)?

The Population Balance Model (PBM) is one of the concepts in collective phenomenology. This concept is used when components or particles move through state space or during birth and death processes, the current particles are destroyed, and new particles are produced.

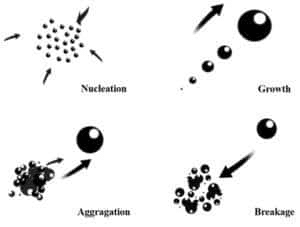
The main application of this model is related to currents that include a second phase with a specific size distribution. Particle size distribution, including solid particles, bubbles, droplets, etc., can evolve due to transfer within the base fluid or due to the occurrence of chemical reactions in a multiphase system. Evolutionary processes include nucleation, growth, Aggregation, and Breakage.

Consider, for example, a precipitation process. This process is related to forming solid particles from a liquid solution and consists of several processes, including nucleation, growth, Aggregation, failure, etc. These processes increase or decrease the number of particles of a specific size. So it can be said that PBM means balance in the number of particles with a particular state (for example, particle size in the example).

The mathematical technique known as the Population Balance Model (PBM) is employed to characterize the distribution of attributes in a population of particles or droplets. It has widespread application in chemical engineering and biology.

The underlying assumption underpinning PBM is that there is room for large variation in system behavior due to differences in particle properties. By taking into account the distribution of these features, the PBM enables us to foretell the system’s behavior.

Population balance equations (PBEs) are a common integro-differential representation of the PBM. Growth, nucleation, aggregation, and breakdown are only some of the processes that the PBE details in describing how the population (the number of particles with a specific quality) evolves.

An easy-to-understand PBE is as follows:

∂n(ξ,t)/∂t + ∂(G(ξ,t)n(ξ,t))/∂ξ = B(ξ,t) – D(ξ,t)n(ξ,t)

where:

– n(ξ,t) is the number density function, which gives the number of particles with property ξ at time t,

– G(ξ,t) is the growth rate function,

– B(ξ,t) is the birth rate function, and

– D(ξ,t) is the death rate function.

PBM Application

The particle PBM is used in various topics, including crystallization processes, precipitative reactions, bubble columns, sprays, polymerization with fluidized bed, grain Granulation, liquid-liquid emulsion, aerosol flows, leaching metallurgy, liquid-liquid extraction, gas-liquid dispersion, liquid-liquid reactions, biology, etc.

Within a chemical or biological system, the Population Balance Model (PBM) provides a mathematical description of the distribution and variation of attributes within a population. Chemical engineering, pharmaceuticals, mining, and materials science are just a few of the many fields that make use of PBM.

PBM’s Various Uses

• Particle size distribution in chemical engineering includes crystallization, fluidization, and aerosol processes, all of which can be modeled using PBM.
• Crystallization processes, which affect the size, shape, and structure of drug particles and thus the medicine’s efficacy and safety, are modeled and controlled using PBM in the pharmaceutical industry.
• Particle size distribution prediction in grinding circuits is an important use of PBM in mining and materials science.
• In the biotechnology industry, PBM is used to simulate the proliferation of cells in bioreactors, a crucial step in the creation of biopharmaceuticals and other bioproducts.
• Aerosol production and growth may be modeled with PBM in environmental engineering, providing insight into the causes of air pollution and global warming.

An elementary PBM equation looks like this:

dN/dt = G(N) – A(N)N

Where N is the number of particles, G(N) is the particle growth rate, and A(N) is the particle aggregation rate. This equation describes how the number of particles changes over time due to growth and aggregation.

PBM Equation Application

A PBM equation is needed to describe population or particle density changes in multiphase flows involving a given size distribution. This balance equation is commonly known as the PBM equation. In fact, in multiphase currents with particle distribution and the equilibrium equations of momentum, mass, and energy, the population balance equation must also be solved.

Population Balance Equations are defined in several branches of modern science (mainly chemical engineering). These equations describe the gradual evolution of particles and the motion of a particle population. In other words, these equations define how individual particle populations develop over time in a series of distinct thermophysical properties. These equations include a set of integral-partial differential equations (PDE), each of which presents the field behavior of a population of particles based on the behavior of each independent particle in the local state.

The PBM is a mathematical framework for studying how the characteristics of a population change over time. It can be used in chemical engineering, biotechnology, ecology, and other disciplines. Distributional changes over time can be described by a partial differential equation known as the PBM equation. In chemical engineering, for example, the PBM equation can be used to model the number of cells in a bioreactor or the size distribution of particles in a suspension or emulsion.

An elementary PBM equation looks like this:

∂f/∂t + ∂(Gf)/∂x = S(x,t)

In this equation:

– f is the distribution function.

– t is the time.

– x is the property of interest (such as particle size).

– G is the growth rate function.

– S is the source term, which represents any external influences.

The solution to this equation gives the distribution function f as a function of x and t, which provides information on how the distribution of the property x changes over time.

How can PBM CFD simulation be applied in Engineering?

Numerous engineering disciplines, especially those concerned with particle systems, can benefit from CFD’s Population Balance Model (PBM). The following are examples of such things:

Chemical Engineering

Particle size distribution is a key aspect in many chemical processes, hence PBM-CFD is used in chemical engineering to simulate and optimize processes including crystallization, polymerization, and precipitation.

Crystallization

The crystallization process can be modeled using PBM-CFD, including nucleation, growth, and aggregation. Because crystal size has a direct effect on product quality, this is especially important in the pharmaceutical and food processing industries.

Polymerization

PBM-CFD is useful for predicting the molecular weight distribution of finished polymers and understanding the kinetics of polymer development during manufacture.

Precipitation

PBM-CFD is used to model precipitation processes, which have relevance in fields including wastewater treatment, mining, and materials research.

Mechanical Engineering

In mechanical engineering, PBM-CFD can be used to model the response of particle systems to fluid flows in devices like cyclone separators and fluidized bed reactors.

Fluidized Bed Reactors

Combustion, gasification, and drying are just some of the many applications for them. PBM-CFD’s ability to forecast particle size distribution, velocity, and temperature profiles can be used to improve the efficiency of various processes.

Cyclone Separators

Cyclone separators, to be precise. Cyclones can be modeled using PBM-CFD to predict their separation efficiency when applied to air, gas, or liquid streams.

Environmental Engineering

Aerosols and other particle pollution in the atmosphere can be modeled using PBM-CFD in environmental engineering.

Air Quality Modeling

Air quality management and environmental impact assessments rely heavily on PBM-CFD’s ability to anticipate the dispersion and deposition of particle contaminants.

Biomedical Engineering

Biomedical engineering can make use of PBM-CFD to model how drugs disperse through the body.

Drug Delivery Systems

Modeling the release and spread of drug particles from delivery methods including inhalers and injectable medication formulations is possible with PBM-CFD. This has the potential to enhance the efficiency of drug administration.

MR CFD services in the PBM Simulation for Engineering and Industries

With several years of experience simulating various problems in various CFD fields using ANSYS Fluent software, the MR CFD team is ready to offer extensive modeling, meshing, and simulation services. Simulation Services for PBM CFD simulations are categorized as follows:

• CFD Simulation of distribution kinetics of plastics decomposition
• Crystallization processes CFD Simulation
• CFD Simulation of the liquid-liquid extraction column
• CFD Simulation of foam transport in porous media
• Multiphase CFD simulation (nucleation, coalesce …)
• CFD Simulation of gas-liquid dispersion and liquid-liquid reaction

Computational fluid dynamics (CFD) is used by MR CFD, a specialized service, to simulate and analyze fluid flow and heat transfer issues. They have a staff of professionals who can help with a wide range of engineering and industrial projects.

Several areas of PBM can benefit from MR CFD:

• Model Development and Simulation

They can aid in the creation of particle-based model (PBM) simulations for processes like crystallization and polymerization, among others. The movement of particles through a fluid medium can be simulated by using these models.

• Analysis and Optimization

Once the models have been constructed, MR CFD can examine the findings to get insight into the system’s behavior, at which point optimization can begin. They may also offer advice on how to enhance the system’s functionality.

• Software Training and Support

MR CFD also offers training and assistance for a wide range of CFD software. If you’re trying to develop skills in-house, this can be quite helpful.

PBM in ANSYS Fluent

To perform a Population Balance Model (PBM) in ANSYS Fluent, here are the steps you need to follow:

– Setup the Simulation: Start by setting up your simulation in Fluent as you normally would. This includes setting up the geometry, mesh, materials, boundary conditions, etc.

File > Import > Mesh…

Define > Models > Solver…

– Enable the Population Balance Model: Go to the ‘Models’ menu, and select ‘Multiphase’. Here, you will find the ‘Population Balance Model’ option. Enable it.

Define > Models > Multiphase…

– Define the Population Variables: You’ll need to define the population variables. This includes the number of classes, the size range, and the initial number density.

Define > Models > Population Balance > Classes…

– Set Up the Population Balance Equations: Set up the equations that will govern the population balance. This includes the birth and death terms, as well as the aggregation and breakage terms.

Define > Models > Population Balance > Birth and Death…

– Run the Simulation: Once everything is set up, you can run the simulation. Monitor the results and make sure the solution is converging.

Solve > Initialize > Initialize…

Solve > Run Calculation…

– Analyze the Results: After the simulation is complete, you can analyze the results. This includes looking at the number density distribution, the average size, and other population parameters.

Results > Graphics and Animations…

PBM MR CFD Projects

Nucleation

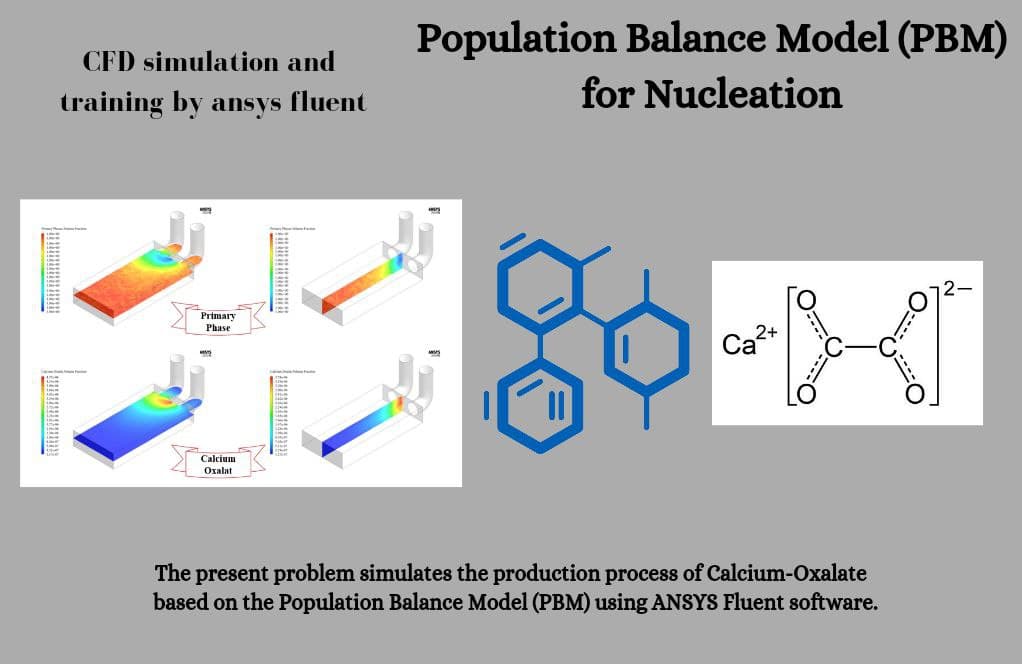
First, the calcium-oxalate synthesis process is modeled, and then the PBM is studied concerning particle generation, growth, and dislocation. From one tube, just a stream of water with calcium is injected, and from the other tube, only a stream of water with oxalate is injected; this is how the mechanism of the examined system works.

After the two streams meet, a chemical reaction takes place in which calcium and oxalate combine to form calcium-oxalate. This software simulation procedure requires the use of multiphase and species transport models.

It’s also important to turn on particle-based modeling, chemical reactions, and mass transfer. The primary phase is a solution of water, calcium, and oxalate, as defined by the Eulerian multiphase model. Calcium oxalate forms as a byproduct of the first phase.

A chemical reaction is thus defined as part of a multiphase flow. In the first stage, calcium and oxalate react as reactants, leading to the formation of calcium-oxalate. Arrhenius is used to describe the rate of this reaction, and the activation energy is calculated to be 1e + 8 j.kg-1.mol-1. The process of mass transfer between materials must be defined in addition to the chemical reaction itself.

To characterize the process by which water, calcium, and oxalate are transformed into calcium-oxalate, it is necessary to specify three distinct phases of mass transfer. In addition, the initial phase of the species transport model must be defined as a slurry of water, calcium, and oxalate.

It is feasible to investigate the behavior pattern of particles created in the secondary phase after defining the process of conversion of primary phase materials to the secondary phase and the occurrence of the chemical reaction. The created particle’s behavior can be studied with the population balance model (PBM), which can then be used to forecast the density or population of particles in a certain size range.

There are many steps involved in the formation of multiple particles in an environment, from the initial nucleation to the growth of produced particles to the aggregation of several small particles and the breakdown of a large particle into smaller ones.

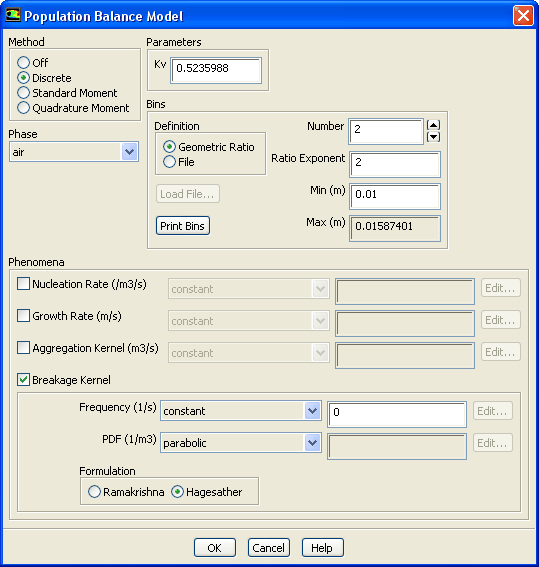
This simulation makes use of the discrete approach, one of several available in the software for defining the PBM. To estimate the population or density of particles in each size range, it is necessary to create multiple bins for a variety of particle sizes.

It’s worth noting that inductive reasoning and a multi-step simulation solution based on trial and error are behind figuring out the total number of categories and the scope of their definitions. For this simulation, we employ 48 bins, narrowing the allowable range of particle sizes from roughly 5e-7 m in diameter to about 2.9345 e-5 m in diameter.

In addition, the simulation assumes that only nucleation and growth processes take place and that aggregation and breakage do not. The initiation and development rates are specified by a UDF function. Furthermore, the fluid flow equations are solved using the laminar model.

After running the simulation, a two-dimensional representation of the time-dependent mass fraction of the presently existent chemical species in each bin is obtained. This video is the 4th episode of the Population Balanced Model Training Course.

Crystallization

To create a crystal structure, solute particles undergo a fundamental process known as crystallization. Population balance models (PBMs) are useful tools for gaining insight into crystallization processes such as growth, nucleation, and size distribution. Supersaturation, temperature, blending, and contaminants are all taken into account. Crystallization behavior can be simulated and predicted by solving the population balance equation.

Crystal growth, nucleation, and size distribution can all be better understood by simulating the crystallization process with a population balance model. The fields of medicine, chemistry, food, materials science, and even energy storage can all benefit from this method. By learning how to manage the crystallization process, scientists can improve product quality, boost productivity, and progress in many other types of industries.

Several outlines are displayed, including the speed of the phases inside the domain, the distribution of bin classes, and the variation in the percentage of each bin. Heterogeneous reaction contour reveals that the line of greatest concentration of Ca and Carbonate ions coincides with the line of greatest reaction. What’s more, let’s pretend we can see the boundaries between various bin classes. When the volume percentage of each bin increases in the domain, suggesting the formation of a solid phase of calcium carbonate, the nucleation and growth phenomena are straightforward to comprehend. What’s more, let’s pretend we’re looking at a histogram of the data’s density. If the value of the number density is close to zero, then it is clear that more bins can be added and smaller bin sizes considered. In comparison, the smallest bin has a very high number density. One possible interpretation is that not all microscopic containers and dust particles are taken into account. Therefore, this issue can be fixed by using more conservative numbers for the minimum diameter in the PBM configuration. This video is the 2nd episode of the Population Balanced Model Training Course.

Aggregation and Breakage – Air Bubble

To better understand the dynamics and interactions of bubbles, a population balance model can be used to simulate their formation and collapse via a water column. Understanding the intricate processes of bubble breakup and coalescence is made possible by the population balance model, which takes into account the distribution of bubble sizes and tracks their evolution over time. Researchers can model bubble behavior and foretell how it will develop in a water column by solving the population balance equation.

A population balance model can be used to simulate the growth and decay of bubbles in a water column, providing a rich picture of bubble dynamics. There are uses for this method in the fields of chemical engineering, environmental research, food and beverage production, and oil and gas extraction. Researchers can enhance procedures, increase productivity, and develop numerous industrial fields simply by thinking about the bubble size distribution and how it changes over time.

Various trajectories are depicted, such as the speed of the phases inside the water column, the distribution of various bin classes, and variations in the percentage of each bin along the axis of the pipe. Due to interactions between the water and air phase, coalescence and breakdown occur, resulting in the production of other class bins; in the starting state of the model, the bin-3 fraction was set to 1 over the air inlet border. The resulting graphs reveal that the distribution of these classes is highly sensitive to both the time being monitored and the geographic region being examined. Finally, the histogram plot for the number density displays the distribution of each particle diameter according to its number density, providing insight into the relative abundance of different bin or bubble sizes. This video is the 3rd episode of the Population Balanced Model Training Course.

PBM Application in Industrial Companies

To represent the size distribution and composition of a collection of particles, such as droplets, bubbles, or crystals, a mathematical model known as a Population Balance Model (PBM) can be used. These models see extensive application in a variety of manufacturing settings, particularly the chemical, pharmaceutical, and food production sectors.

Implementing PBM in Manufacturing Organizations

Chemical Industry

PBMs are used to develop, optimize, and regulate processes using particle systems in the chemical sector. Examples of such procedures could be crystallization, granulation, and polymerization.

Pharmaceutical Industry

The pharmaceutical industry relies on PBMs in the process of medication development and manufacturing. They aid in the prediction of the particle size distribution in a pharmacological formulation, which has a significant impact on the efficacy of the drug.

Food Industry

Particle size distribution in food products is a key factor in the product’s texture and flavor; PBMs can help forecast this distribution.

Oil and Gas Industry

The oil and gas sector uses PBMs to foretell how oil or gas bubbles would behave in a reservoir or a pipeline.

Environmental Engineering

Engineering in the field of environmental science uses PBMs to simulate the actions of airborne particles to better understand how to eliminate them.

PBM’s Benefits for Business Use

Predictive Power

Particle-based models (PBMs) can anticipate the behavior of particulate systems under different situations, which can aid in the design and optimization of processes.

Flexibility

PBMs can be modified to describe a variety of particle systems, making them useful in many fields.

Insight into Process Dynamics

Understanding and better managing particulate systems is facilitated by PBMs because of the information they provide about the dynamics of these systems. Because of its predictive strength, adaptability, and capacity to reveal process dynamics, Population Balance Modeling (PBM) finds widespread use in a variety of industrial settings.

MR CFD Industrial Experience in the PBM Field

Some examples of PBM industrial projects recently simulated and analyzed by MR CFD in cooperation with related companies are visible on the MR CFD website.

You may find the Learning Products in the PBM CFD simulation category in the Training Shop. You can also benefit from the PBM Training Package, which is appropriate for Beginners, Intermediate, and Advanced users of ANSYS Fluent. Also, MR CFD is presenting the most comprehensive PBM Training Course for all ANSYS Fluent users from Beginner to Experts. Get more familiar with PBM concepts.

Our services are not limited to the mentioned subjects. The MR CFD is ready to undertake different and challenging projects in the PBM modeling field ordered by our customers. We even carry out CFD simulations for any abstract or concept Design you have to turn them into reality and even help you reach the best strategy for what you may have imagined. You can benefit from MR CFD expert Consultation for free and then Outsource your Industrial and Academic CFD project to be simulated and trained.

By outsourcing your Project to MR CFD as a CFD simulation consultant, you will not only receive the related Project’s resource files (Geometry, Mesh, Case, and Data, etc.), but you will also be provided with an extensive tutorial video demonstrating how you can create the geometry, mesh, and define the needed settings (preprocessing, processing, and postprocessing) in the ANSYS Fluent software. Additionally, post-technical support is available to clarify issues and ambiguities.