Finned Tube Radiator Heat Transfer CFD Simulation, ANSYS Fluent Training
$60.00 Student Discount
- The problem numerically simulates heat transfer inside a finned tube radiator using ANSYS Fluent software.
- We design the 3-D model by the Design Modeler software.
- We Mesh the model by ANSYS Meshing software, and the element number equals 2120802.
- The Energy Equation is activated to investigate heat transfer and temperature distribution.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Description
The problem simulates heat transfer inside a finned tube radiator using ANSYS Fluent software. We perform this CFD project and investigate it by CFD analysis.
The present model is designed in three dimensions using the Design Modeler software. The model includes a symmetrical radiator, which is semi-drawn due to its symmetrical geometric structure and avoids heavy calculations.
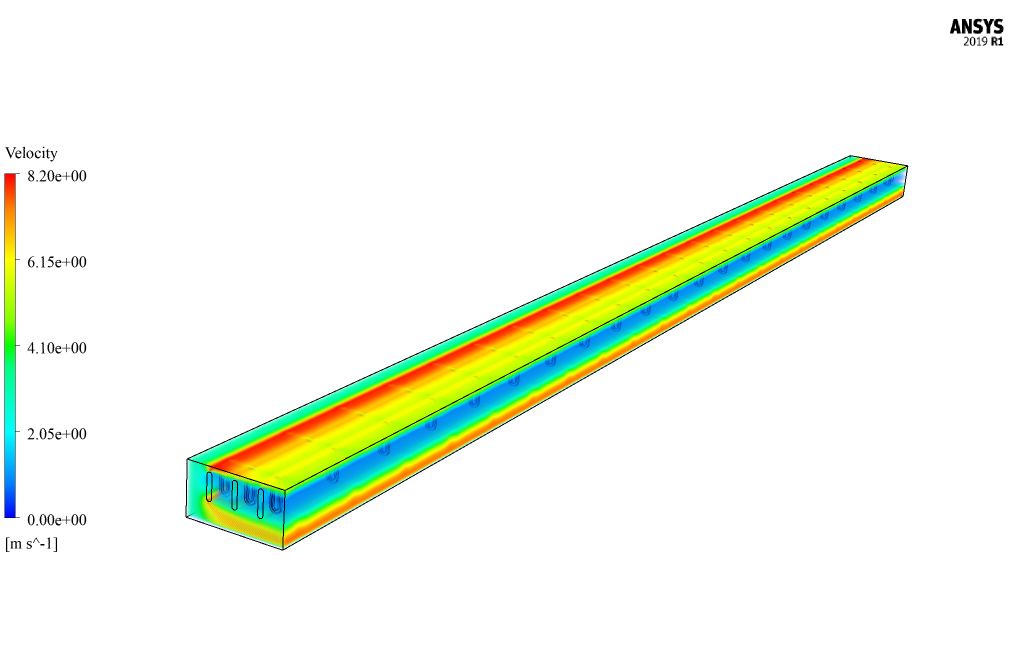
This radiator has an air inlet and outlet sections on both sides. Also, three pipes have been designed inside this radiator to pass water flow. On the body of each of the internal pipes, 22 rows of fins are used.
The meshing of the model was done using ANSYS Meshing software. The element number is equal to 2120802.
Radiator Methodology
The working mechanism of these radiators is such that the flow of hot water passes through the pipes inside the radiator; on the other hand, the airflow also passes through the pipes.
In this way, the airflow passes through the pipes carrying the hot flow, receiving their heat, and as a result, hot air flow is transferred to the outside environment.
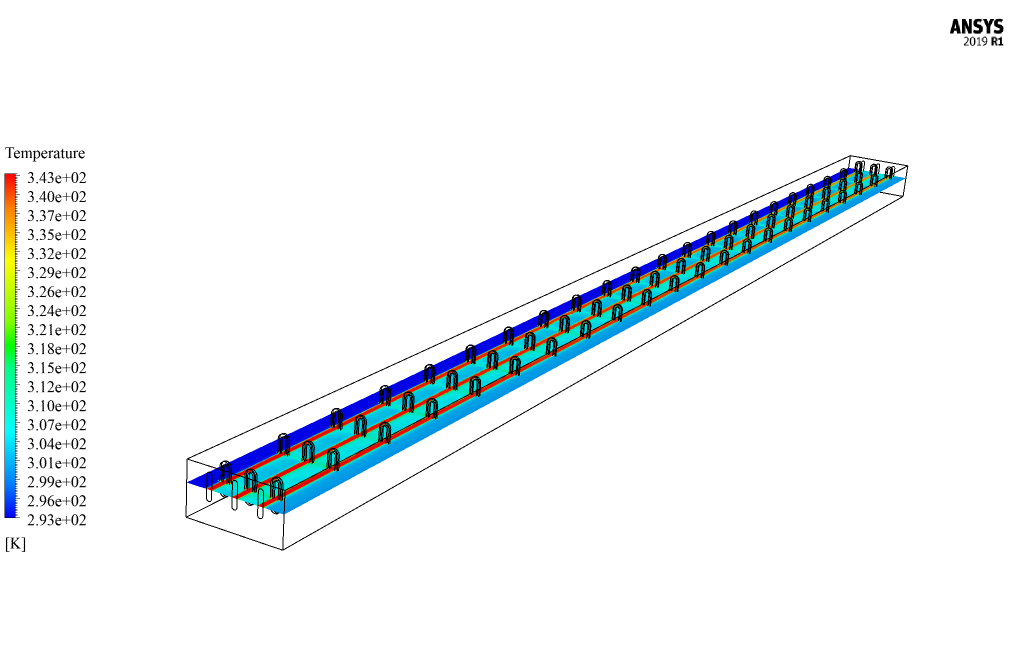
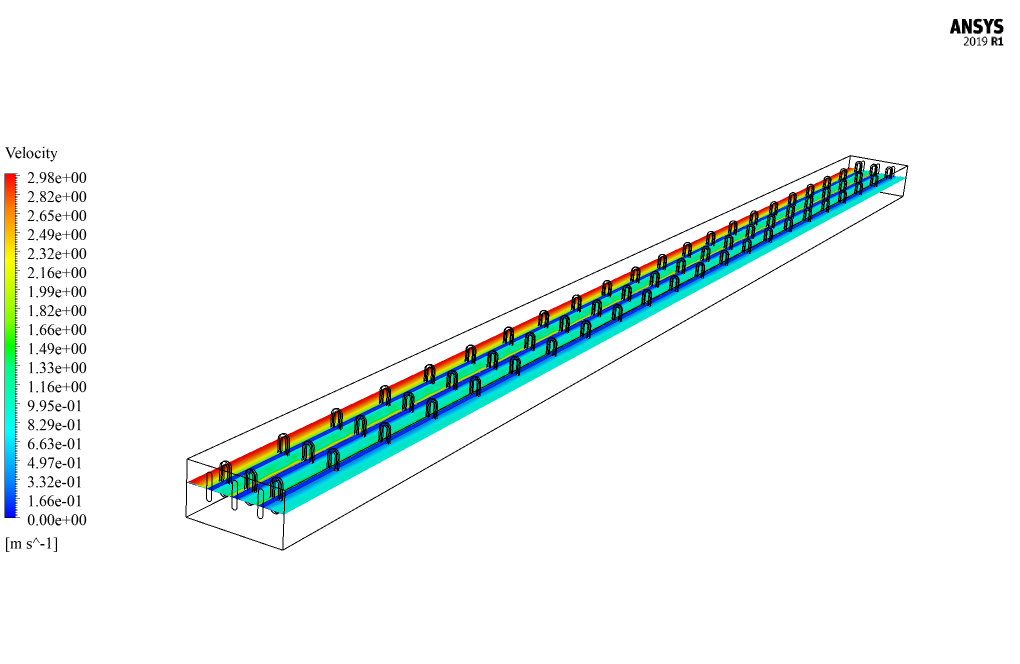
In this simulation, hot water flows at a speed of 0.1 m/s, and a temperature of 343.15 K flows through three pipes inside the radiator, and air flows at a speed of 3 ms-1 and a temperature of 293.15 K from It passes over this pipe.
To increase the amount of heat transfer inside the radiator, the amount of contact surface between cold air and hot water flow has been increased by using fins, and as a result, 22 rows of fins have been installed on each pipe carrying hot water flow.
This work investigates heat transfer quality inside the radiator by applying fins on the inner pipes. Moreover, the standard k-epsilon model and energy equation are used to solve turbulent fluid equations and calculate temperature distribution inside the domain.
Radiator Conclusion
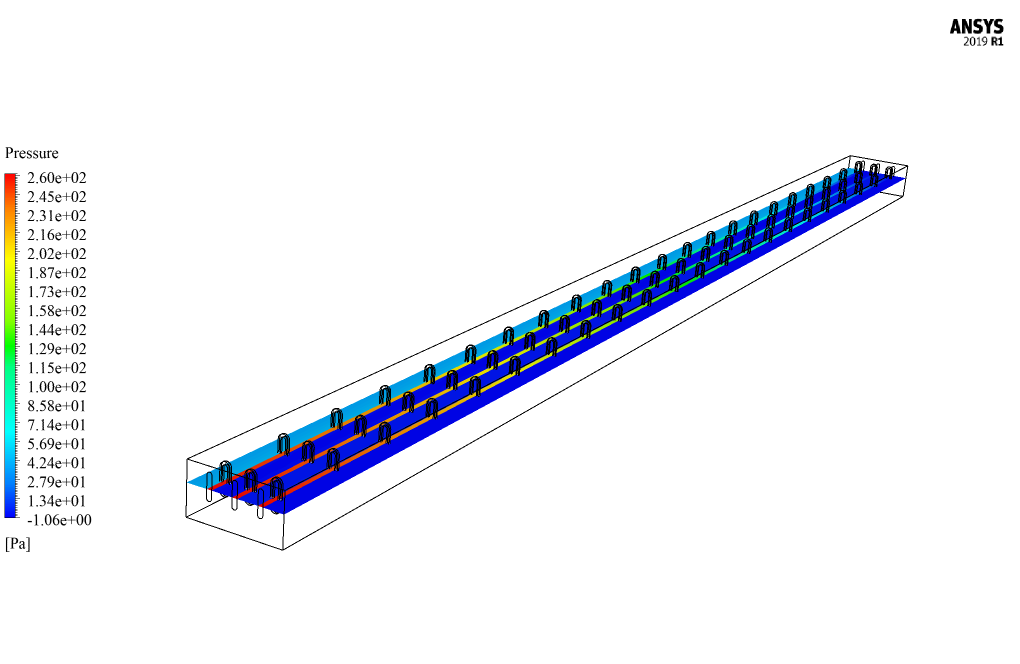
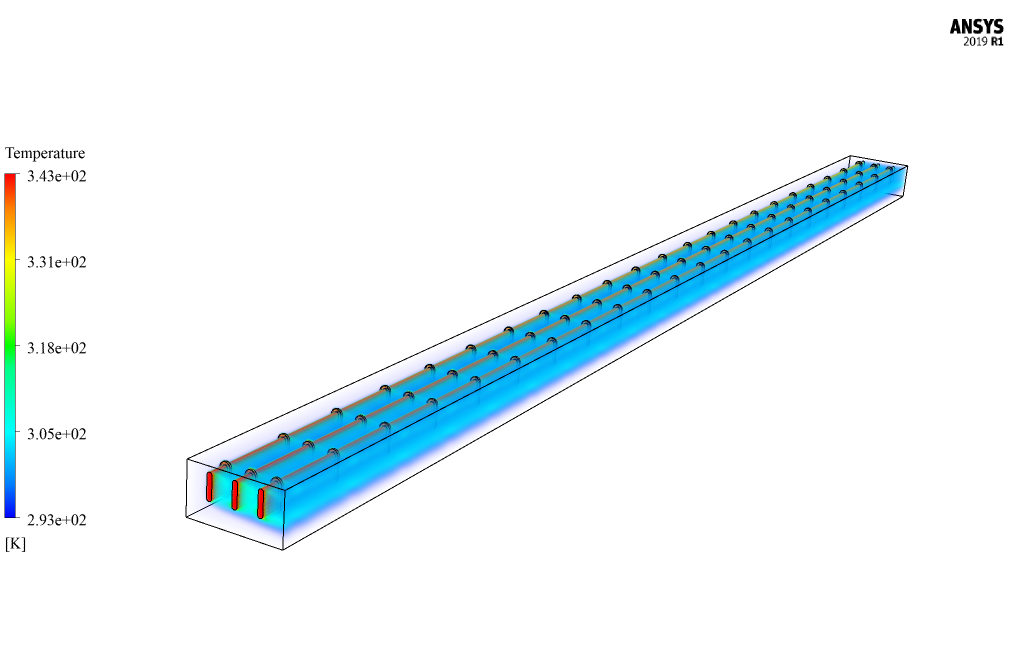
At the end of the solution process, two and three-dimensional contours related to velocity, pressure, and temperature are obtained. The temperature contour shows that the airflow passing over the tubes where hot water flows absorb heat and leaves the domain with a higher temperature.





Cornelius Langworth –
I’m really impressed with the level of detail in the design of this CFD simulation for the finned tube radiator. Your description clearly explained how the addition of fins improves heat transfer—a key aspect of radiator efficiency. Thank you for the dedicated work and thorough investigation through CFD analysis to ensure improvement in heat transfer mechanisms.
MR CFD Support –
Thank you for your positive feedback! We’re glad to hear that our detailed approach and careful investigation of the finned tube radiator’s heat transfer have impressed you. Our goal is to provide insightful and precise CFD simulations to help understand and improve upon these complex processes. Your appreciation motivates us to continue delivering high-quality analyses.
Alycia Watsica –
I just finished going through the Finned Tube Radiator Heat Transfer CFD Simulation, and it was very insightful. It really helped me understand the enhancement of heat transfer using fins. Great learning tool!
MR CFD Support –
We thank you for your feedback on our Finned Tube Radiator Heat Transfer CFD Simulation training course. We’re delighted to hear that you found the course insightful and helpful in understanding heat transfer enhancement techniques. Your satisfaction is our top priority!
Miss Anastasia Waelchi –
This detailed overview of the radiator’s function was incredibly helpful. The explanation of how the fins increase heat transfer by enhancing the contact surface area between the air and water flow solidifies my understanding of the radiator’s efficiency. The use of the k-epsilon model seems ideal for turbulence modeling in this simulation. Overall, I am truly impressed with the thoroughness of the teaching approach and clarity of the CFD concepts demonstrated in this training.
MR CFD Support –
We greatly appreciate your positive feedback! It’s fantastic to hear that our simulation of the finned tube radiator and the educational content met your expectations, providing clear and thorough understanding. We are continually striving to provide high-quality learning experiences and are pleased to know that it reflects in your review. Thank you for taking the time to share your thoughts, and we look forward to delivering more valuable educational simulations in the future.
Trey Bergnaum –
I am amazed at how informative the fins heat transfer simulation results were. Seeing the visual temperature contours really helped me understand the radiator’s efficiency.
MR CFD Support –
We sincerely appreciate your positive feedback on our training for the Finned Tube Radiator Heat Transfer CFD Simulation. It’s delightful to hear that the visual aids effectively conveyed the concepts of heat transfer and radiator efficiency. Thank you for choosing our ANSYS Fluent training products!
Brennon Dibbert –
The detailed simulation of heat transfer inside a finned tube radiator is really fascinating! Its clear the CFD analysis provided by MR CFD thoroughly explores the effectiveness of fins in enhancing heat dissipation. Really appreciate the educational value of this ANSYS Fluent training.
MR CFD Support –
Thank you for the positive feedback! We’re glad you found the finned tube radiator simulation fascinating and educational. MR CFD is committed to providing high-quality and thorough CFD analyses. It’s great to hear that our ANSYS Fluent training proved to be valuable!
Prof. Simone Lubowitz –
I’m amazed by the level of detail in this CFD simulation of a finned tube radiator. The addition of fins to increase the heat transfer efficiency seems like a smart approach. I appreciated learning about the interaction between the hot water and the air and how it effectively transfers heat. The use of the standard k-epsilon model and the energy equation for this process was very insightful. Great work on the project and the comprehensive use of ANSYS Fluent!
MR CFD Support –
Thank you so much for your kind words! We’re thrilled to hear that the simulation was insightful and that you appreciated the detailed explanation and methodology. It’s wonderful to know that the approach we’ve detailed in the training for maximizing heat transfer was clear and made sense to you. Your feedback is immensely valuable to us. If you ever have any more questions or need further assistance with our simulation products, feel free to reach out. Thanks again for taking the time to share your positive experience!
Dr. Florian Rohan I –
I’ve just finished simulating a finned tube radiator using the training material provided, and I was impressed with the clarity of instructions and comprehensive approach taken to guide us through the complete setup, simulation, and results analysis process. The fact that heat transfer was effectively shown with both two and three-dimensional contours made understanding the results much simpler.
MR CFD Support –
Thank you for your positive feedback! We are thrilled to hear that our finned tube radiator heat transfer simulation training has been helpful and easy to understand. We strive to provide clear instructions and comprehensive materials so users can achieve successful outcomes with their simulations. It’s great to know the provided contours aided in a clearer understanding of the heat transfer process. If you have any further questions or need more assistance in your CFD learning journey, don’t hesitate to reach out!
Manuel Ryan –
This tutorial is terrific! It really helped me understand the essentials of simulating a finned tube radiator. I could follow each step, and the results of my simulation were very insightful. Your approach in setting up the mesh and using the k-epsilon model for turbulence was straightforward and practical. Thanks for a great learning tool!
MR CFD Support –
We’re thrilled to hear that you found our Finned Tube Radiator Heat Transfer CFD Simulation tutorial helpful! It’s always our goal to provide clear and practical steps to enhance the understanding of our customers. Should you have any more learning needs in the future, we’ll be here with more resources. Thank you for choosing MR CFD Company’s learning products!
Kellen Metz –
The level of detail in the simulated finned tube radiator was impressive. It really showcased the potent effect of adding fins to the system. By creating additional surface area, the efficiency of heat transfer increased significantly while maintaining a smooth flow of water and air. Everything from the inlet to the exit paths was well executed, purely reflecting real-world thermal systems; accurate speed and temperature settings made the simulation immensely invaluable for thermal management studies!
MR CFD Support –
Thank you for sharing your positive experience with our Finned Tube Radiator Heat Transfer CFD Simulation training. It’s great to hear you found the simulation to be detailed and accurate. We always strive to provide comprehensive and realistic simulations that serve as valuable resources for thermal management study. We look forward to assisting you with any further learning products you may need.
Dr. Fae Hessel MD –
I’m impressed with how detailed the analysis is and how it tackles real-world engineering situations. It’s fascinating to know that engineers can optimize systems before they even physically exist!
MR CFD Support –
Thank you for your kind words! We’re glad to hear you are impressed by the depth of analysis our CFD simulations can provide. At MR CFD, we strive to offer detailed and practical insights to support engineering solutions. Your feedback motivates us to continue delivering high-quality products.
Prof. Jonathan Schmeler V –
I’m completely impressed with how efficient this radiator simulation is. The use of Fins has always been fascinating to me!
MR CFD Support –
Thank you for your positive feedback! We’re glad to hear that you are fascinated by the efficiency gains that fins provide in the radiator simulation. Their ability to increase the heat transfer surface area is a key factor in improving overall performance. If you have more feedback or need further information about simulations, feel free to reach out!
Mrs. Aimee Johns –
The Finned Tube Radiator training was exceptionally informative. The emphasis on practical CFD applications and the ability to visualize the heat transfer was very valuable. Truly impressive course content and structure!
MR CFD Support –
We appreciate your positive feedback on the Finned Tube Radiator heat transfer simulation training! We’re glad to hear our course could effectively demonstrate the practical aspects of CFD analysis and visualization of heat transfer in such systems. Thank you for choosing MR CFD’s learning products!