Population Balanced Model Crystallization CFD simulation
$240.00 Student Discount
- This project numerically simulates the Population Balanced Model Crystallization using ANSYS Fluent software.
- The 2-D geometry is designed in Design Modeler software.
- We used ANSYS Meshing Software to generate mesh; the element number equals 89,244.
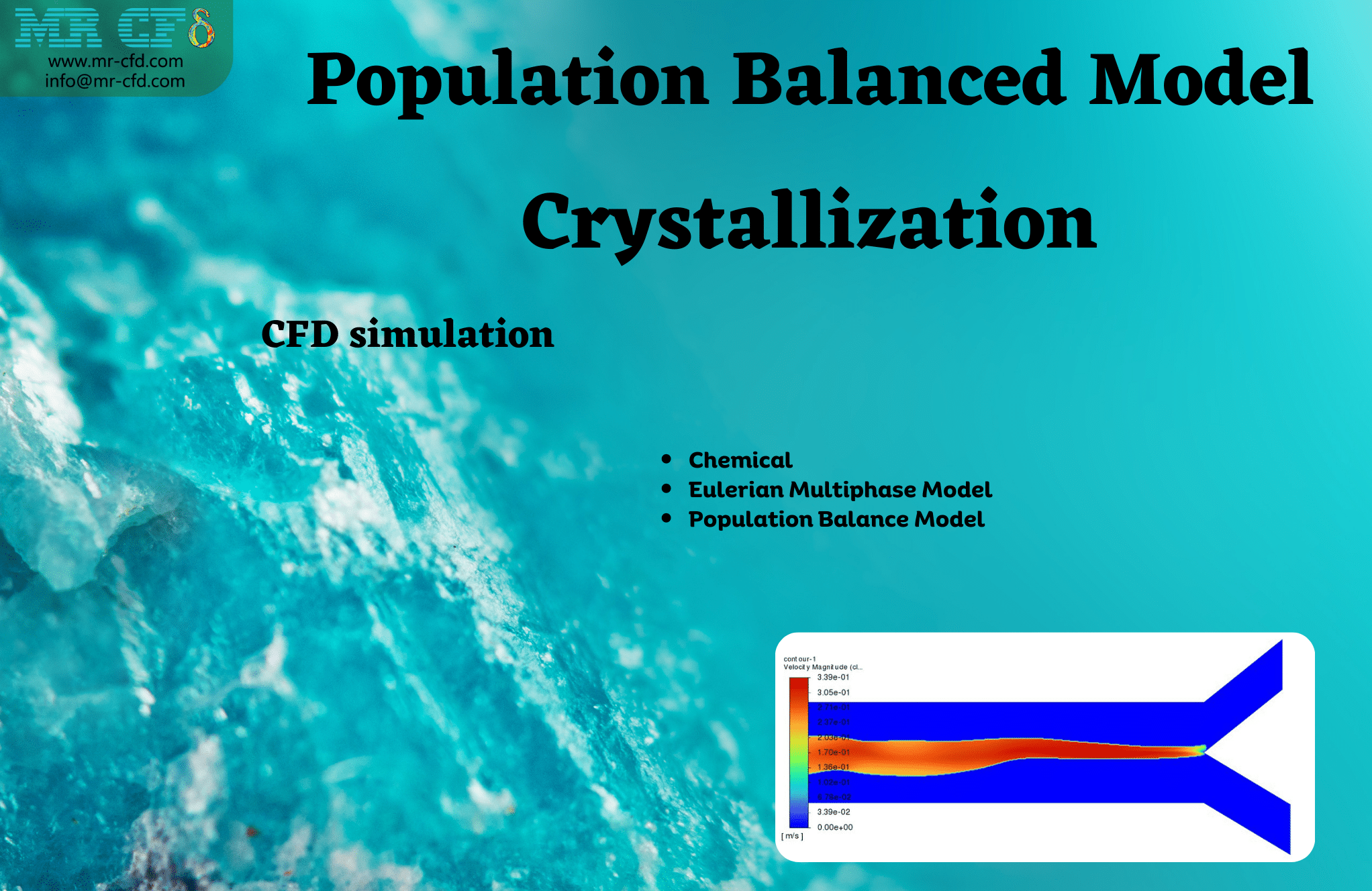
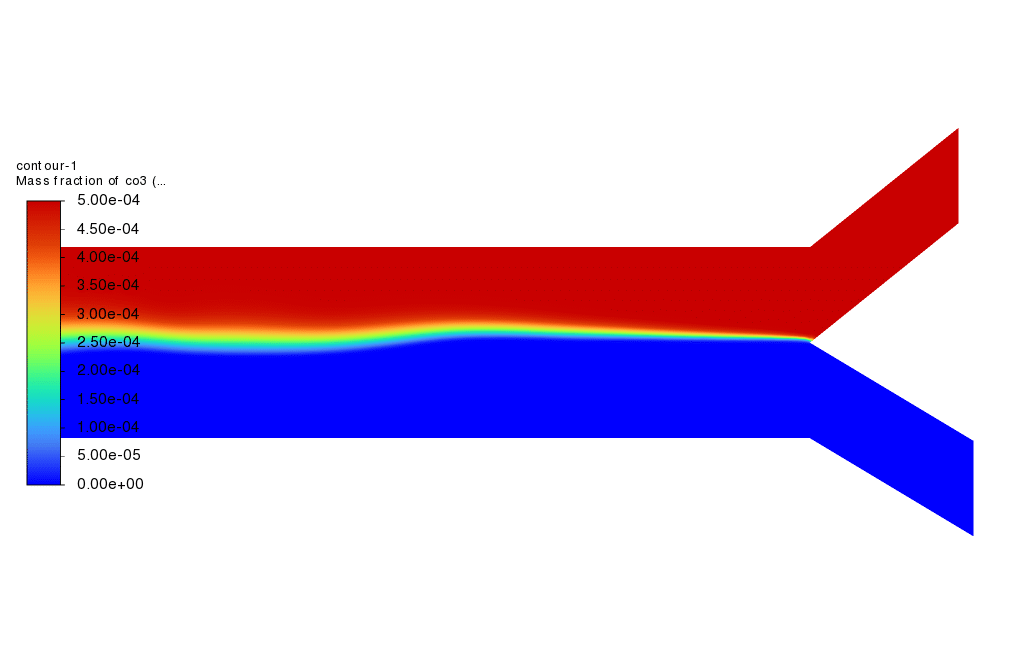
- The multiphase Eulerian multiphase model simulates the mixture (water liquid, Ca, and CO3 ions) and Calcium-Carbonate.
- The crystallization modeling through PBM is also considered.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Population Balanced Model (PBM) Crystallization CFD simulation, ANSYS Fluent Training
Description
The crystallization process is a fundamental phenomenon in which solute particles come together to form a solid crystal structure. Modeling the crystallization process using a population balance model (PBM)is a powerful tool for a detailed understanding of crystal growth, nucleation, and size distribution. It considers super-saturation, temperature, mixing conditions, and impurities. By solving the population balance equation, researchers can simulate and predict the behavior of crystals during the crystallization process.
Modeling the crystallization process using a population balance model provides valuable insights into crystal growth, nucleation, and size distribution. This approach finds applications in pharmaceuticals, chemicals, food, materials science, and energy storage industries. Researchers can optimize product quality, enhance process efficiency, and contribute to advancements in various industrial sectors by understanding and controlling the crystallization process.
The geometry of the present project was designed using ANSYS design modeler and mesh in ANSYS meshing. The mesh type is structured, and the total element number equals 89,244.
Crystallization PBM CFD simulation Methodology
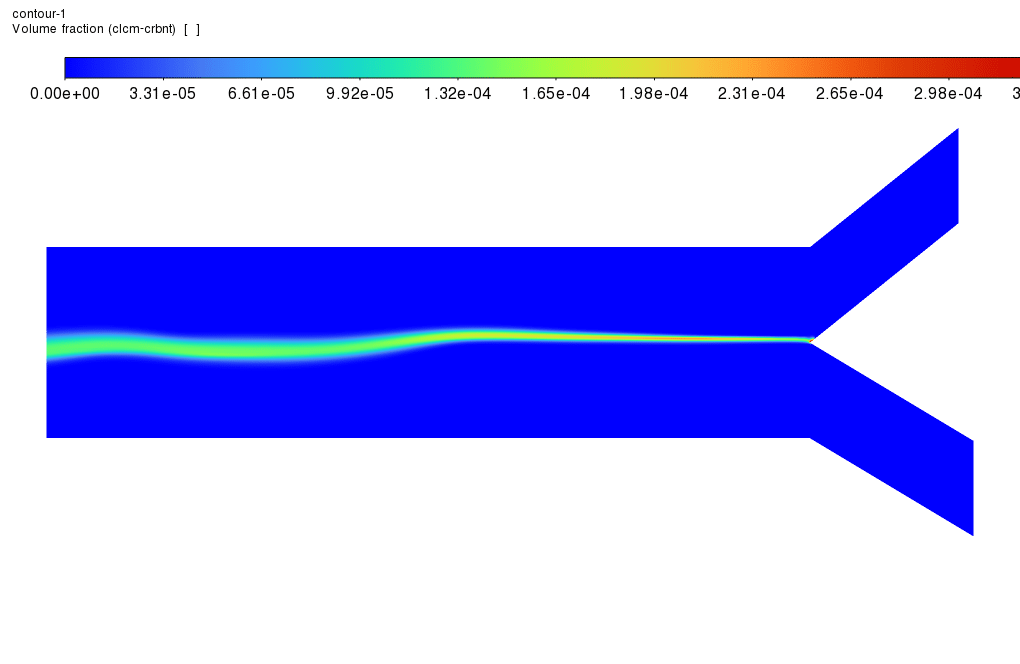
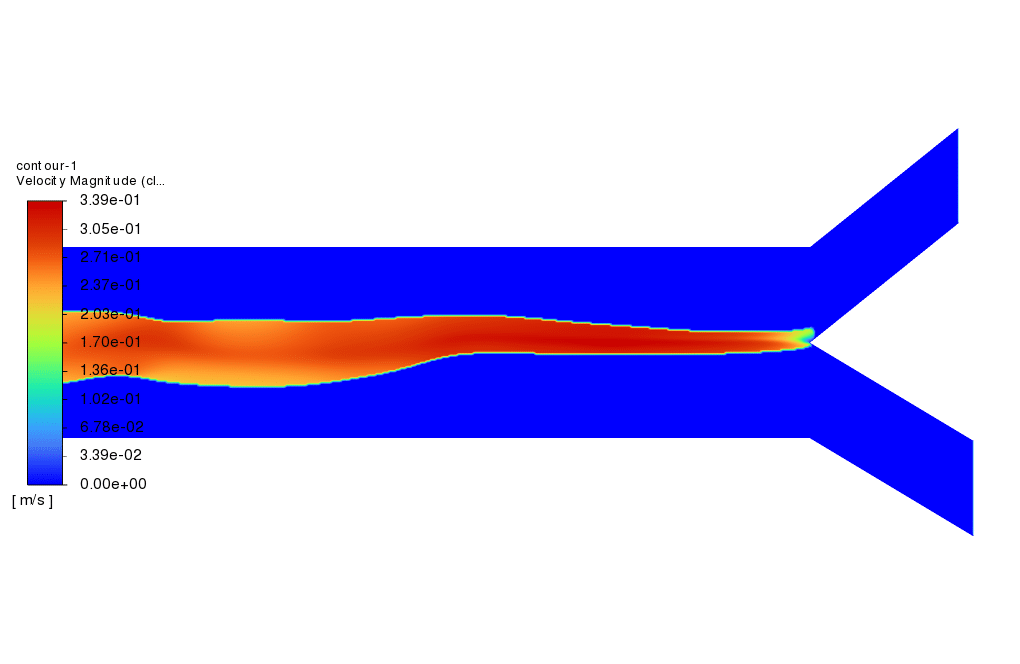
The Eulerian multiphase model was employed in this simulation not only to model the two phases of the mixture (containing water liquid, Ca, and CO3 ions) and Calcium-Carbonate but also to activate the population balance model. Four different classes of bins were considered in this project, with the ratio of exponent set to 1. The minimum diameter was also set to 0.0008 m. Nucleation and growth rates were activated, and constant values of 2e+10 and 2e-11 were set for each one, respectively.
Moreover, the Laminar model was used to simulate the flow equations. 2-D geometry was considered. The present problem is considered complex due to its nature, which includes not only the mixing of different species but also a chemical reaction between two species of Calcium and Carbonate ions. Furthermore, the crystallization modeling through PBM is also considered; activating these models causes the problem to be highly complex. This calls for a multi-stage simulation process. Therefore, three different stages are considered for each mixing, reaction, and crystallization process. The transient study is performed since the PBM model is a time-dependent method.
Conclusion
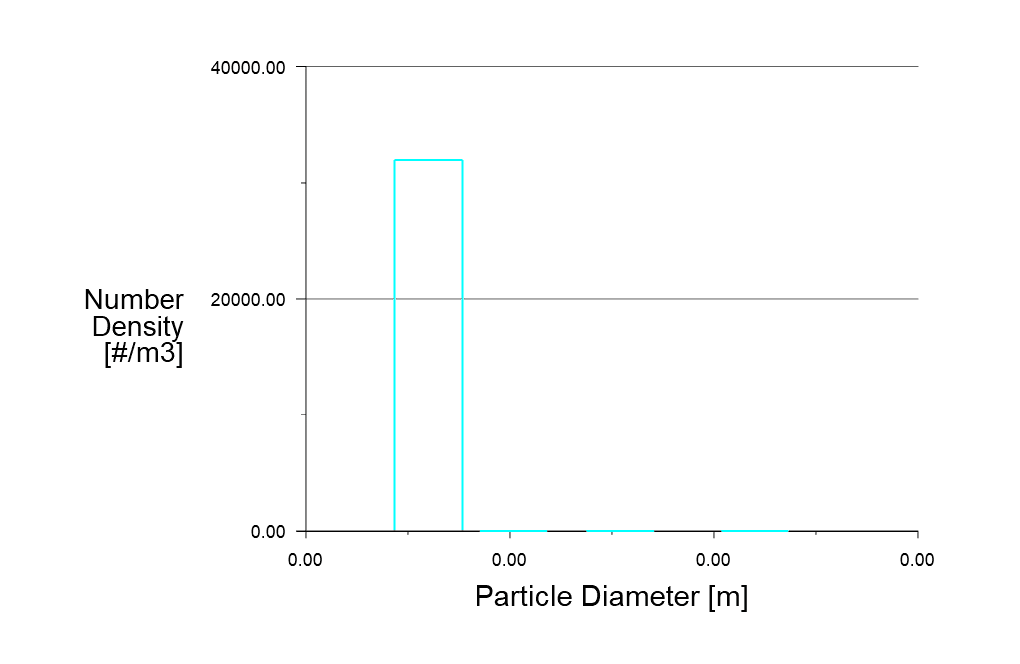
As shown, different contours, including the phases’ velocity inside the domain, distribution of different classes of bins, and changes in a fraction of each bin, are shown. The heterogeneous reaction contour shows that the reaction between the Ca and Carbonate ions occurs precisely over the line where the two ions are mixed. Moreover, suppose the contours of different bin classes are viewed. In that case, one can easily understand how the nucleation and growth phenomena have worked, as the volume fraction of each bin has expanded in the domain, indicating that the solid phase of calcium carbonate has formed. Furthermore, suppose the number density histogram plot is viewed. In that case, one can see that it is possible to increase the number of bins and consider smaller bin sizes, as the value of number density is almost zero. In contrast, the number density of the smallest bin is enormous. This can be interpreted in the way that not all tiny bins and particles are considered. Therefore, considering smaller values for the minimum diameter in the PBM settings can solve this problem.
This video is the 2nd episode of the Population Balanced Model Training Course.












Pearl Christiansen –
This was an excellent training course! The way PBM crystallization was broken down into manageable phases provided a comprehensive overview. I’d be interested to know if this process allows for the consideration of different shapes of crystals, or if it’s limited to specific forms due to the complexity of the simulation?
MR CFD Support –
In this simulation, the PBM crystallizes the course mainly focused on the size distribution and growth rates of crystals. While the model typically considers spherical crystals, for more complex shapes, additional parameters and advanced modeling techniques would be necessary to accurately represent their formation and behavior.
Felton Mraz –
As an engineer interested in optimizing the process, could it be possible to adjust the initial supersaturation level in my CFD model to see its effect on crystal size distribution?
MR CFD Support –
Absolutely, you can adjust the initial supersaturation level within the CFD model to study its effect on the crystal size distribution. This would involve altering the initial concentrations or the operating conditions that dictate the supersaturation within the simulation setup. By doing so, you can observe how changes in supersaturation influence nucleation rates and crystal growth, thus impacting the overall size distribution of the crystals.
Ian Bauch –
What does the Population Balance Model (PBM) provide in terms of analysis for the crystallization process?
MR CFD Support –
The Population Balance Model (PBM) provides a comprehensive analysis of the crystallization process by calculating the crystal size distribution, nucleation rate, and growth kinetics. You can use this model to capture the dynamics of the crystallizing system and forecast the quality of the final product based on the operating conditions in the simulation.
Camron Hauck Sr. –
Wonderful learning product! The PBM Crystallization CFD simulation training was insightful and comprehensive. It provided a detailed explanation of crystal growth and nucleation patterns to predict the crystallization behavior effectively. The ANSYS software integration and practical examples made it genuinely applicable to real-world scenarios. Great work by MR CFD Company!
MR CFD Support –
Thank you for the positive feedback on our PBM Crystallization CFD simulation training! It is our aim to provide valuable insights and practical knowledge to our users. We are pleased to know that the course met your expectations and that you found the real-world applications beneficial. Should you have any more questions or need further assistance with our learning products, don’t hesitate to reach out!
Liliane Renner –
Is it possible to adjust the number density histogram plot by considering smaller values for the minimum diameter in the PBM settings? What impact would this have on the simulation results?
MR CFD Support –
Admin Response: Yes, it is possible to adjust the number density histogram plot by considering smaller values for the minimum diameter in the Population Balance Model (PBM) settings. Doing so would allow more fine-grained calculations of the crystal size distribution, including the formation of smaller particles. This could potentially lead to more accurate simulation results, representing the actual crystallization process more precisely, which is particularly important for processes where the size distribution of the crystals is critical.
Gregg Goyette –
The explanation was comprehensive, but I’m curious about what kind of post-processing was done to examine the crystal size distribution in the simulation. Could you provide details on that?
MR CFD Support –
In the post-processing phase of this crystallization CFD simulation, the crystal size distribution was examined using contours for different classes of bins and histograms for number density. The simulation output includes the distribution of crystalline material in the domain, representing the nucleation and growth of crystals over time. By reviewing these distributions and number density plots, researchers can analyze the effectiveness of the nucleation and overall crystal growth in the modeled process. It helps ensure the size and quality of crystals meet the necessary specifications for the intended applications.