Conical Solar Collector CFD Simulation, ANSYS Fluent
$120.00 Student Discount
- In this project, heat transfer in a conical solar collector was simulated using ANSYS Fluent.
- The geometry was created in SpaceClaim, and a mesh consisting of 2,948,101 elements was generated using ANSYS Meshing.
- The Discrete Ordinates (DO) model was chosen to simulate radiation (solar ray tracing model).
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Conical Solar Collector Project Description
Solar energy is the largest source of energy in the world. This energy is clean, cheap, and endless and can be found all over the world. Solar water heaters work by absorbing solar energy from collector plates, and their heating efficiency varies by type of collector. To provide hot water during the day and the night, hot water is kept in a double-sided reservoir with thermal insulation that can keep the water temperature for up to three days without any changes in its temperature.
In this project, heat transfer in a Conical Solar Collector CFD Simulation containing water fluid is carried out and analyzed by ANSYS Fluent software. The cubic computational domain consists of an air inlet (velocity inlet type, 1m/s) and a pressure outlet. The conical collector consists of an water inlet (inlet velocity, 0.01 m/s) and a pressure outlet. It also has 1 layer of glass and 1 layer of steel to decrease convection heat transfer as much as possible. The conical solar collector absorbs the sunlight and warms the water inside its tank.
The geometry for analyzing this simulation consists of a fluid domain and a conical solar collector. The geometry is designed in SpaceClame® and is meshed in ANSYS meshing®. The mesh type used for this geometry is unstructured and the element number is 2948101.
Methodology
The energy and radiation model (solar ray tracing model with DO model) are activated and the k-ε model with the use of standard wall function is exploited for fluid flow analysis.
Results of Conical Solar Collector
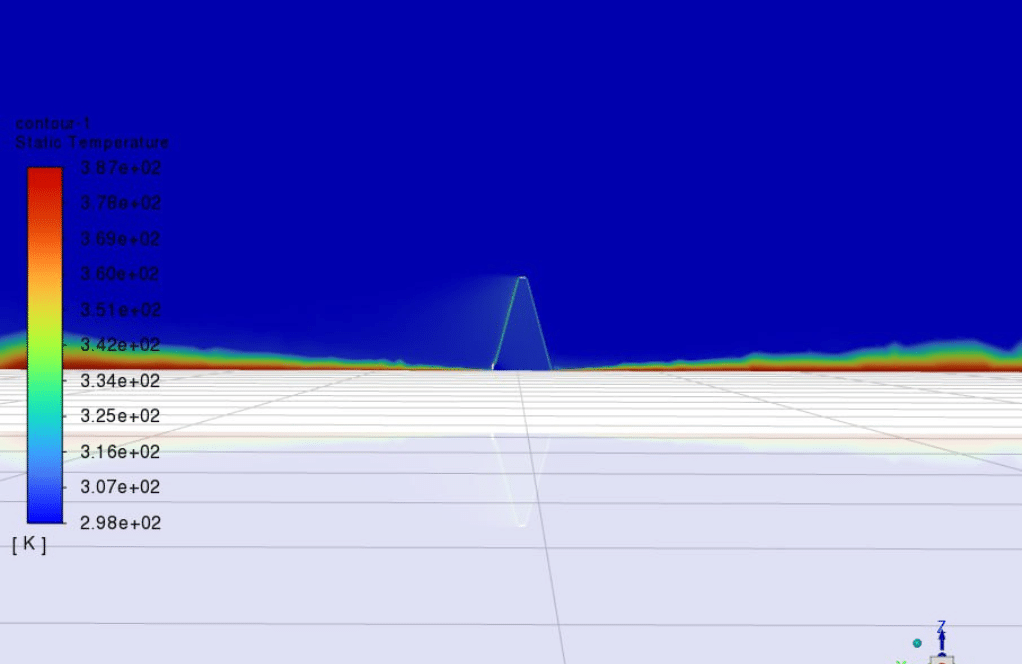
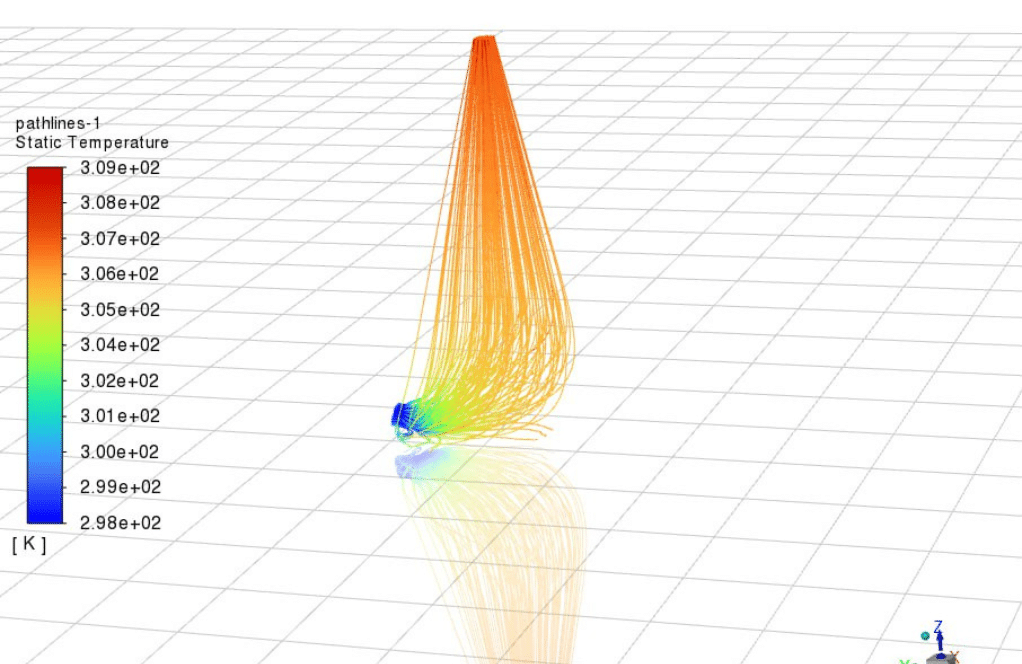
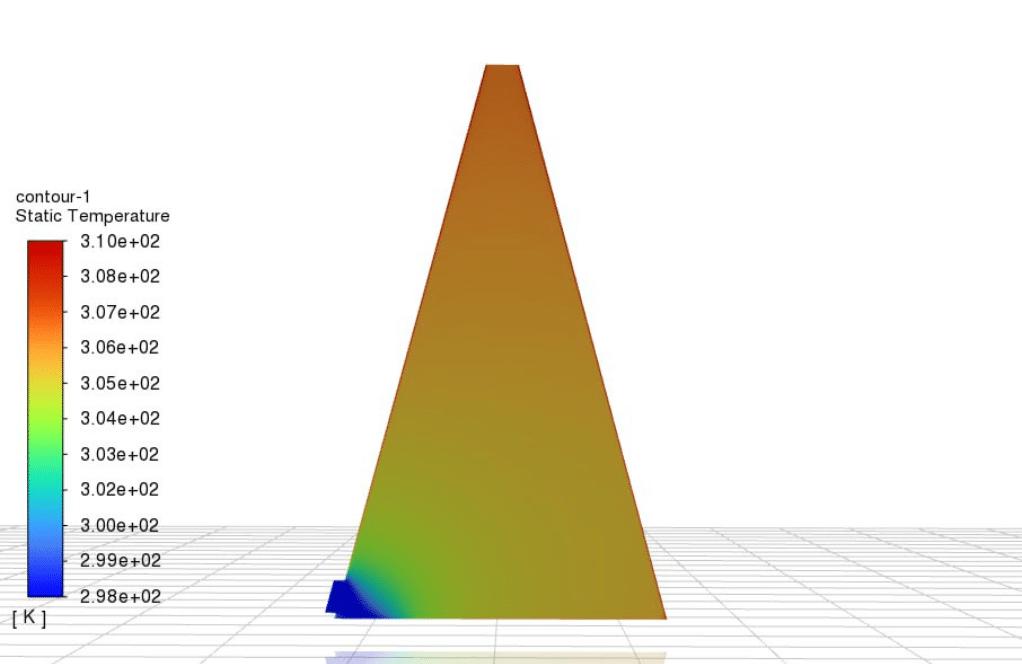
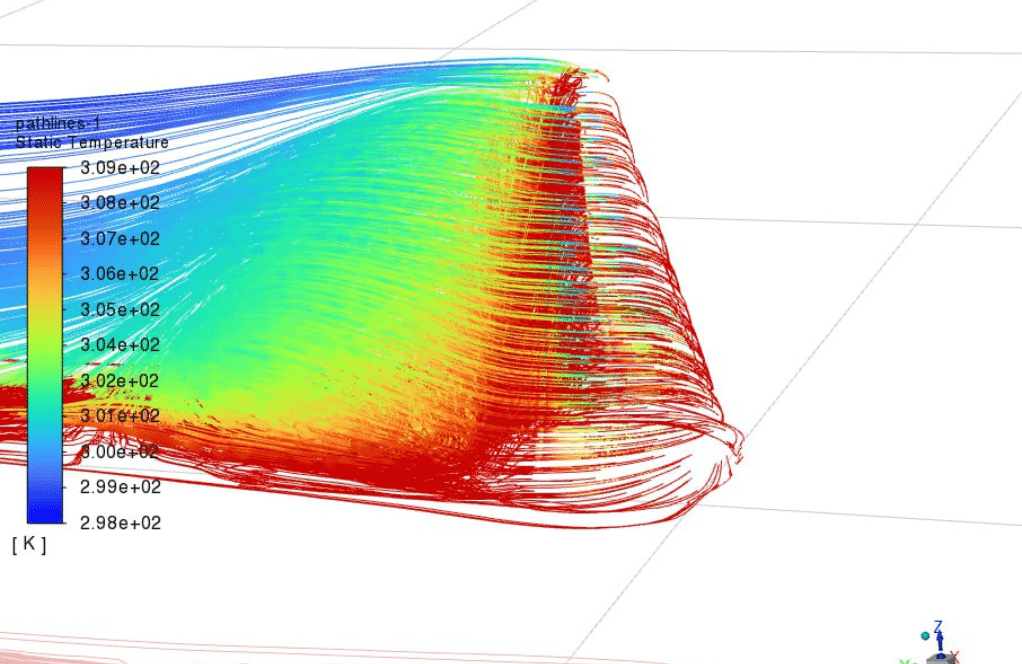
Contours of velocity, temperature, streamlines are presented.
The average temperature of the collector walls reaches 308.67 K, and the water that enters the collector at a temperature of 298.15 K is warmed up inside the collector, with an outlet temperature of 306.8 K.
Total heat transfer through the collector wall is 773 watt.




Mekhi Halvorson –
Can this simulation be customized to model different types of solar collectors and operating conditions?
MR CFD Support –
Yes, we can accommodate your desired simulations. Please share more details about your specific requirements.
Arden Jacobi –
How does the simulation model the solar energy collection process?
MR CFD Support –
The simulation uses the Discrete Ordinates (DO) radiation model to accurately simulate the solar radiation and its interaction with the conical collector.
Hayden Ritchie –
This simulation is a testament to the power of computational fluid dynamics!
Vivien Gibson –
This is an invaluable resource for anyone working in the field of solar energy collection.
Isac Waelchi –
I’ve finished the Conical Solar Collector CFD simulation course, and the outcome was impressive. The detailed analysis and presentation of the temperature variations within the collector helped me understand the efficiency of the design. Well done on the comprehensive educational material!
MR CFD Support –
Thank you for your positive feedback! It’s great to hear that you found the simulation course on the Conical Solar Collector informative and helpful. We’re glad we could assist in enhancing your understanding of solar collector efficiency and temperature analysis. If you have any more questions or need further assistance, feel free to reach out.
Helga Parker II –
I am amazed by the detail of this simulation design! Can we know at what time of the day the simulation represents for the solar intensity?
MR CFD Support –
Thank you for the kind compliment on the Conical Solar Collector CFD Simulation! The specific details about solar intensity would typically correspond to peak solar conditions, like midday sunshine, as the simulation aims to capture the highest efficacy of the solar collector. However, without DIRECT mention of time in the data provided, one cannot conclusively specify the time of day for this scenario.
Kenna Mayer –
I’m thoroughly impressed with how the Conical Solar Collector CFD Simulation performs. Seeing the tangible improvements in water temperature from inlet to outlet due to the effective design is remarkable. The utilization of the solar ray tracing and DO model in ANSYS Fluent has clearly played a crucial role in achieving the high heating efficiency.
MR CFD Support –
Thank you for your positive feedback! We’re delighted to know that the efficiency and detailed results of the Conical Solar Collector CFD Simulation have met your expectations. It’s our goal to provide simulations that not only elucidate complex processes but also demonstrate the potential for real-world applications and improvements in energy systems. If you have any more questions or need further information, don’t hesitate to reach out!
Ignacio Howell –
I am utterly fascinated by how the conical solar collector simulation models the real-life conduction and radiation effects. Higher temperatures achieved by water is especially impressive. Just goes to show the efficiency and utility of the simulation in optimizing solar collector designs!
MR CFD Support –
Thank you so much for your kind words on the Conical Solar Collector CFD Simulation. We are extremely pleased to hear that the results have impressed you and that you find the simulation a valuable tool for understanding and enhancing solar collector systems. If you need any further assistance or have more insights to share, please feel free to reach out!
Bernhard Schuppe –
Kudos to the MR CFD team! I successfully completed my Conical Solar Collector CFD project using your ANSYS Fluent simulation product. The step-by-step guidance made it easy to set up the energy and radiation models. Observing the water temperature rise from the inlet to the outlet was truly satisfying. Your detailed methodology helped me understand the functionality of each simulation parameter. The inclusion of different material layers in the collector’s design to reduce convective heat loss was an insightful touch.
MR CFD Support –
We’re thrilled to hear that you had a great experience with our Conical Solar Collector CFD simulation product! It’s great that the guidance provided was helpful in setting up your project successfully. Thank you for acknowledging the detailed methodology. We believe that understanding the subtleties of simulation parameters is key for successful CFD analysis. Your acknowledgment motivates us to continue delivering high-quality simulation solutions. Thank you for choosing MR CFD!
Derick Kshlerin –
The conical solar collector simulation results indicate improved heating efficiency. The design details and analysis are comprehensive, with clear illustrations of the temperature increase and heat transfer. Well done on effectively leveraging the DO radiation model coupled with the k-ε model to optimize solar energy absorption. The simulation outputs, such as temperature distribution and flow patterns, give valuable insights into the collector’s performance. This project exemplifies skilled CFD application in renewable energy technology and fills me with confidence in MR CFD Company’s learning products.
MR CFD Support –
Thank you for your positive feedback! We are delighted to hear that our Conical Solar Collector simulation was able to convey the complex details in a comprehensive way and that you found the results insightful. MR CFD is committed to providing high-quality and educational simulations that aid understanding and application of CFD in renewable energy. Your satisfaction with the learning products motivates us to continue delivering valuable and actionable knowledge to our customers.