Heater Applied for a Room HVAC, CFD Simulation
$80.00 Student Discount
- The present problem simulates heat transfer by a heater (radiator) inside a room by ANSYS Fluent software considering HVAC analysis.
- We carry out the present 3-D model using the Design Modeler software.
- The meshing of the room and the heater is done using ANSYS Meshing software and the mesh type is structured. The element number is 87865.
- Considering natural convection and buoyancy effect.
Click on Add To Cart and obtain the Geometry file, Mesh file, and a Comprehensive ANSYS Fluent Training Video.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Heater Applied for a Room HVAC, ANSYS Fluent CFD Simulation Training
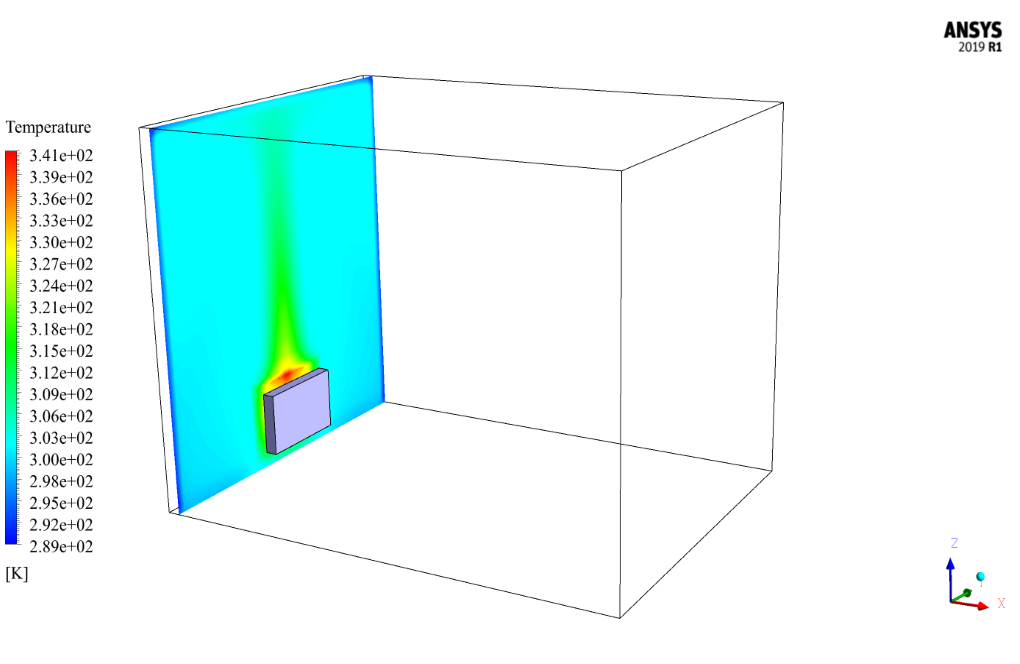
The present problem simulates heat transfer by a radiator inside a room using ANSYS Fluent software. In fact, the heater is connected to one of the sidewalls of the room, which acts as a heat source, and its body has a constant thermal flux equal to 1886.792 W/m2.
The sidewalls and ceiling have a thickness of 0.2 m of wood, which has convection heat transfer with the outside; Thus, the ambient air temperature is assumed to be 280 K and the convection coefficient is assumed to be 10 W/m2K.
The purpose of this study is to investigate the heat transfer rate from the heater to the interior of the room using the natural convection and buoyancy effect.
Therefore, the gravity force is applied to the model. We carry out the present 3-D model using the Design Modeler software. The meshing of the room and the heater is done using ANSYS Meshing software and the mesh type is structured. The element number is 87865.
Methodology
The energy model is activated to analyze heat transfer.
Conclusion
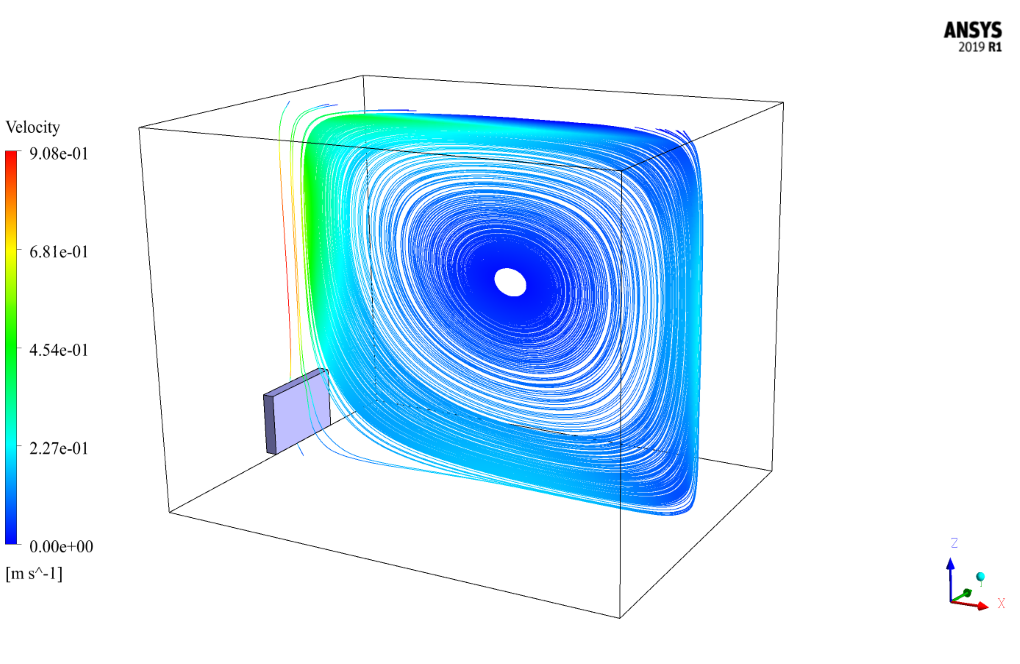
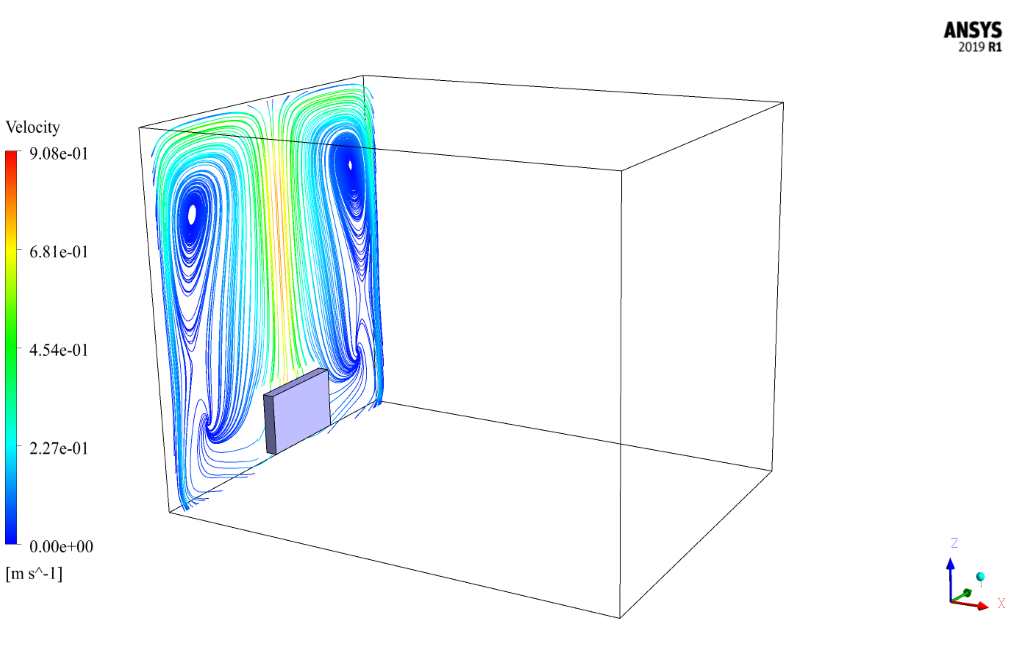
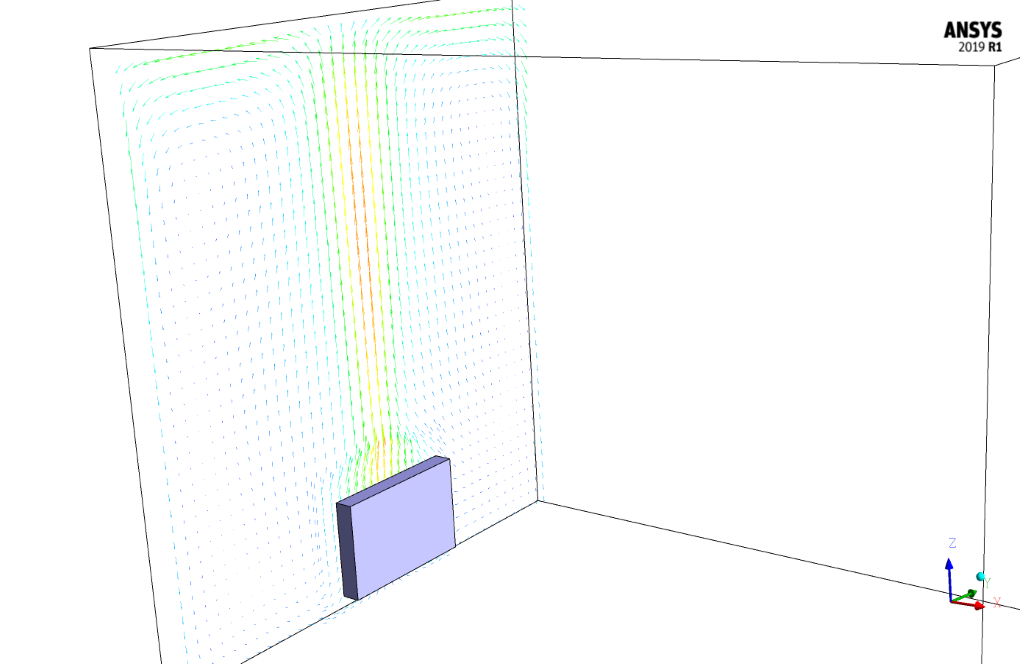
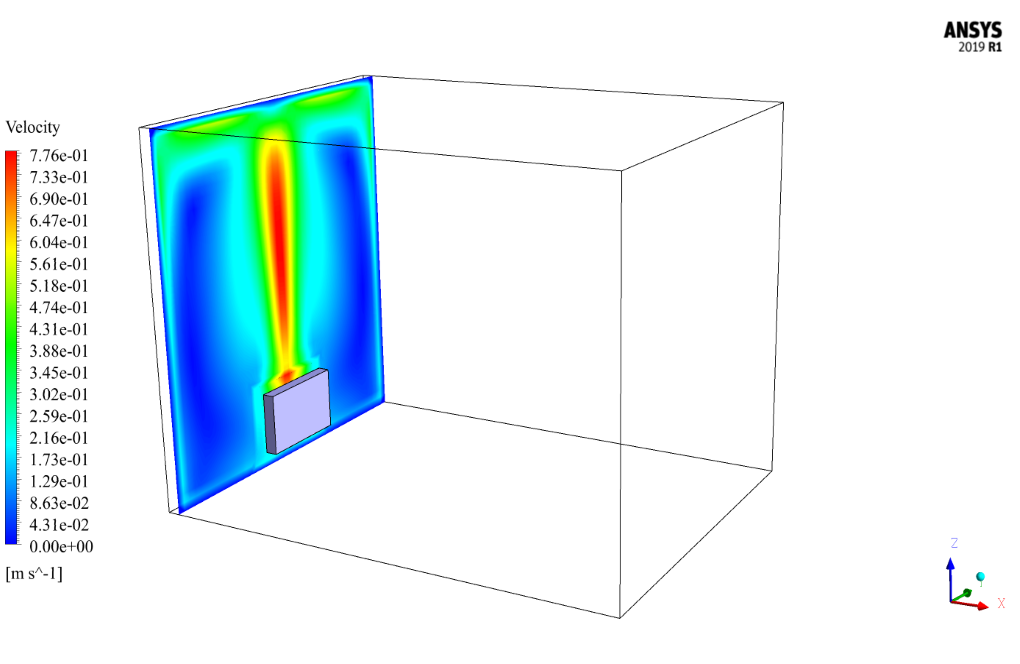
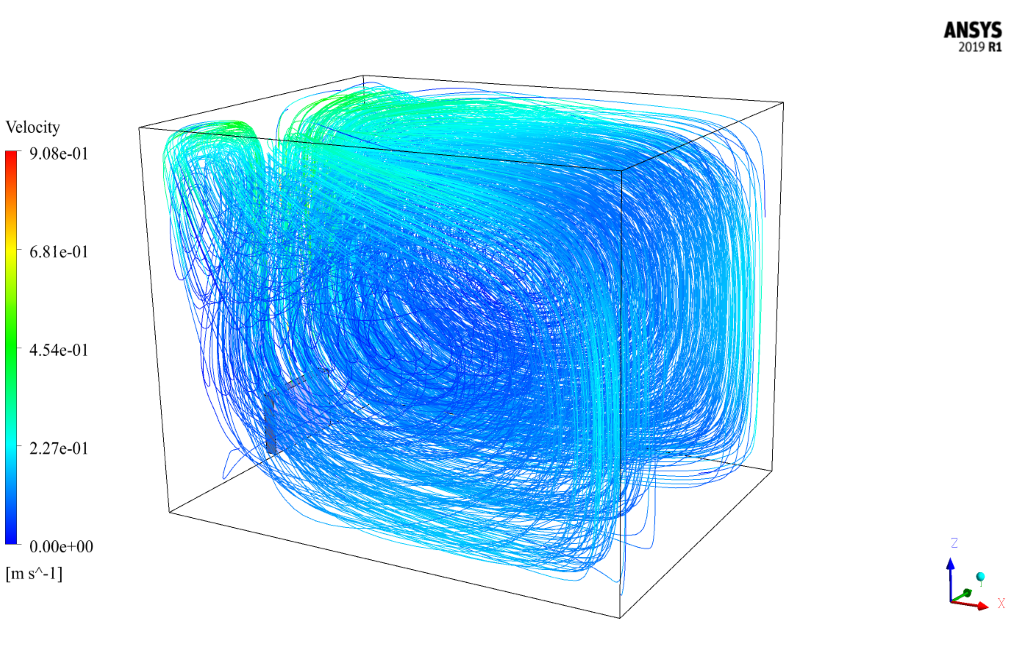
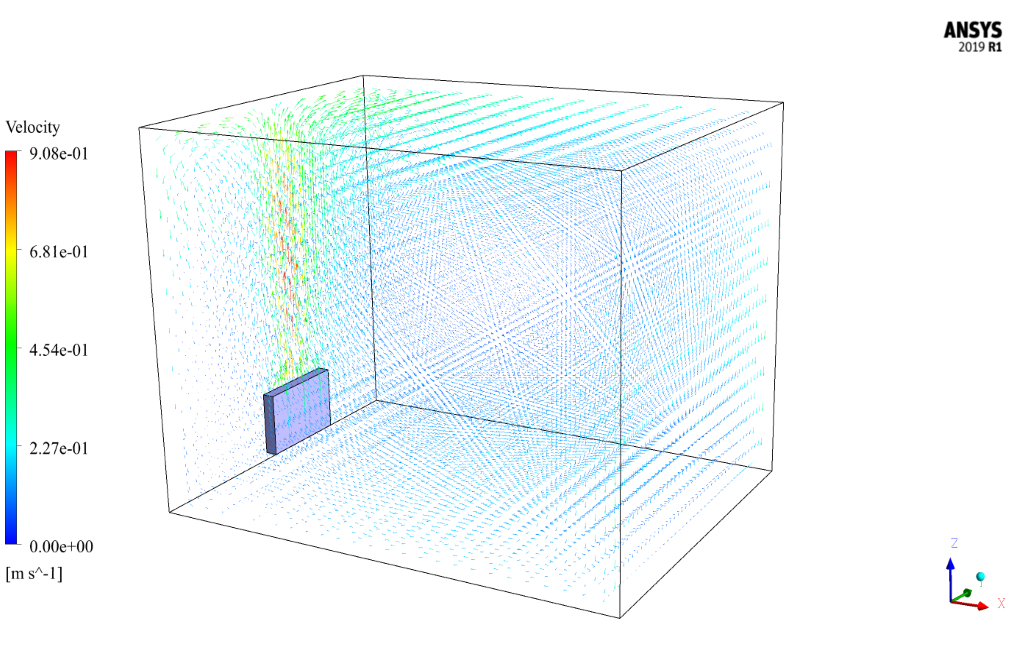
At the end of the solution process, the velocity, temperature, pressure contours, pathlines, and velocity vectors all two-dimensional and three-dimensional, are obtained.
As can be seen from the contours, the presence of the radiator was able to increase the temperature in the room to some extent. This increase in temperature and the resulting increase in velocity is more pronounced near the walls and especially near the radiator installation site.




Sandy Sipes –
Your job is right MR-CFD
Aileen Langworth Jr. –
Your Room Single Side HVAC Using a Heater CFD Simulation product is very detailed!
Kaylin Harvey PhD –
The quality of your simulations is impressive!
MR CFD Support –
We appreciate your kind words! We continually strive for excellence in all our simulations.
Mr. Brennon Turner –
I’m thrilled with the detailed analysis on temperature and velocity changes due to the radiator. Your simulation clearly shows the effectiveness of room heaters on ambient temperature!
MR CFD Support –
Thank you for sharing your positive experience with our Heater Applied for a Room HVAC CFD Simulation training! It’s great to hear that the results of our detailed analysis provided useful insights on temperature moderation using a radiator. We appreciate your feedback and are glad that our product met your expectations.
Prof. Kayley Johnston Sr. –
After going through the learning materials on the heater HVAC simulation, I’ve seen improvements in my understanding of natural convection heat transfer. The visuals provided by the velocity and temperature contours really helped solidify my grasp of the concepts. Great job!
MR CFD Support –
Thank you for your positive feedback! We’re delighted to hear that our training materials have enhanced your understanding of HVAC systems and natural convection. It’s always encouraging to know that the visuals and simulations we provide are effective for learning. If you have any further questions or need additional support, please don’t hesitate to reach out!
Bernie Mante Sr. –
I was impressed with how effectively the radiator could increase the room temperature in your simulation. I am planning on recommending the training to a colleague interested in HVAC design.
MR CFD Support –
Thank you for your kind words and for considering our training valuable enough to recommend. We are delighted to hear that the simulation results were impressive and useful for your understanding of HVAC systems. Your feedback is greatly appreciated, and we hope your colleague will find our training just as beneficial!
Maude Kutch –
I was really impressed with the way the natural convection and buoyancy effects have been studied through this simulation. The detail in heat transfer from the heater is incredible, and the visual outputs are quite enlightening!
MR CFD Support –
We’re very pleased to hear you found the simulation enlightening and that it met your expectations for studying natural convection and buoyancy effects. We always aim to provide detailed visual outputs to enhance understanding. Thank you for your positive feedback!
Dewitt Stroman –
Extremely satisfied with the HVAC CFD Simulation training. It was incredibly beneficial to see the temperature distribution changes caused by the radiator. The visuals really helped in understanding the buoyancy effect on heat transfer within the room.
MR CFD Support –
Thank you for your kind words! We’re thrilled to hear that you found the training helpful and the visual representations beneficial for grasping the concepts. Our goal is to provide clear and educational simulations that enhance understanding, and it’s great to see this was achieved with the HVAC CFD Simulation. If you need any further assistance or have more questions, don’t hesitate to reach out.
Libby Daniel –
I am absolutely thrilled with the detailed analysis provided in this CFD simulation of a room HVAC system. The representation of the natural convection as heat is transferred from the heater across the room is impressive, and the inclusion of gravity strengthens the realism of the simulation. Understanding the effect of heater placement on the temperature distribution is crucial for optimized HVAC design, and this training module delivers just that. Great job at visualizing the temperature gradients and velocity profiles!
MR CFD Support –
Thank you so much for your positive feedback! We are delighted to hear that you found the HVAC simulation training module useful and that it gave you a clear visualization of heat distribution and air flow in a room with a radiator. We strive to provide comprehensive and realistic simulation scenarios that can aid in better HVAC system design. Your satisfaction is very rewarding for us, and we look forward to providing you with more valuable learning experiences in the future.