
Y+ and Grid Types
What is Meshing in ANSYS?
grid means converting the computational domain to smaller subdomains to solve momentum, turbulence, and energy equations and finally obtain results for all levels of the simulated model.
Introduction
It is critical to creating a high-quality mesh to find dependable solutions and ensure numerical stability. Mesh generation, also known as grid generation in the CFD world, has evolved into its field and is still a very active area of study and development. Many existing commercial codes on the market have robust built-in mesh generators and various independent grid generating packages, demonstrating this. For the first time, creating a mesh is a daunting task, requiring judgments on the placement of discrete points (nodes) throughout the computational domain and the type of connections for each point. The mesh quality determines the success or failure of the numerical simulation.
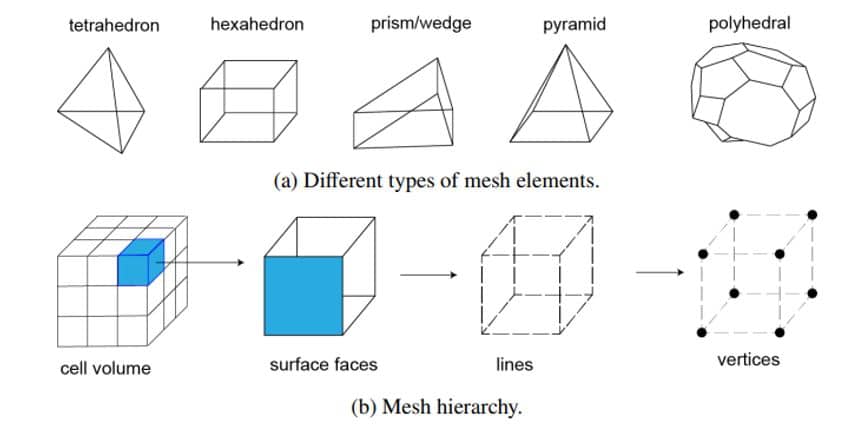
Figure (a) shows mesh elements are Tetrahedron, hexahedron, prism/wedge, pyramid, and polyhedral. (b) Mesh topology shows the meshing hierarchy at each level.
Mesh Generation
Mesh generation divides a continuous geometric space into discrete geometric and topological cells to form a mesh. These cells frequently form a simplicial complex. We usually partition The geometric input domain by the cells. Mesh cells utilizes to approximate the bigger domain in a discrete local manner. Depending on the complexity of the domain and the type of mesh sought, it uses computer algorithms to produce meshes, which humans often guide via a graphical user interface (GUI). A common aim is to generate a mesh that precisely replicates the input domain geometry while having high-quality cells and not having too many cells to make subsequent calculations intractable. The mesh should likewise be fine in critical places for the following calculations (small elements).
We can use Meshes to generate a computer screen and simulate physical processes such as finite element analysis and CFD. Also Meshes made up of primary cells like triangles so that we can conduct operations on them like finite element calculations (engineering) and ray tracing (computer graphics).
Cell shapes that are commonly encountered.
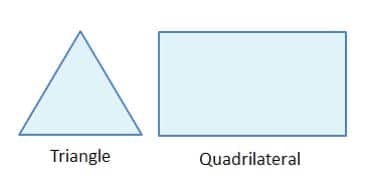
Two-dimensional
The most frequent two-dimensional cell shapes are rectangles and squares. The triangle and the quadrilateral are these shapes.
Triangle
This cell has three sides and is one of the most basic mesh shapes.
Quadrilateral
This cell has a basic four-sided shape, as shown in the diagram. It’s most frequent in grids with a defined structure.
Three-dimensional
The basic three-dimensional elements are the tetrahedron, quadrilateral pyramid, triangular prism, and hexahedron. There are triangular, and quadrilateral faces on all of them.
Tetrahedron
A tetrahedron comprises four vertices, six edges, and four triangular faces. We can create a tetrahedral Volume Mesh automatically in most circumstances.
Pyramid
Five vertices, eight edges, four triangular and one quadrilateral faces make up a quadrilateral pyramid. In hybrid meshes and grids, these work well as transition elements between square and triangle-faced elements and other elements.
Triangular prism
A triangular prism make up of six vertices, nine edges, and two triangular and three quadrilateral faces. This type of layer has the advantage of efficiently resolving boundary layers.
Hexahedron
A hexahedron, sometimes known as a topological cube, has eight vertices, twelve edges, and six quadrilateral faces. It refer sometimes to as a hex or a block.
The accuracy of solutions in hexahedral meshes is the highest for the same cell amount.
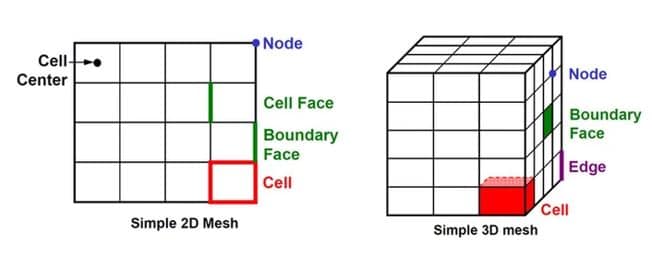
Grid/Mesh
A mesh is a tool that separates a shape into several parts. The CFD Solver uses these to create control volumes.
Terminology:
- Cell = control volume into which domain is broken up.
- Node = grid point.
- Cell center = center of a cell.
- Edge = boundary of a face.
- Face = boundary of a cell.
- Zone = grouping of nodes, faces, cells
- Domain = group of node, face, and cell zones.
Types of Meshes in ANSYS
The meshing in ANSYS Fluent is structurally divided into two parts:
Structured mesh
Unstructured mesh
Structured Meshes
In a Structured mesh, each element can be addressed with a row and column number because, in a Structured mesh, the mesh is produced in a completely regular manner. In contrast, this is practically impossible in an Unstructured mesh due to the lack of order in creating the mesh.
Unstructured mesh
Unstructured CFD meshing technologies have evolved, and commercial CFD suppliers increasingly use them. They give the user more automated options for creating a mesh model and a user-friendly interface.
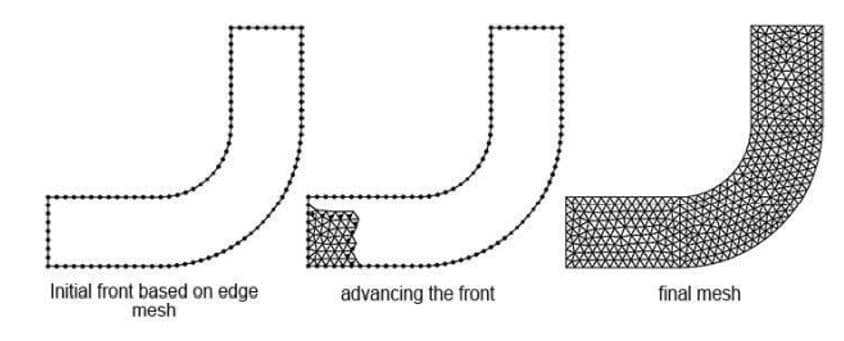
The standard method for creating an unstructured mesh includes the following steps:
– detecting the edges of a surface and creating nodes to construct the boundaries of each surface
– creating additional nodes on the surface and connecting them to fill the surface with data
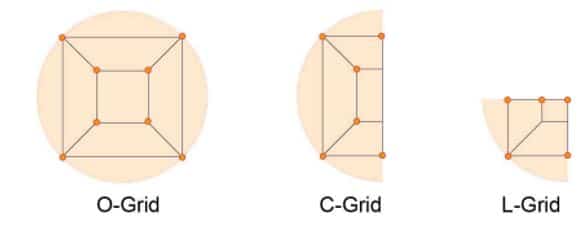
An O-grid consists of lines of points with the last point wrapping around and meeting the first, forming a circular ‘O’ shape. A C-grid, for example, has lines that bend in a semicircle shaped like a letter ‘C’ (basically half of an O-grid), but an L-grid has lines that bend in an L-shape formed from a quarter of an O-grid.
The following figure shows several examples.
It takes a long time to create structured meshes for complicated geometries since it requires a lot of manual labor. Unstructured tetrahedral, hexahedral, and polyhedral meshes are employed as a result. Unstructured meshes benefit from being more adapted to fitting into complicated forms. Furthermore, volume filling may be done automatically using a Delauney triangulation or a hierarchical technique. On the other hand, Tetrahedrons tend to get overstretched in areas with high curvatures, resulting in high aspect ratios that influence the skewness of the cells; this is not the case with hexahedral cells. Additionally, aligning tetrahedral cells with the flow direction might be problematic. These two issues can stymie convergence and cause numerical diffusion or manufactured mistakes in the solution.
Polyhedral Meshing
These elements, which have grown more popular, are an alternative to tetrahedral meshes. Polyhedral have a higher number of near surrounding cells than tetrahedra, which is a significant benefit (typically ten, compared to four for tetrahedra). This gives gradient approximations more resolution. Polyhedral cells are formed by merging tetrahedral cells. As a result, the total cell count is lowered, as are severely skewed cells. Because of their uneven form, polyhedral cells are less susceptible to stretching. Polyhedral meshes need additional computing operations per cell due to the higher number of nodes and faces per cell and the increased number of neighbors. However, the short time to convergence compensates for this.
What is Y-Plus (Y+)?
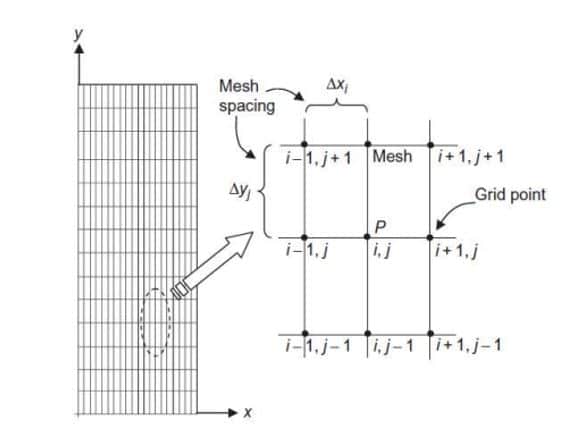
The application of wall functions, which derive the shear stress at the wall from semi-empirical equations, is one way to describe the solution of the shear stress at a wall. The dimensionless variable y-plus represents the distance from the wall to the first grid cell’s center.
Also, Y-plus is a distance with no dimensions. In other words, Y-plus renders the vertical space between the element’s center and the wall dimensionless. This value is used to evaluate the proportionality of the grid element’s size (height) on the wall boundaries. The majority of wall rules include constraints in tolerable models Y-plus values.
On the other hand, the ratio of turbulent and laminar flow effects in a cell is represented by Y-plus. If Y-plus is low, the cell’s flow is laminar. If Y-plus is large, the current in that cell will be turbulent. As a result, if Y-plus is too small, then the flow in the cell is prolonged, and the wall functions will not be usable. Therefore, your solver may make incorrect assumptions, mainly when performing the Standard Wall Function computations. Also, if Y-plus is too large, solving the laminar/turbulent flow field in the boundary element is not too difficult, but other assumptions will be incorrect.
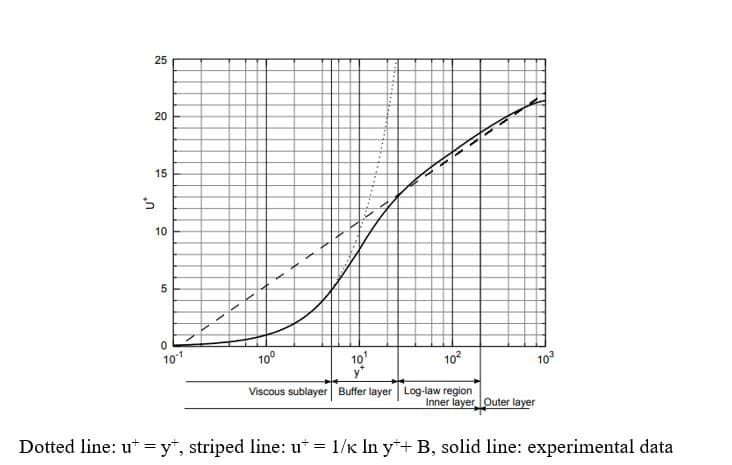
This number usually is about 1 in simulations without wall functions, whereas wall functions allow us to take a y+ greater than 1. The boundary layer can be divided into two regions: the inner and outer layers. The viscous sublayer (y+ <5), the buffer layer (5 <y+ <30-50), and the log-law area (y+ > 30-50) are the three zones that run from the wall to the outer layer in the former.
Wall functions
As previously stated, near-wall flow fields necessitate careful attention. Direct application of the no-slip condition and wall functions that derive the shear stress at the wall using semi-empirical equations are the two basic ways of obtaining the shear stress at a wall in RANS. The dimensionless variable y+ represents the distance from the wall to the first grid cell’s center. The first method’s y+ is usually around 1, but wall functions allow us to use a y+ greater than 1. As a result, there are fewer grid cells and, as a result, faster computing times.
The law of the wall
Viscosity and wall shear stress are important characteristics close to the wall. We define viscous scales, which are the suitable velocity and length scales in the near-wall area, based on these variables (and). The friction velocity is as follows:
The inner layer
In dimensionless form, the law-of-the-wall for this layer is:
From y+ = 30-50 to the outer boundary of the law-of-the-wall region, which is dependent on the Reynolds number, the log layer is valid. We can see this layer’s law-of-the-wall in the dimensionless form as follows:
Where B is a constant and is the von Kármán constant. This is the wall’s logarithmic law. The buffer layer is placed in the 5 <y+<30-50 areas. In this area, neither of the laws apply. The obtained expressions illustrates in the above Figure.
Mesh Quality
The mesh quality considerably impacts the numerical computation’s accuracy and stability. Node point distribution, smoothness, and skewness are linked with mesh quality.
Checking the quality of your mesh, regardless of the type of mesh used in your domain, is critical. Different quality parameters are examined depending on the mesh cell types (tetrahedral, hexahedral, polyhedral, etc.):
- Cell Squish is a metric for determining how far a cell deviates from orthogonality in terms of its faces.
- On Tri/Tet elements, there is a skew in cell equivolume.
- Polyhedral meshes have face squish.
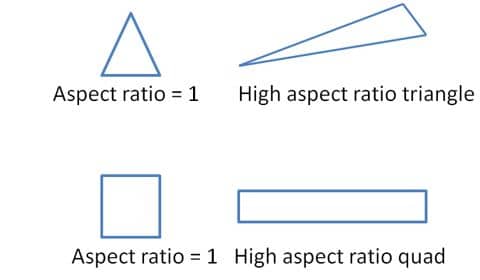
- All meshes have the same aspect ratio.
The aspect ratio is a measurement of a cell’s stretching. We can calculate as the ratio of any of the following distances’ greatest to minimum values: the distances between the cell centroid and the face centroids and the cell centroid and nodes. The figures below depict the aspect ratio of a unit cube as 1.732 because the maximum distance is 0.866 and the minimum distance is 0.5. Using this definition, we can define any mesh, including polyhedral meshes.
Use the Report Quality button on the General task page to check the quality of your mesh:
Clustering and Node Density
Because you’re discretely defining a continuous domain, the density and distribution of nodes in the mesh determine how well the flow’s key features (such as shear layers, separated regions, shock waves, boundary layers, and mixing zones) resolves. Poor resolution in important locations can substantially affect flow characteristics in many circumstances.
The resolution of the boundary layer upstream of the point of separation, for example, is critical in predicting separation due to an adverse pressure gradient. The boundary layer resolution also influences the accuracy of the estimated wall shear stress and heat transfer coefficient accuracy of the estimated wall. It influences shear stress and heat transfer coefficient by the boundary layer resolution (i.e., mesh spacing near walls). This is especially true in laminar flows when the mesh adjacent to the wall must respect the laws of physics.
To obtain good quality in ANSYS Fluent meshing, we must evaluate its smoothness or quality, Skewness, aspect ratio quality, and mesh based on these patterns.
skewness
Smoothing in ANSYS Meshing aims to increase element quality by shifting node locations related to other nodes and elements. It controlles the amount of smoothing iterations and the threshold metric at which the mesher will begin smoothing by the low, medium, or high options.
Smoothness
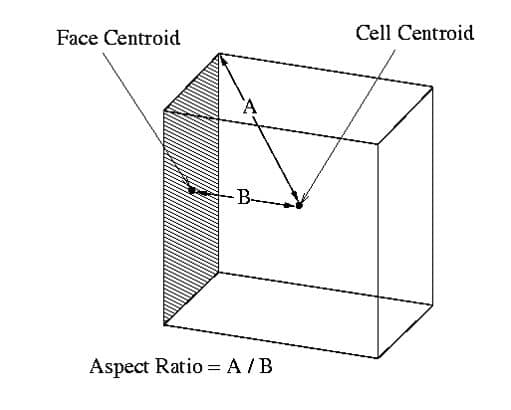
Smoothing in ANSYS Meshing aims to increase element quality by shifting node locations related to other nodes and elements. It controlles the amount of smoothing iterations and the threshold metric at which the mesher will begin smoothing by the low, medium, or high options.
Also, the transition in size should be as smooth as possible. We can avoid sudden changes in cell size because they may cause erroneous results at nearby nodes.
Aspect Ratio
It is the ratio of a cell’s maximum to minimum side. To get the greatest results, it should ideally be equal to 1. It should be close to one for multidimensional flow. Local variations in cell size should also be kept to a minimum, with adjacent cell sizes not differing by more than 20%. A big aspect ratio can cause an interpolation inaccuracy of unacceptable magnitude.
ANSYS Mesh Refinement?
The solution-adaptive mesh refinement function in ANSYS FLUENT lets you refine and coarsen your mesh depending on geometric and numerical solution data. ANSYS FLUENT also includes tools for designing and viewing adaptation fields tailored to specific applications.
You can Select Insert> Refinement from the context menu by right-clicking. Select Refinement from the drop-down list when clicking Mesh Control on the Context Toolbar. Scope the geometry whose mesh you wish to refine in the Details View. Choose a Refinement value between 1 (the smallest refinement) and 3 (the most refined refinement) (maximum refinement).
STUDY OF MESH INDEPENDENCE
You can use the finer the mesh, the more precisely the geometry features capture, and there are more “data points” on the geometry to provide an accurate displacement and stress response.
An analyst can conduct a mesh independence (or grid independence) analysis to determine the results’ reliance on mesh density. One method is to use the strategy outlined below:
- On the geometry, isolate a point of interest. This might be the entire geometry of a small model. However, this is not always possible. Therefore, one might concentrate on a single area of the geometry.
- You can use Obtaining the node count on a radius, chamfer, body, or named selection.
- Refine the mesh in the desired area. There are a few best practices to follow for mesh refinement. The following are some of them:
- Change only the mesh size. We cant change other mesh settings, such as element type or order. This will ensure that the runs are compared fairly.
- Ensure that the increase in mesh count between two runs is “significant.” By significant, we imply a minimum of 10%. This percentage is a guide based on experience and analytical judgment.
- You can see at least three distinct meshes obtain. We can demonstrate Mesh independence with just two meshes. However, mesh independence is often established after three or more passes for rather coarse beginning meshes.
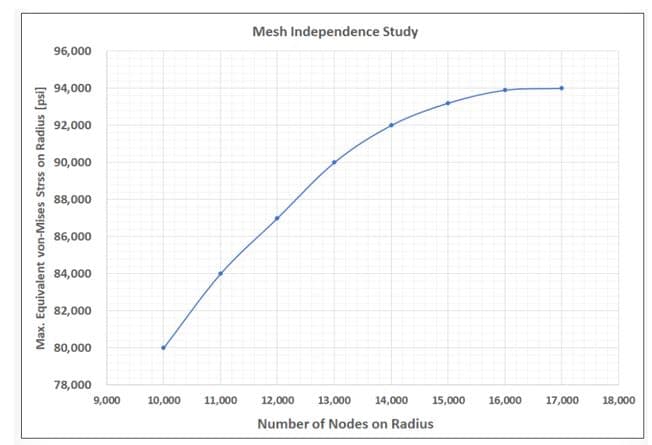
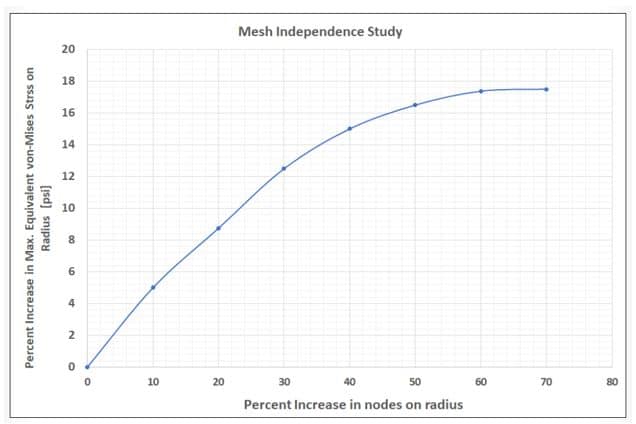
- Compare the outcomes of the different runs. One can look for a point where a big increase in node count does not result in a significant increase in stress by plotting the number of nodes vs. stress. The analyst can plot raw data, percentages, or both.
Mesh independence plots shows in the following Figures. Raw data and percentages both uses to show the same information. We can see that independent mesh stress requires a minimum of 16,000 nodes. This is 94,000-psi stress.

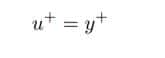
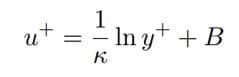




This Post Has 0 Comments