Archimedes Screw Turbine (AST) CFD Simulation
$180.00 Student Discount
- The problem numerically simulates the Archimedes Screw Turbine (AST) using ANSYS Fluent software.
- We design the 3-D model with the Design Modeler software.
- The model is meshed by ANSYS Meshing software, and the element number is more than 2000000 elements.
- The simulation is carried out Transient state and Mesh Motion model.
- The VOF model and Open Channel Flow option are used.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Archimedes Screw Turbine (AST), CFD Simulation, ANSYS Fluent Tutorial
Description
In this project, an Archimedes Screw Turbine (AST) consisting of 3 blades has been simulated. The simulation results have been investigated using ANSYS Fluent software. We perform this CFD project and investigate it by CFD analysis.
Archimedes Screw Generator, also known as Archimedes Screw Turbine (AST), or screw turbine, is a hydraulic machine that uses the principle of the Archimedean screw to convert the potential energy of flow on an upstream level into kinetic energy.
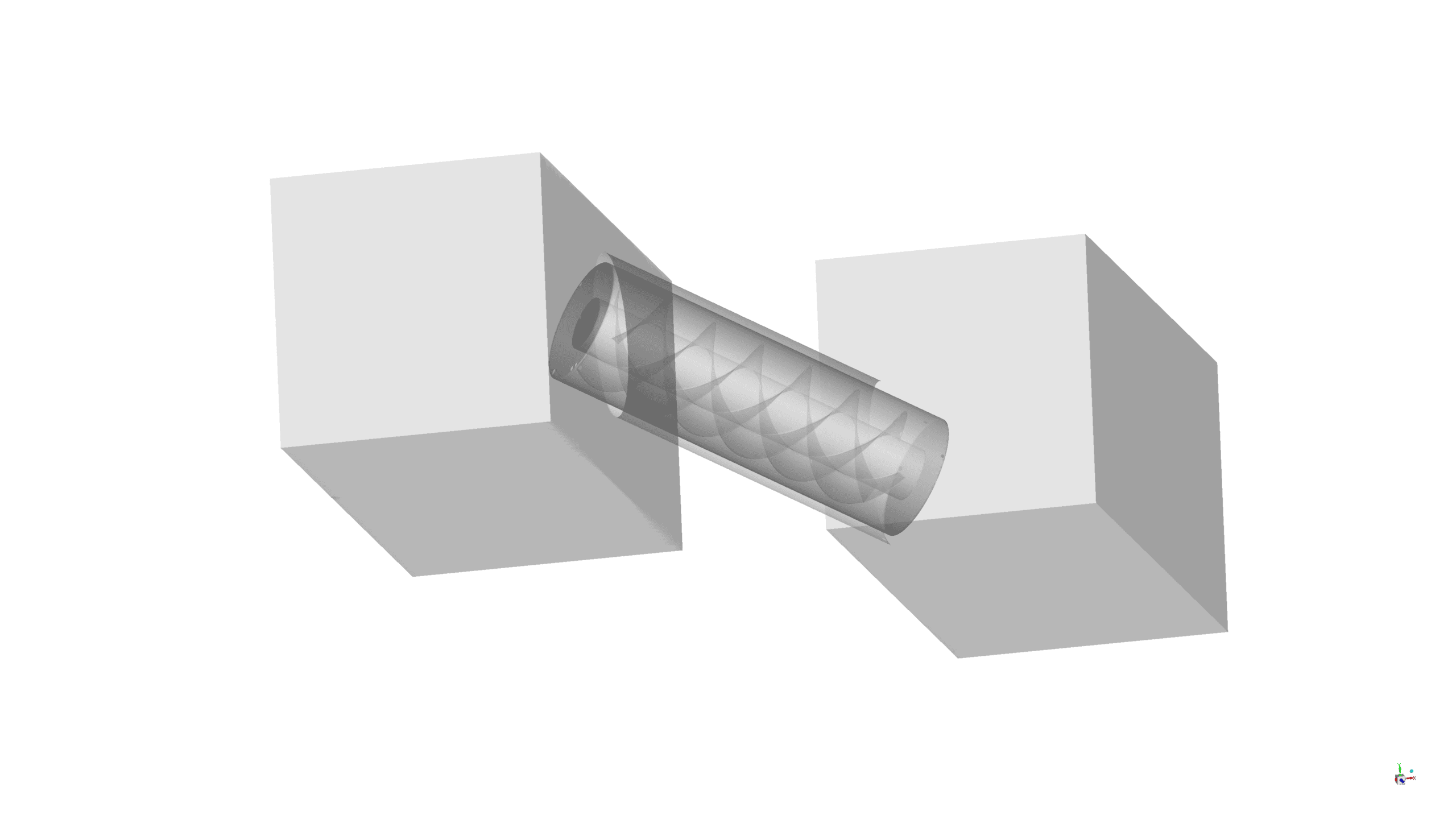
It is assumed that the turbine is set on a river and water fluid flows through it. There is a flow on the upper box of the domain at a fixed level. The turbine has a 30-degree angle with the ground while water enters the domain from the upper level. The gauge pressure in the outlet is zero, and all other faces are stationary walls.
The present model is designed in three dimensions using the Design Modeler software. There are two rectangular boxes at the turbine’s beginning and end, which guide the flow into the turbine, and finally, the water exit from it. The turbine’s interior and exterior radius is 0.5 m and 1 m, respectively.
This geometry has meshed in ANSYS Meshing software, and the number of them is more than 2 million elements.
Archimedes Screw Turbine Methodology
The preferred method for the rotational movement of the turbine is an unsteady Mesh Motion. Considering the conception of this method, (the Mesh Motion method), the rotating zone contains the Screw Turbine that rotates independently.
The VOF model is used to define the water and air phases. Also, the upper level of the domain contains water at a fixed level using the Open Channel Flow option.
The two-equation Standard k-epsilon model simulates the turbulence in the flow.
Archimedes Screw Turbine Conclusion
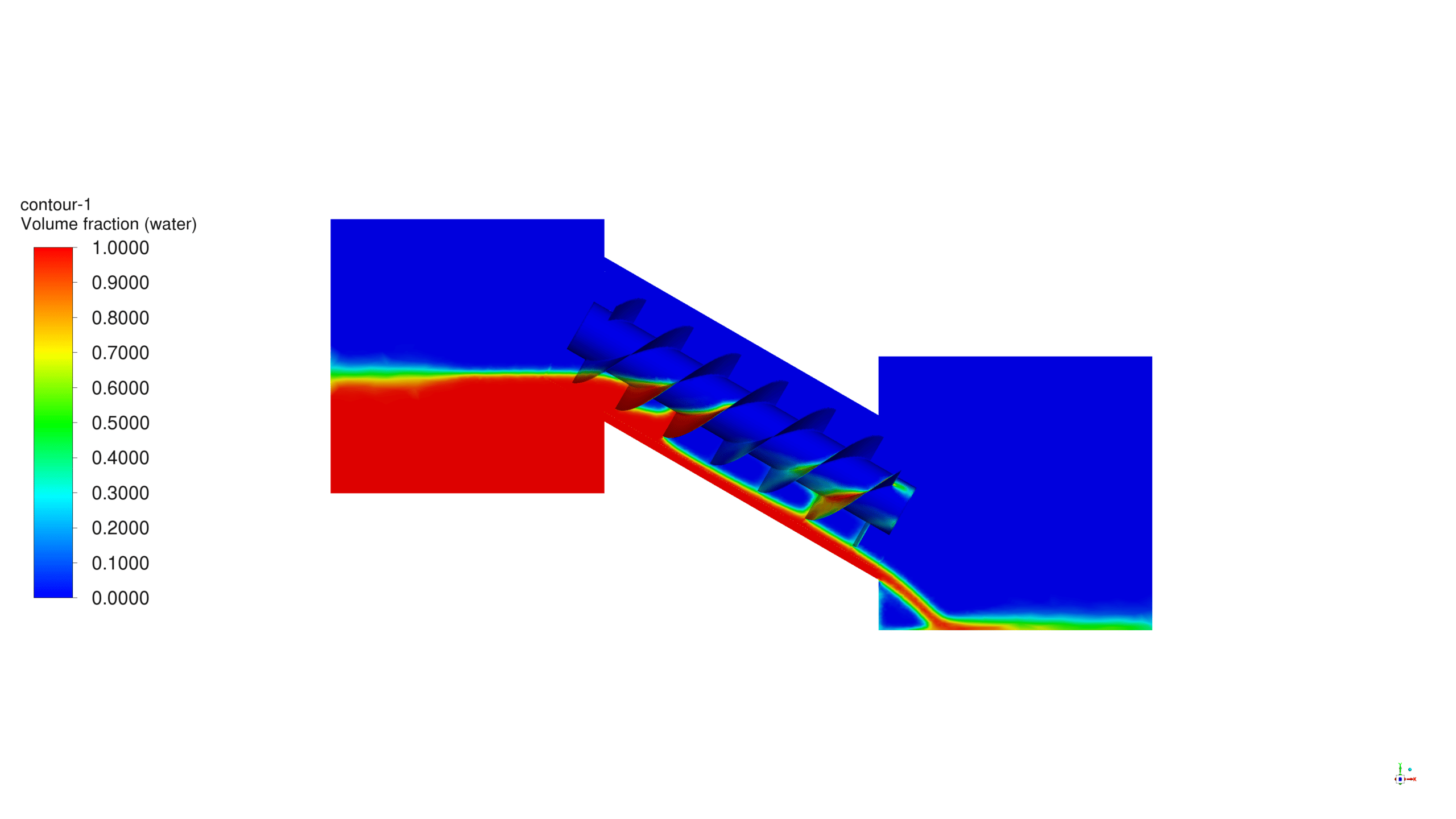
At the end of the solution process, two and three-dimensional contours and vectors related to water pressure and velocity are obtained. At first, water flow enters the upper box, passes over the turbine blades, and moves to the outlet face.
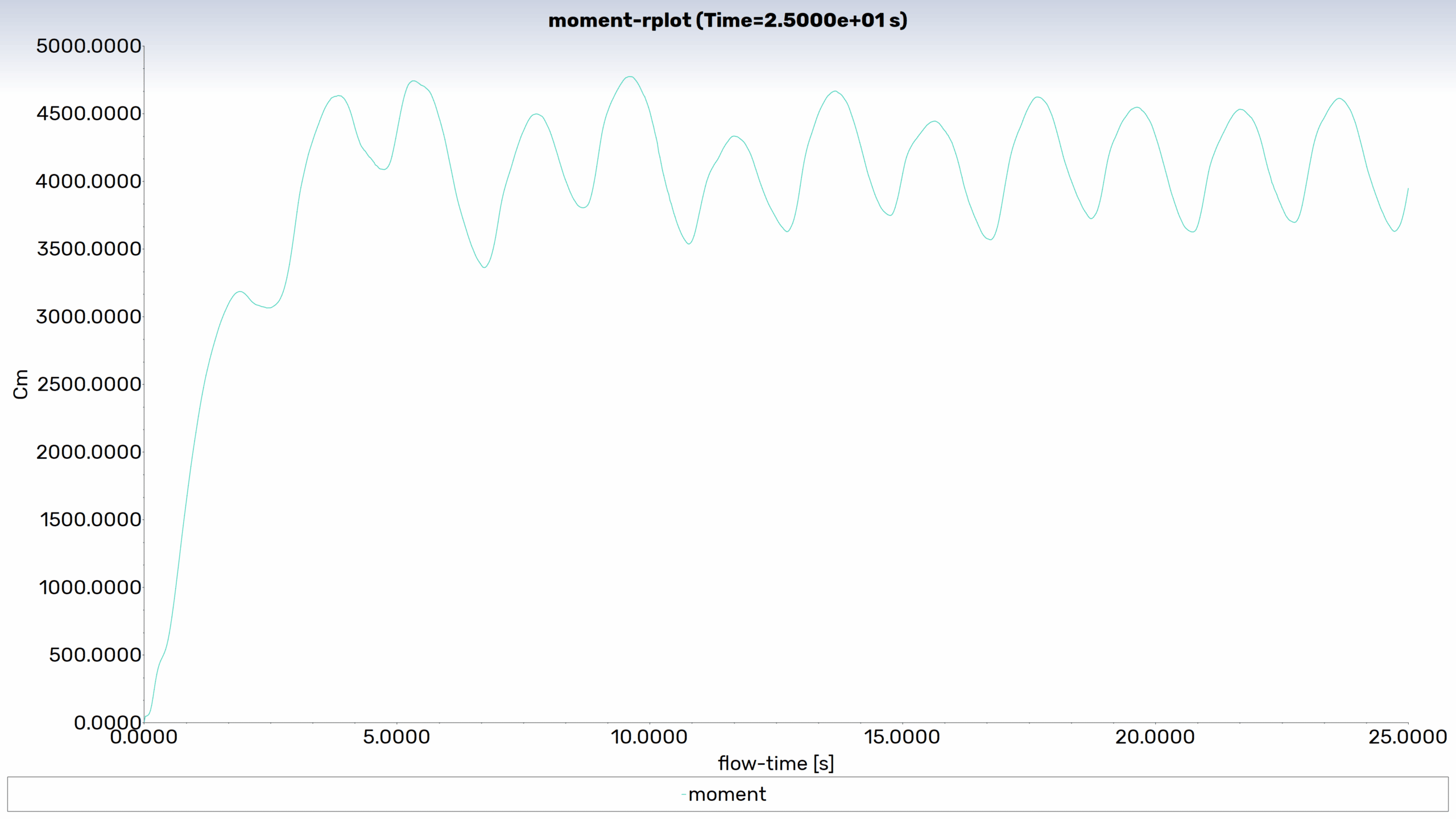
The output power of the turbine is calculated and its maximum amount for the angular velocity of 10 rpm is approximately equal to 5 kW. The Output power is equal to the Moment parameter obtained by ANSYS Fluent multiplied by the angular velocity of the turbine in radians per second which for this project is 1.05. The following figure shows the Moment parameter changes at different times of the solution.
Also, static pressure contour is obtained in the whole domain; as can be seen, it decreases while passing through the channel.
Call On WhatsApp
Bryana Huels –
I found the CFD simulation of the AST fascinating. The flow of water through the blades and the power generation process was modeled with great detail. It was especially helpful to see the moment parameter changes and how the static pressure contour decreases through the channel. Excellent practical learning tool!
MR CFD Support –
We’re thrilled to hear that our comprehensive CFD simulation of the Archimedes Screw Turbine was informative and beneficial to your understanding. It’s wonderful that you could visualize the detailed processes and changes in parameters. Thank you for your positive feedback!
Amya Kertzmann –
Can Archimedes Screw Turbines generate power in a low-flow river, and if so, how effective are they in such conditions?
MR CFD Support –
Yes, Archimedes Screw Turbines can be effective in low-flow conditions. Due to their design and operational characteristics, they can work at lower flow rates and heads, making them scalable for small rivers and streams. Their efficiency in low-flow conditions would depend on the specific design and site characteristics, but they are generally tailored to operate well in such scenarios and can still produce a reasonable output of power.
Tyree Gaylord –
I learned a lot from the AST CFD simulation tutorial. Everything was explained in great detail which really enhanced my understanding. The moment parameter plot was particularly enlightening!
MR CFD Support –
We’re delighted to hear that the tutorial on Archimedes Screw Turbine CFD simulation was so informative and helpful to you! Thank you for appreciating the details provided, especially on the moment parameter plot. It’s great to know our tutorial was able to enhance your understanding effectively. Thank you for your valuable feedback!
Prof. Muhammad Kshlerin IV –
I was truly fascinated by the outcome of the project. It looks like the well-designed simulation provided a thorough analysis of the turbine’s performance.
MR CFD Support –
Thank you for your positive feedback on our Archimedes Screw Turbine CFD Simulation tutorial. We’re delighted to hear that you are impressed with the depth of the analysis and the performance outcome of the simulation. Your satisfaction is paramount to us, and we’re glad we could meet your expectations!
Mariane Grimes Sr. –
I applaud the detailed CFD analysis of the Archimedes Screw Turbine using ANSYS Fluent. This appears to wonderfully combine the dynamics of fluid mechanics with advanced simulation techniques to predict the performance of the AST effectively. Understanding flow properties and calculating the potential power output are crucial aspects of renewable energy equipment design, and this project seems to cover these intricacies well. Obtaining the Moment parameter fluctuations further adds to the clarity and robustness of the simulation results. Brilliant work!
MR CFD Support –
Thank you for your kind words regarding the Archimedes Screw Turbine CFD Simulation project using ANSYS Fluent. We’re thrilled to know that you found the detailed analysis and the combination of fluid dynamics with simulation techniques to be thoroughly effective. It’s great to hear that you recognize the significance of accurate flow property analyses and power output predictions in the design of renewable energy mechanisms. Your appreciation for the data regarding the Moment parameter’s variation over time is particularly pleasing, reaffirming the comprehensiveness of our simulation study. Your enthusiastic feedback motivates us to keep providing high-quality, valuable learning products.
Mr. Kelley Roob –
I’ve never seen a simulation for Archimedes Screw Turbines before. The results you describe are fascinating; how efficient is this type of turbine compared to traditional hydroelectric generators?
MR CFD Support –
The Archimedes Screw Turbine (AST) tends to have high efficiency across a range of flow rates, which is favorable in locations where water flow varies. However, its efficiency might be slightly lower compared to highly optimized conventional hydroelectric generators, especially at large scales. Its efficiency also depends on the design specifics and operating conditions of the system.