ACSC Performance with Diffuser Orifice Plate, Validation
$360.00 Student Discount
- The problem numerically simulates ACSC Performance with Diffuser Orifice Plate using ANSYS Fluent software.
- We design the 3-D model with the Design Modeler software.
- We Mesh the model by ANSYS Meshing software, and the element number equals 2668772.
- This project is simulated and validated with a reference article.
- We use the Fan boundary condition and define a Pressure Jump.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
ACSC Performance with Diffuser Orifice Plate, Paper Numerical Validation, ANSYS Fluent CFD Simulation Tutorial
This project simulates the ACSC system in a 600 MW power plant based on the article “Effects of a diffuser orifice plate on the performance of air-cooled steam condenser.” The results of the current numerical CFD simulation work are compared and validated with the reference paper by ANSYS Fluent software.
The main purpose of designing and using these systems in power plants is to prevent energy waste; In this way, these systems condense the hot steam from the turbine and transfer the water from the distillation process to the pump section of the steam turbine.
The power plant studied in the present work consists of 7 rows of ACSC systems. The fourth row is studied in this CFD simulation. Each row of ACSC systems consists of eight fans, and each of these fans is located under two diagonally porous plates.
The operation of these systems is such that the hot and low-pressure steam of the turbine outlet passes through each of the pipes and then is transferred to the interior space of the diagonal plates installed on both sides of that pipe.
The present 3-D model is designed using SOLIDWORKS and Design Modeler software. The geometry is related to a cooling system consisting of eight rows of hot steam pipes, diagonally porous plates on either side of each pipe, and eight fans on one platform.
The meshing of the present model is done using ANSYS Meshing. The mesh type of the model is hybrid, and the element number is 2668772.
ACSC Methodology
The purpose of the problem is the distillation process; Therefore, a constant saturation temperature for steam must be defined; Because the condensation process takes place at saturation temperature at a constant pressure. This value is 319.75 K.
Also, the fan boundary condition is considered for each of the eight installed fans. In the Fan boundary condition, a pressure jump must be used; Because there will be a pressure difference on both sides of the fan in the specified direction.
The amount of pressure jump is obtained based on a polynomial function in terms of the axial velocity passing through the fan surface; Hence, a polynomial is imported in this section.
ACSC Conclusion
After simulation, the 3D contours related to the velocity, pressure, and temperature are obtained. The temperature contour shows that the open air transfers its heat to the steam pipe for condensation to occur.
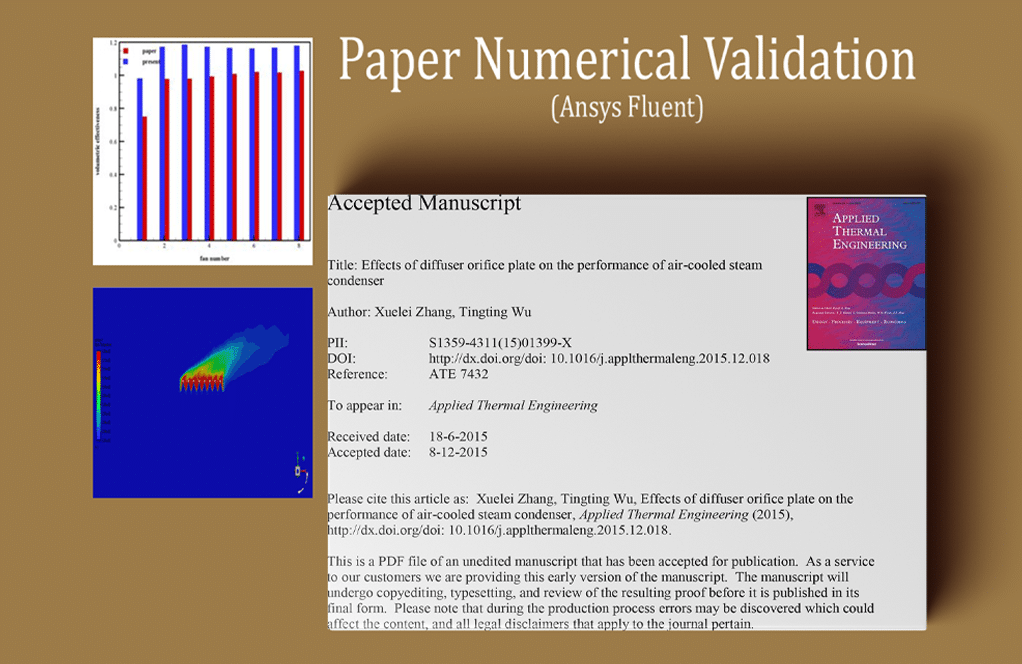
Also, The graph of volumetric effectiveness changes in terms of the fan number in the system is obtained and validated with the results of the source paper.
The diagram under consideration in the article is related to Figure 5-c. The main purpose of this work is to investigate the effect of open airflow velocity on the performance of the fans of the system in terms of volume transfer from the cooling airflow.
Then, a dimensionless parameter is defined to investigate the volumetric flow rate of the fans. This parameter is equivalent to the ratio of the volumetric flow rate transferred from the fans resulting from the numerical solution to the volumetric flow rate flowing from the fans in the ideal state.
The ideal volume flow rate is 428 m.s-1, and the dimensionless parameter is called volumetric effectiveness. A comparison between the results of the present work and the results of the article confirms that the accuracy of the solution is acceptable, and the error is low.



Amely Zieme –
How do we know the project is done right?
MR CFD Support –
This project simulates the ACSC system in a 600 MW power plant based on the article “Effects of a diffuser orifice plate on the performance of air-cooled steam condenser,” and the results of the current numerical CFD simulation work are compared and validated with the reference paper by ANSYS Fluent software.
Marielle Thompson –
This simulation is a testament to the power of computational fluid dynamics!
Miss Meagan Feil I –
What is the benefit of using CFD for analyzing the effects of a diffuser orifice plate on ACSC performance?
MR CFD Support –
CFD allows for detailed analysis of the flow patterns and heat transfer processes in an ACSC, providing insights that cannot be easily obtained through experimental tests.
Sandra Muller –
It had some useful and interesting points, thanks
Brianne Mills –
This simulation is a fantastic tool for understanding the complex flow phenomena in an ACSC!
Amari Senger –
The CFD simulation results clearly demonstrated the impact of the diffuser orifice plate on the ACSC system’s performance. The contours provided a deep insight into the temperature variations indicating effective heat transfer. As a customer, I am really intrigued by how well the actual performance was captured and the validation against the published data instilled additional confidence in this analysis.
MR CFD Support –
Thank you for your positive feedback! We’re delighted to hear that our simulation results and the detailed validation against empirical data have met your expectations and provided you with valuable insights into the performance of the ACSC system. Our aim is to ensure the accuracy and reliability of our CFD simulations, and it’s gratifying to know that our efforts have resonated well with you. Should you have any more questions or need further clarifications on our products, don’t hesitate to reach out!
Robin Strosin –
The tutorial material you have provided was so comprehensive and made the whole learning process about ACSC performance quite enriching. Seeing the 3D contours and understanding the temperature dynamics have given me a solid grasp on the effectiveness of cooling systems in real-world applications.
MR CFD Support –
Thank you so much for your positive feedback! We’re thrilled to hear that the tutorial on ACSC performance with a diffuser orifice plate was helpful and informative for you. It’s great to know that the 3D contours and temperature dynamics illustrated in the simulation gave you useful insights into cooling systems. If there’s anything else we can help you with, please let us know.
Harrison Pacocha –
I appreciate the commitment to accuracy and validation in this simulation.
Gardner Goodwin –
I’m thrilled with the results from the ACSC Performance with Diffuser Orifice Plate tutorial – especially how the volume effectiveness matches with the reference paper. Great work on ensuring the validity of the simulation results!
MR CFD Support –
Thank you for your kind words! We’re delighted to hear that you found our tutorial on ACSC Performance with Diffuser Orifice Plate useful and accurate. We always strive to provide high-quality, validated simulations to ensure helpful learning experiences. Your feedback is appreciated!
Zora Heller –
I just completed the ‘ACSC Performance with Diffuser Orifice Plate’ CFD Simulation tutorial. The step-by-step guidance was incredible and made the complex process straightforward to understand. The validation process based on the article was quite in-depth, and it gave me a lot of confidence in the simulation results. The use of polynomial functions for the Fan boundary condition was particularly insightful!
MR CFD Support –
Thank you for your kind words! We’re thrilled to hear that our tutorial was helpful and that you appreciate the detailed validation process. Our goal is always to provide clear and thorough guidance to ensure our users feel confident in their simulation results. If you have any further questions or need additional support, never hesitate to reach out. Thank you for choosing our tutorial!
Mrs. Elena Wisozk II –
The ACSC simulation tutorial was spot on! It was very straightforward to follow, and all the steps were clear. The validation with the reference paper really provided confidence in the simulation results. Fantastic job!
MR CFD Support –
Thank you for your wonderful feedback! We are thrilled to hear that our ACSC simulation tutorial was helpful and easy to follow. It’s great to know that the validation aspect added to your confidence in the results. We appreciate you taking the time to compliment our product. If there’s anything more we can do to assist you, please let us know!
Sandrine Vandervort –
I was thoroughly engaged by the tutorial for simulating the ACSC system. The validation with the academic paper gave me a lot of confidence in the accuracy of the CFD analysis. The step-by-step approach really helped in understanding the complex interaction of airflow and temperature regulation. Truly, a well-executed tutorial!
MR CFD Support –
We greatly appreciate your positive feedback on the ACSC system simulation tutorial. It’s wonderful to know the validation aspect and our step-by-step approach contributed to your understanding and confidence in the analysis. We strive to provide comprehensive learning materials, and it’s rewarding to hear that our efforts are making a difference. Thank you for your kind words and for choosing our tutorials!
Miss Jannie Grady –
This CFD simulation tutorial sounds robust and very thorough in detailing the ACSC system’s performance. I found the incorporation of distillation process conditions and the polynomial defining the fan boundary condition particularly impressive. Excellent work in matching up with the paper’s results — an essential aspect of validation studies.
MR CFD Support –
Thank you for recognizing the detail and robustness of the CFD simulation tutorial on the ACSC system’s performance. Your appreciation motivates our team to continue delivering high-quality validation studies that can be essential resources for professionals and enthusiasts in the field. We’re delighted to hear that our efforts in comparing and validating results have met your expectations. Should you need any further information or assistance, feel free to get in touch!
Shawna Hill IV –
I’m interested to know if the comparison with the reference article findings included local performance indicators or only overall system behavior metrics?
MR CFD Support –
The comparison focused on overall system performance metrics, particularly the volumetric effectiveness parameter. It’s a dimensionless number representing the ratio of actual to ideal volumetric flow rates of the fans based on the numerical simulation versus actual plant operation data.
Dr. Edyth Grimes –
The project simulations from MR CFD Company on ACSC Performance with Diffuser Orifice Plate was a great learning experience. The tutorial provided all the necessary setups and results comparisons to aid in my understanding of the system.
MR CFD Support –
We’re delighted to hear that you found the ACSC Performance with Diffuser Orifice Plate tutorial informative and helpful for your understanding. At MR CFD, we aspire to provide clear and thorough guidance on various CFD simulations. Thank you for choosing our tutorial and we appreciate your positive feedback!
Lon Mertz –
This tutorial seems very comprehensive. Could you please clarify if the airflow over the ACSC system is simulated as turbulent, and how is the turbulence modeled?
MR CFD Support –
In this simulation, airflow over the ACSC (Air-Cooled Steam Condenser) system is indeed simulated as turbulent. The turbulence is typically modeled using one of the turbulence models available in ANSYS Fluent, such as the standard k-epsilon, RNG k-epsilon, Realizable k-epsilon, SST k-omega, or another appropriate model depending on the specifics of the case and fidelity required. The model choice is informed by the need to accurately capture the turbulent flow characteristics and heat transfer phenomena in the steam condenser system.
Nigel Ledner –
I’m impressed with the detailed validation process outlined for the ACSC simulation. It sounds very intricate yet effective in ensuring accurate simulations!
MR CFD Support –
Thank you for your positive feedback on the ACSC Performance with Diffuser Orifice Plate CFD simulation tutorial! We are glad to hear that you find the validation process detailed and effective. Ensuring accuracy in our simulations is highly important for us, and it’s rewarding to see that it is recognized by our customers. If you have any more questions or need further assistance, please don’t hesitate to reach out.
Malika Veum –
The tutorial did a great job verifying against the reference paper. Were all aspects of performance measured, or were there any additional data or metrics that the tutorial didn’t cover?
MR CFD Support –
Thank you for your kind words. The tutorial primarily focused on verifying the simulation against the reference paper’s findings, including the volumetric effectiveness which evaluates the performance of the fans. All major performance aspects, in terms of airflow, pressure, and temperature distributions, were covered to validate the model adequately. While the primary metrics were accounted for, any additional data not included in the publication was not part of this tutorial’s scope.
Mr. Buck Schaden Jr. –
The ACSC performance simulation was impressive. I was particularly amazed by the excellent detail in implementing the fan boundary conditions and the clear presentation of effectiveness shown through the validation process. The results were robust and effectively mirrored the source material, reflecting the precision of your simulation work.
MR CFD Support –
We appreciate your positive feedback! It is encouraging to hear that the attention to detail and effort to validate our simulation against the source material met your expectations. Should you have any further inquiries or need more information about this or other simulations we offer, please feel free to reach out to us.
Billie Hauck –
I’m particularly impressed by the level of detail presented in the contours of velocity, pressure, and temperature. Seeing the transfer of heat between the air and steam pipe visually clarified the condensation process for me.
MR CFD Support –
Thank you for your positive feedback. We are thrilled to hear that our simulation’s detailed results provided a clear understanding of the condensation process. If you have any other insights or need further clarifications, feel free to reach out to us!
Dr. Akeem D’Amore Sr. –
The tutorial and validation results provided a great understanding of the ACSC system simulation, and it was really helpful to see the comparative analysis with the real-world data. It’s impressive to see such an in-depth simulation successfully mirror the actual system performance within a low margin of error.
MR CFD Support –
Thank you so much for your positive feedback! We’re delighted to hear that you found the validation and the tutorial useful and that the comparative analysis met your expectations. Accurate modeling and validation against real-world scenarios is at the core of our approach. If you need further assistance or information on our products, please don’t hesitate to reach out.
Ms. Felicita Kreiger –
I am extremely impressed with the validation of the ACSC performance simulation against the source paper’s data! The attention to detail in establishing the pressure, temperature, and velocity conditions necessary for accurate results is commendable. It’s great to see the use of a hybrid mesh to increase simulation accuracy.
MR CFD Support –
Thank you for recognizing the effort we put into validating the ACSC system’s performance. At MR CFD, we strive to ensure our simulations are not only accurate but also useful for practical applications. The use of hybrid mesh indeed plays a crucial role in delivering high-quality results. We appreciate your feedback and are delighted to hear that the tutorial met your expectations!
Alfonzo Grady –
I’m impressed with the accuracy of the simulation results when compared to the research paper. The comprehensive explanation in the product description clearly outlines the methodology and objectives. Great work!
MR CFD Support –
Thank you for your kind words and recognizing the precision of the simulation work. We strive to provide detailed and accurate simulations for instructional purposes. We’re glad to hear that our efforts have met your expectations!
Dave Turcotte –
This product seems very comprehensive. Great work on the accuracy and detailed comparison with the reference paper!
MR CFD Support –
Thank you for your kind words! We strive to provide accurate and detailed analyses in our simulations to ensure they are as useful as possible. We’re glad to hear that you found the comparison with the reference paper helpful.