Non-Equilibrium Porous Aluminum Foam Heat Sink, Paper Validation
$240.00 Student Discount
- The problem numerically simulates Non-Equilibrium Porous Aluminum Foam Heat Sink using ANSYS Fluent software.
- We design the 3-D model with the Design Modeler software.
- We Mesh the model with ANSYS Meshing software.
- The mesh type is Structured, and the element number equals 87000.
- This project is simulated and validated with a reference article.
- We use a Porous medium made of aluminum foam.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Non-Equilibrium Porous Aluminum Foam Heat Sink, Paper Numerical Validation, CFD Simulation by ANSYS Fluent
This project simulates the inlet airflow to a vertical cylindrical chamber with an aluminum fin connected to a heat source (heat sink). The domain is made of porous material. Non-Equilibrium Porous Aluminum Foam Heat Sink is modeled by ANSYS Fluent.
The results of this simulation are compared and validated with the article “Heat transfer characteristics of aluminum-foam heat sinks with a solid aluminum core.” We design the geometry of the present model using Design Modeler software.
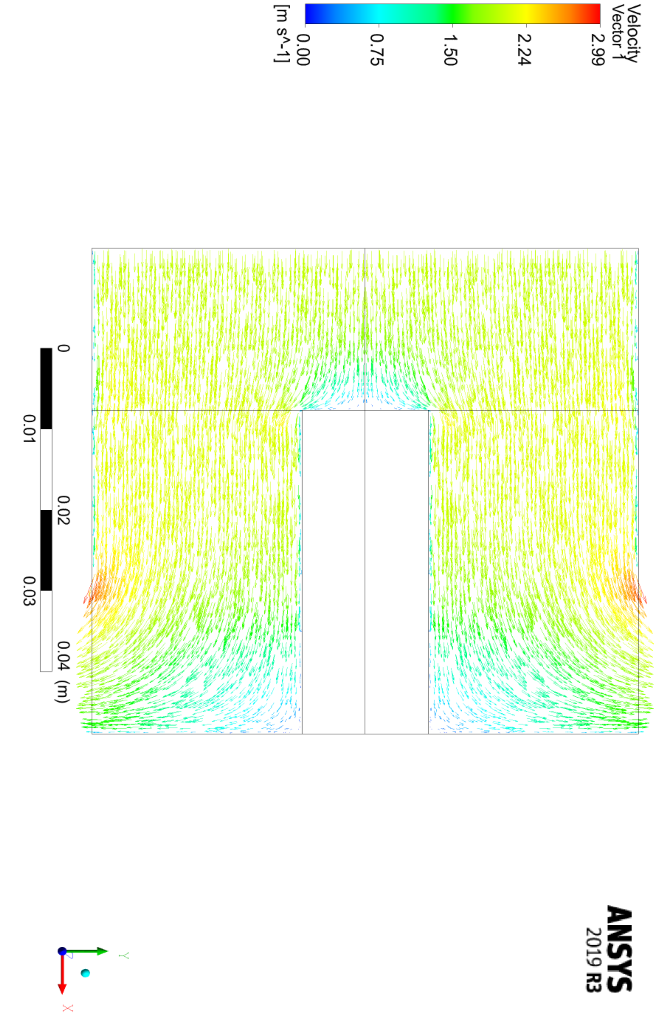
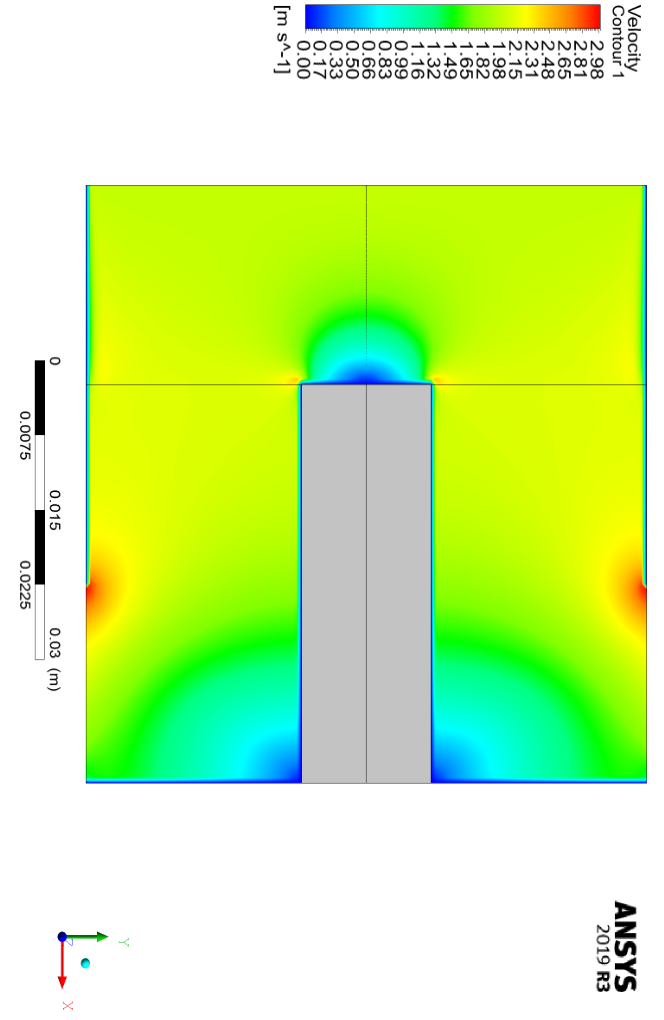
The present model is two-dimensional, and we model it axisymmetric due to its symmetrical structure. This model consists of three main parts: the space for the incoming open airflow, the space related to the porous aluminum zone, and the space for a solid aluminum fin.
We carry out the meshing of the model using ANSYS Meshing software. The mesh type is Structured, and the element number equals 87000.
Methodology
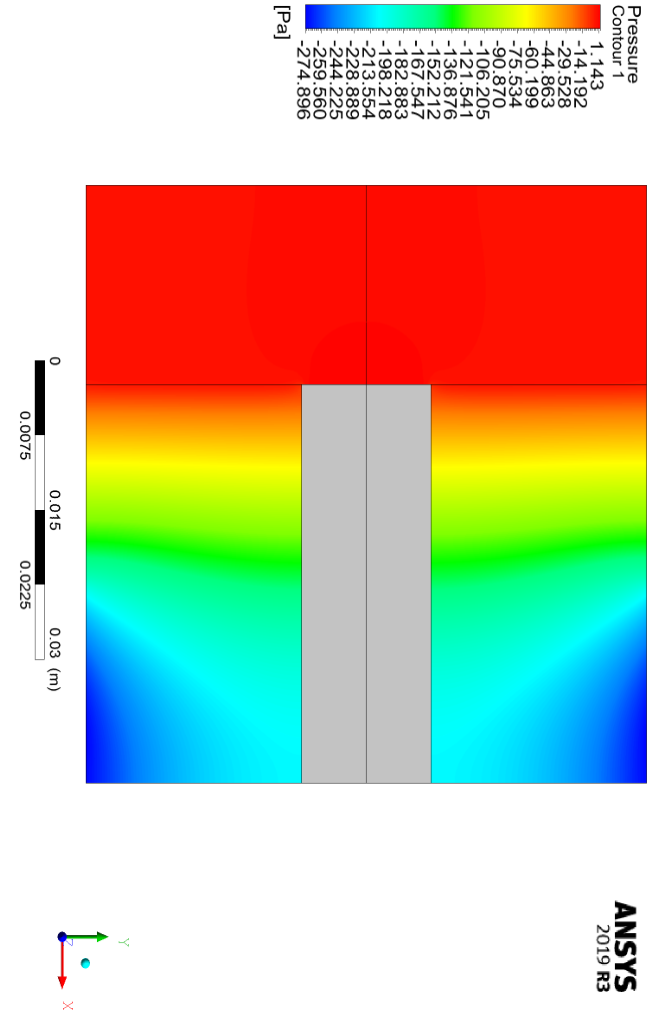
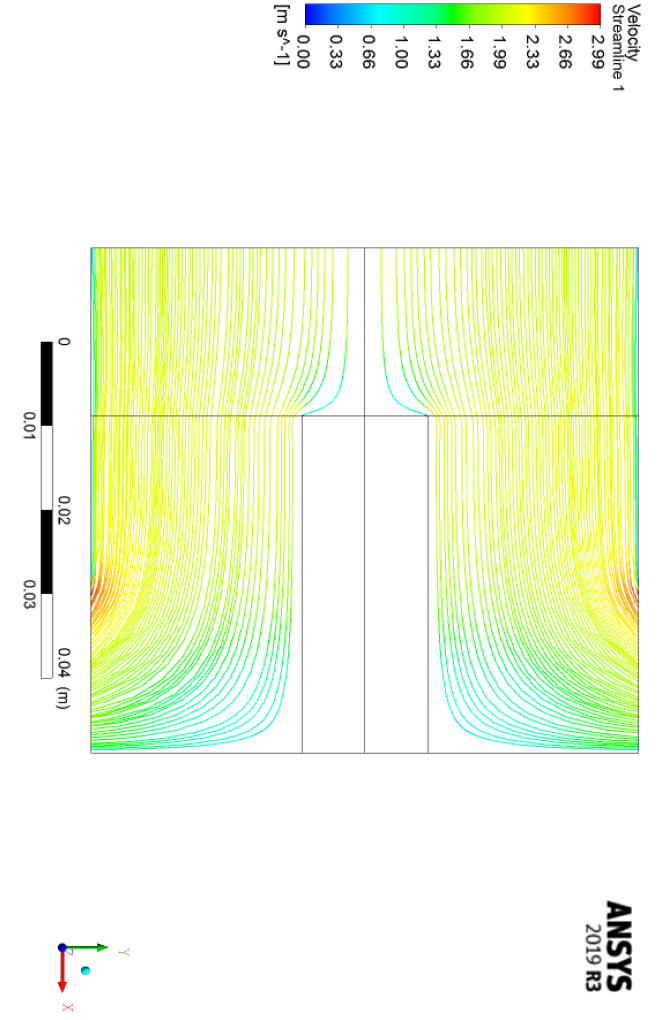
The airflow enters the chamber vertically and downwards from the upper section and exits horizontally from the side sections at the bottom of the chamber. Inlet airflow is assumed to be a developed flow; Hence, the height of the cylinder is assumed to be relatively high.
The inlet airflow has a temperature of 300 K and has variable velocities since the Reynolds number of the model will be variable.
The Reynolds studied in the present numerical work varies between 29 and 89, and therefore it can be said that the model has a laminar flow. At the bottom of the cylinder is a small cylindrical fin that acts as a solid body of aluminum.
A porous environment made of aluminum foam is located in the space between the two outer and inner cylinders. The viscous resistance in a porous medium is the inverse of the fluid permeability in the porous medium, which is equal to 58888270 1/m2 according to the formula in the paper.
According to the article’s formula, the inertial resistance value is 1000.794 1/m. The porosity coefficient in a porous medium is equal to the ratio of fluid space to the total environment space, which in the present problem is equal to 0.87.
The porous zone of the problem is not an equilibrium in terms of temperature; Therefore, the non-Equilibrium option must be enabled. When using non-Equilibrium thermal equations, a term related to the heat source is obtained, which according to the relation Hsf.Asf (Ts-Tf), it is necessary to define the values of Hsf and Asf.
Therefore, according to the article’s formulas, the interface zone density value is assumed to be 2864.27 1.m-1, and the value of the heat transfer coefficient is assumed to be 54.78671 W/m2.K.
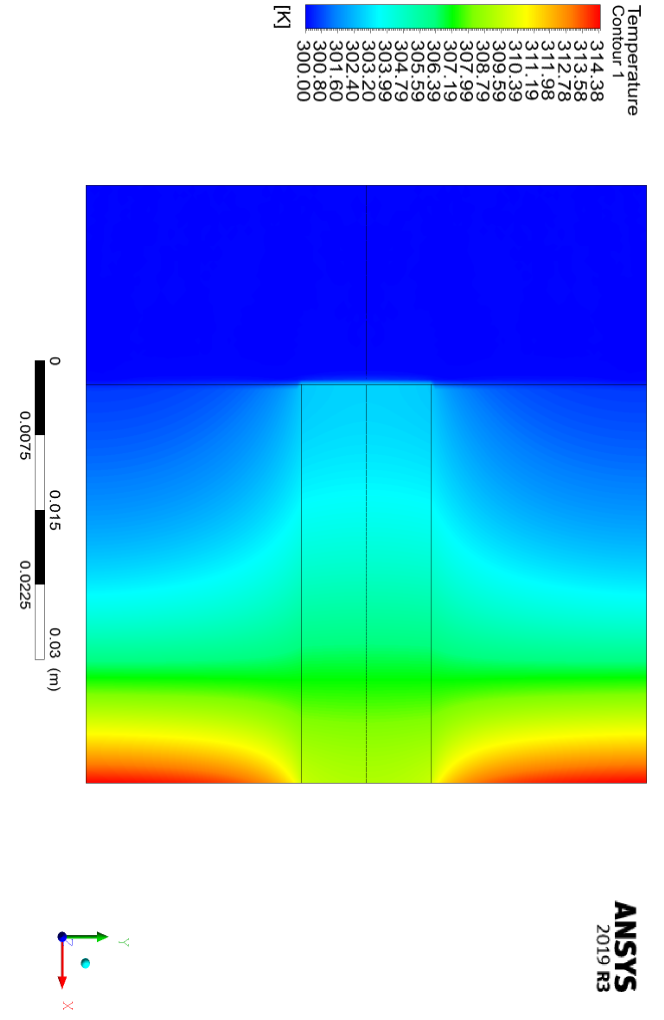
At the bottom of the chamber, a copper heat source is used, which creates a temperature in the range of 320 K to 360 K at the surface of the copper heat source. In this numerical work, it is assumed that the surface of this heat source has a constant temperature of 330 K.
This problem is characterized by the use of interface surfaces in three areas. The boundary between the porous medium and the aluminum fin, the boundary between the air and the aluminum fin, and the boundary between the porous medium and the open air.
In the first two cases, since we use an aluminum solid on one side of the boundary, only heat transfers from the boundary, and there is no mass transfer; In the third case, in addition to heat transfer, mass transfer also occurs.
Conclusion
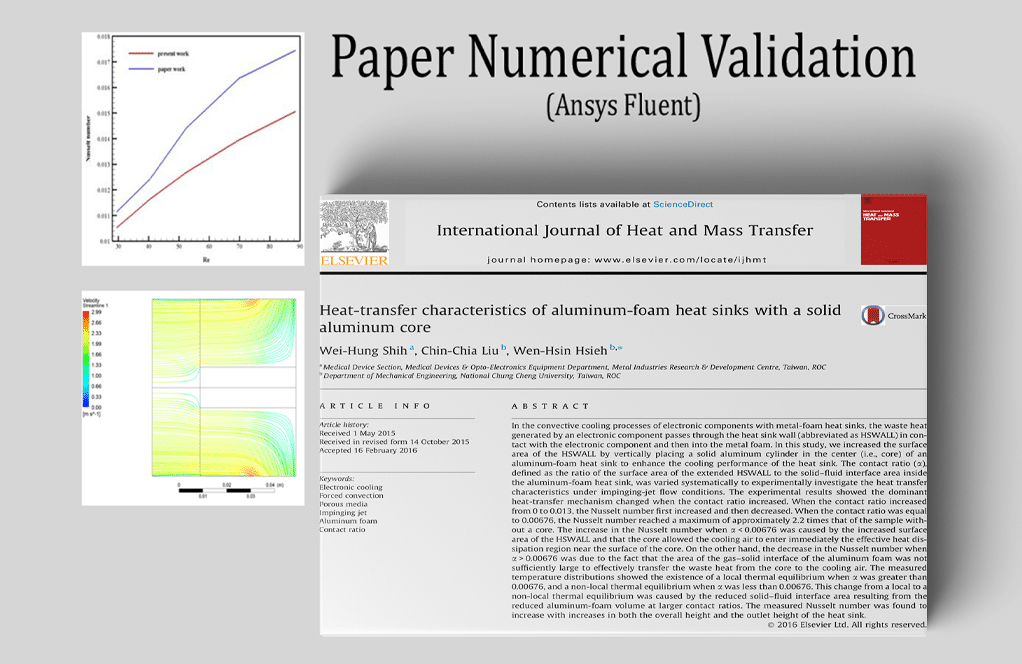
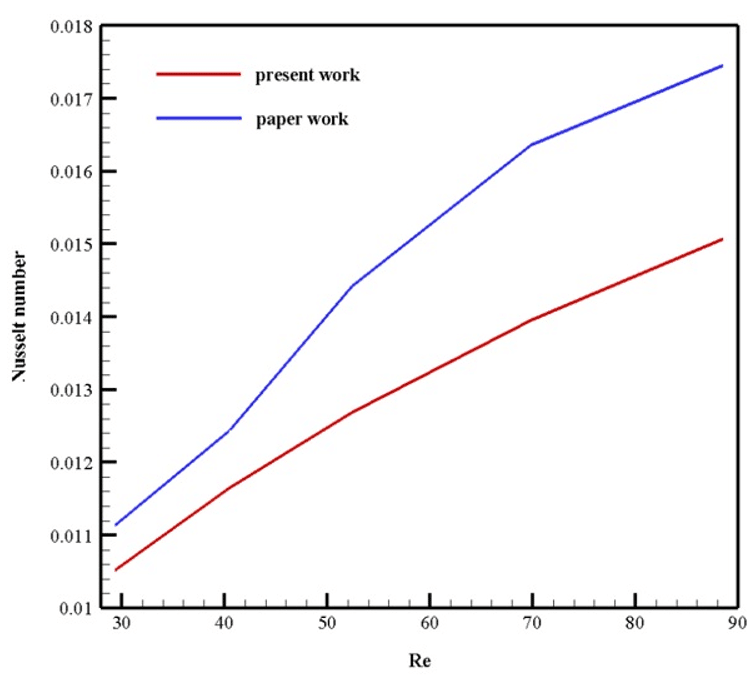
This problem aims to investigate the value of the Nusselt number (equivalent to the convection-conductivity ratio) in the porous region of the chamber in different Reynolds numbers.
At the end of the solution process, we obtain the value of the Nusselt number at the contact surface between the solid fin and the porous material at the bottom of the chamber in terms of different values of the Reynolds number for the incoming airflow.
We validate and compare the results with Figure 3 of the article.



Antonina Leannon –
I really enjoyed seeing how you validated the numerical results with the scientific article. Can you provide me with more details regarding how accurately the model predictions match the article’s data?
MR CFD Support –
Thank you for your positive feedback! We strive to ensure our simulations are accurately validated against empirical data. In this particular simulation, the numerical predictions closely matched the data presented in the article, especially in terms of the Nusselt number across varying Reynolds numbers. The comparison against Figure 3 of the article demonstrated the reliability of our CFD model on capturing the nuanced heat transfer characteristics of the porous aluminum foam heat sink.
Leonel Romaguera –
What specific methods are used in ANSYS Fluent to model the heat transfer in the porous aluminum foam?
MR CFD Support –
In ANSYS Fluent, the heat transfer in the porous aluminum foam is modeled using the Non-Equilibrium thermal model. This involves setting viscous and inertial resistance values for the porous medium, along with a porosity coefficient. Moreover, the non-equilibrium conditions require the definition of the interface zone density, Hsf, and the heat transfer coefficient, Asf, values.
Katheryn VonRueden IV –
The review captures the essence of the product wonderfully, highlighting key elements such as the comparison with the literature, precise use of ANSYS Fluent in simulating intricate flow and heat transfer phenomena, and the clear presentation of methodology and conclusions.
MR CFD Support –
Thank you for the positive feedback! We are thrilled that you found the simulation detail and validation aspects of the product informative and satisfactory. It’s great to know our commitment to accuracy and practical application align with your expectations. If you have further projects or simulations in mind, we’re always here to assist!
Mrs. Calista Baumbach Sr. –
The project description mentioned the use of interface surfaces. Could you explain more about how the interaction at these interfaces affects the simulation results?
MR CFD Support –
At the interfaces, there is a careful consideration of heat and mass transfer between different materials and phases. In the porous medium, the thermal non-equilibrium is crucial to accurately model. This attention to detail ensures that the transfer of heat is well represented, directly affecting the temperature distribution and efficiency of the heat sink. Mass transfer also occurs at the porous-open air interface which can impact the airflow and effectiveness of the heat sink.
Mr. Pedro O’Kon –
I’m really impressed with the depth of analysis, but can you confirm if transient effects are considered in this simulation or is it a steady-state analysis?
MR CFD Support –
Thank you for your kind words. To address your question, the analysis of the Non-Equilibrium Porous Aluminum Foam Heat Sink is a steady-state simulation. It focuses on studying how the Nusselt number relates to Reynolds numbers within a range that ensures laminar flow. There are no transient effects considered in this simulation as the study is designed to validate findings with steady-state conditions as described in the reference article.
Cecile Schowalter –
I really appreciated the detailed explanation of the mesh type and element number. However, could you clarify for me the effect of the interface zone density on the system?
MR CFD Support –
The interface zone density value plays a significant role in the simulation as it represents the physical architecture of the porous medium which, directly impacts the heat transfer coefficient. This, in turn, affects how effectively the heat from the heat source is distributed and transferred across the porous medium, influencing the overall cooling performance of the heat sink.
Johathan Veum –
Just finished going through the CFD simulation course using the Non-Equilibrium Porous Aluminum Foam Heat Sink project. The step-by-step break down made it impossible to get lost, and I feel confident in my understanding. Fantastic learning resource!
MR CFD Support –
Thank you for your kind words about our Non-Equilibrium Porous Aluminum Foam Heat Sink CFD simulation course. We’re thrilled to hear that you found the course content easy to follow and that it has boosted your confidence. It’s our pleasure to provide quality learning resources that help our customers succeed. If you have any further feedback or require more guidance, we’re always here to help!
Elise Will –
I just want to give a big thumbs up for the detailed approach MR CFD Company has taken in this paper validation project. The methodology outlined how each aspect of the simulation addresses the specific nuances of non-equilibrium heat transfer in porous aluminum foam, providing a solid comparison to the research article. Huge kudos for the effort and clear presentation!
MR CFD Support –
Thank you for your kind words! We appreciate your feedback and are delighted that our approach to the Non-Equilibrium Porous Aluminum Foam Heat Sink simulation met your expectations. It’s always our goal to provide detailed and clear presentations. Your acknowledgement truly means a lot to us.
Marcella Rosenbaum –
I’ve noticed the simulation models non-equilibrium conditions in the porous zone. Can the simulation also handle coupled heat transfer within the solid and fluid regions?
MR CFD Support –
Yes, the simulation includes capabilities to handle coupled heat transfer processes within the solid aluminum and the fluid regions by appropriately defining the interface boundary conditions.
Baylee Halvorson –
The product is brilliantly comprehensive and detailed. The validation against existing literature adds immense value, enhancing trust in CFD results and methodology. Kudos to the MR CFD team for exceptional work!
MR CFD Support –
Thank you for your kind words! We’re thrilled to hear that the validation aspect of the product has made such a positive impact on your trust in our CFD methodology. Your satisfaction is our top priority, and we look forward to continuing to provide you with high-quality learning materials.
Lupe Jacobs DVM –
This Advances Numerical Heat Transfer article’s precise methodology for the heat sink simulation is impressive—significant attention to detail in parameter settings for an accurate result. MR CFD courses truly help in understanding complex validations like this.
MR CFD Support –
Thank you for your positive feedback. We’re delighted to hear that our course on Numerical Heat Transfer has enhanced your understanding of complex validation processes in CFD simulations. We strive to provide detailed and accurate learning materials to help our customers succeed.
Jerry Rice –
What happens if you change the temperature of the copper heat source? Will it affect the Nusselt number significantly?
MR CFD Support –
Yes, altering the temperature of the copper heat source would impact the heat transfer characteristics of the system, resulting in a different Nusselt number. This parameter is a key indicator of convective heat transfer, so changes in source temperature can change the heat transfer rate, influencing the Nusselt number outcome in the simulation.
Jalon Walter –
The porous aluminum foam heat sink project sounds intricate and valuable for thermal management. Great detail in the methodology and conclusions. Great job on achieving the validation and numerical results!
MR CFD Support –
Thank you for your positive feedback on the Non-Equilibrium Porous Aluminum Foam Heat Sink CFD Simulation. We are thrilled to hear that our meticulous approach to modeling and the detailed results have been useful and impactful. Your recognition motivates us to continue delivering high-quality simulations and validations. If you have any further questions or need detailed insights into another aspect of our simulation studies, feel free to reach out.
Aglae Turner –
I was impressed by how meticulously the porous aluminum foam heat sink simulation matched the reference article. The validation results make me confident in the accuracy of the provided data models. It was particularly helpful to see the Nusselt number correlation to Reynolds numbers which enhances my understanding of the heat transfer efficiency across different flow conditions.
MR CFD Support –
Thank you for your positive feedback. We’re delighted to hear that the accuracy and detail of the simulation results were instrumental in enhancing your understanding. Our aim is always to provide high-quality, validated simulations that can be trusted for educational and research purposes. If you have any further questions or need assistance with similar simulations, please do not hesitate to get in touch.
Prof. Cheyenne Greenholt –
The description is comprehensive, but could you please elaborate on how the simulation accounted for the temperature non-equilibrium in the porous region? It’s often a tricky aspect to model accurately.
MR CFD Support –
In the simulation, a non-Equilibrium thermal model was employed to accurately capture the temperature differences between the solid matrix and the fluid within the porous aluminum foam region. To do this, specific parameters such as the interface zone density (Hsf) and the heat transfer coefficient (Asf) were defined based on the relationship Hsf.Asf(Ts-Tf), as stated in the article that the simulation is validated against. This approach ensures that the heat transfer between the solid and fluid phases is computed considering the unique conditions of the porous medium thus allowing for an accurate representation of the temperature non-equilibrium situation.
Verla Purdy –
I’m impressed by how closely this CFD simulation aligns with the research paper’s results. Can you share some details on how the Nusselt number was accurately obtained in various Reynolds numbers conditions?
MR CFD Support –
Thank you for the positive feedback! The Nusselt number in the simulation was obtained by carefully setting up the computational model to replicate the conditions in the research paper. The simulation framework involved precise definition of the flow domain, accurate specification of inlet flow properties, and meticulous representation of material properties of the aluminum foam and fin. Special attention was given to specific parameters that affect heat transfer within the porous region, ensuring that corroborating with the graphical data from the research paper was achieved. Each data point for the Nusselt number computations was cross-referenced with corresponding Reynolds numbers to validate our numerical work against experimental evidence.
Prof. Jaleel Huels –
Does the MR CFD product provide suggestions for improvements or alternative configurations for the heat sink based on the results of the simulation, or is it just a validation study?
MR CFD Support –
The MR CFD product focuses on validating the CFD simulation results with the corresponding article. It is primarily structured to show how accurate the simulations are when compared with empirical or experimental data. Therefore, it does not inherently include suggestions for improvements or alternative configurations. However, users may be inspired to conduct further exploration for optimization based on the validation outcomes.
Miss Bernice O’Kon PhD –
I’m absolutely thrilled with how this simulation mirrored the paper’s data! Can you explain how the non-equilibrium option affects the simulation results in contrast to an equilibrium model?
MR CFD Support –
The non-equilibrium model accounts for the temperature difference between the solid and fluid phases in the porous medium, allowing for more accurate analysis when these phases are not in thermal equilibrium. In contrast, an equilibrium model assumes instant thermal balance, which can oversimplify the physics in scenarios where the heat transfer between phases is not instantaneous. This can affect the transient response and thelocal temperature gradients within the porous medium.