Dust Shaped Optimizing Structures for Minimal Drag by ANSYS Fluent

Description

Optimizing Dust-Shaped Structures for Minimal Drag

Project Description:

In this project, a specific dust-shaped geometry that is exposed to wind is simulated and optimized. Simulations aim to investigate the relations between three different input parameters, including their rotation about the 2 axis and inlet velocity magnitude, and their effect on the drag force acting on the object.

Geometry & Mesh:

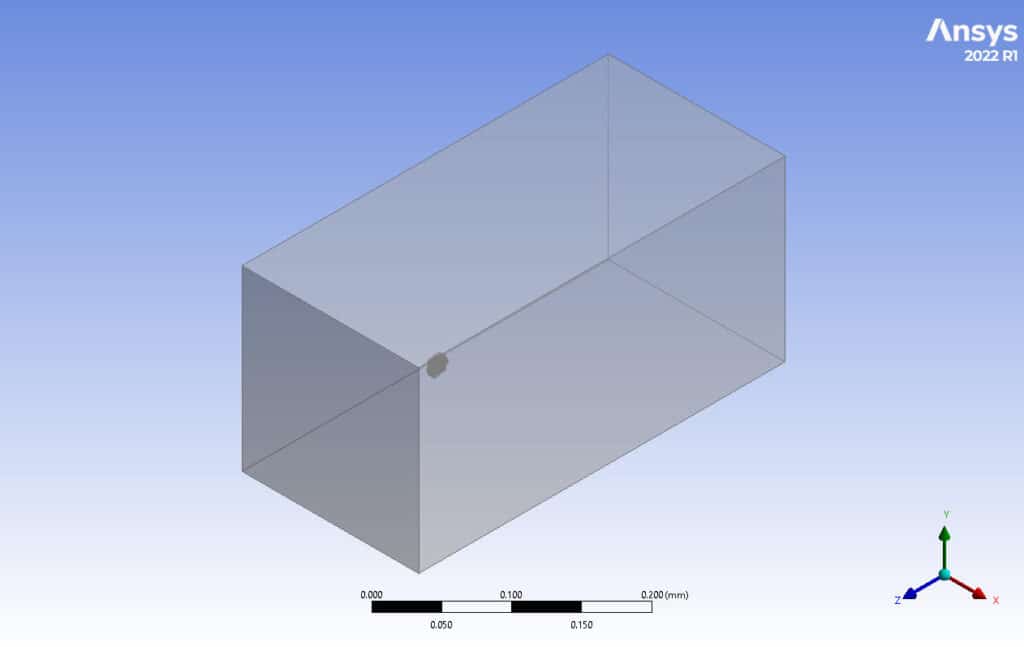
The geometry of the dust shape was created in Ansys Design Modeller & Spaceclaim. An object on a micrometre scale is located in a rectangular cuboid domain (Fig.1). Also, the mesh grid is carried out using Ansys Meshing software. Due to the complexity of the Dust’s geometry, the element size and growth rate, and inflation of the grid about the object are of the essence. As a result, about 3.52 million elements were generated in each case, as can be seen in Figure 2.

Figure 1 – Geometry of the simulation

Figure 2 – Mesh grid and its distribution

CFD Simulation:

The pressure-based solver type is used due to the incompressibility of the working fluid, which is air. In addition, not all of the variables are dependent on time; In other words, the simulation is Steady. As required, the density equals 0.6 kg/m^3 & viscousity has changed to 1.85e-5. Furthermore, the fluid regime is expected to be turbulent, and to capture its behaviour accurately, the K-epsilon Realizable model has been used.

Optimizing:

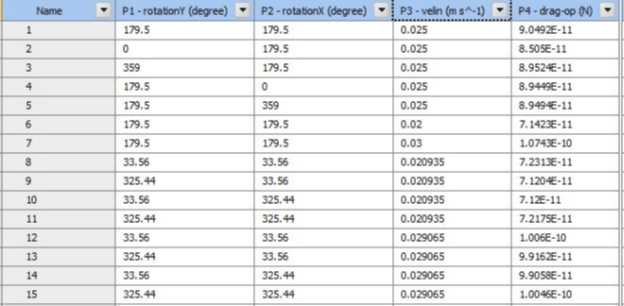
To investigate the impact of inlet velocity magnitude, rotation about the Y-axis, and X-axis on drag force, a Design of Experiment (DOE) along with the Central Composite Design (CCD) method is used. Therefore, 15 different design points are shown in Figure 3.

Figure 3 – Table of design points

Results:

After the simulation and optimization of the dust, 2D contours and different response surfaces are extracted. As can be seen in the below contours(fig.4), the pressure distribution around the object is very smooth because the projected area of it is very small. So the viscous drag is dominant in our problem, and the pressure drag has less impact.

Figure 4 – The streamlines, velocity vectors, and pressure distribution around the object

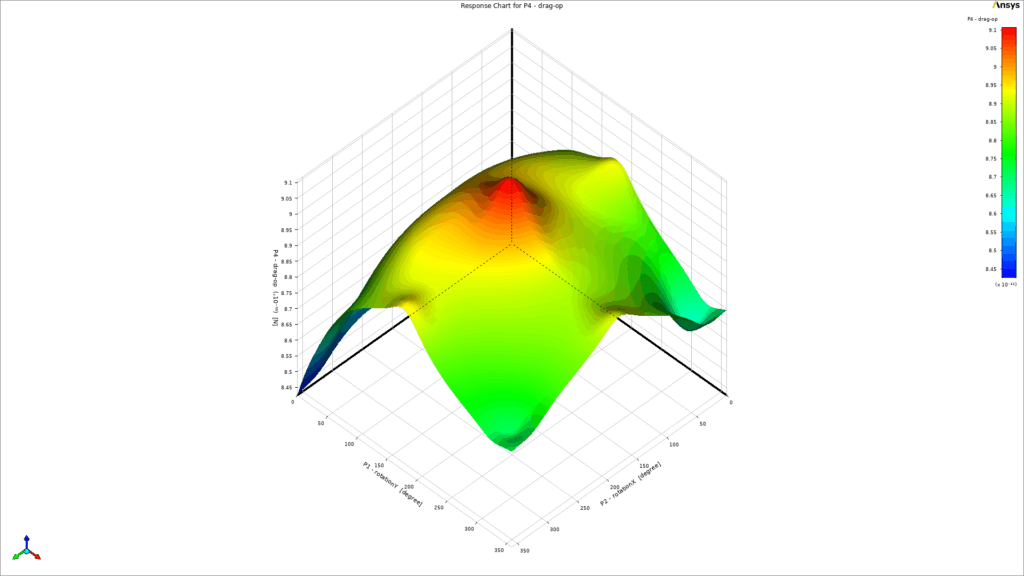
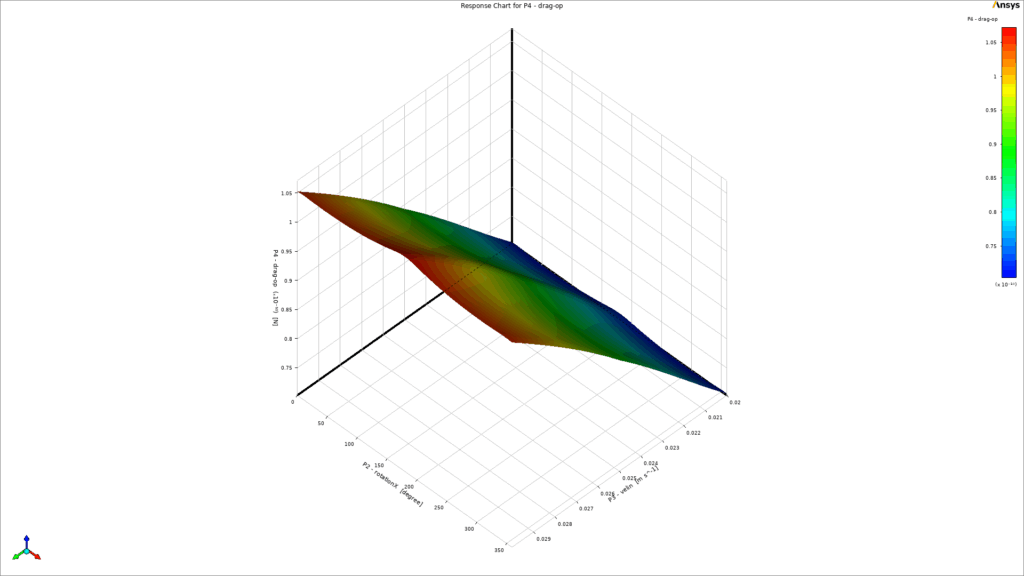
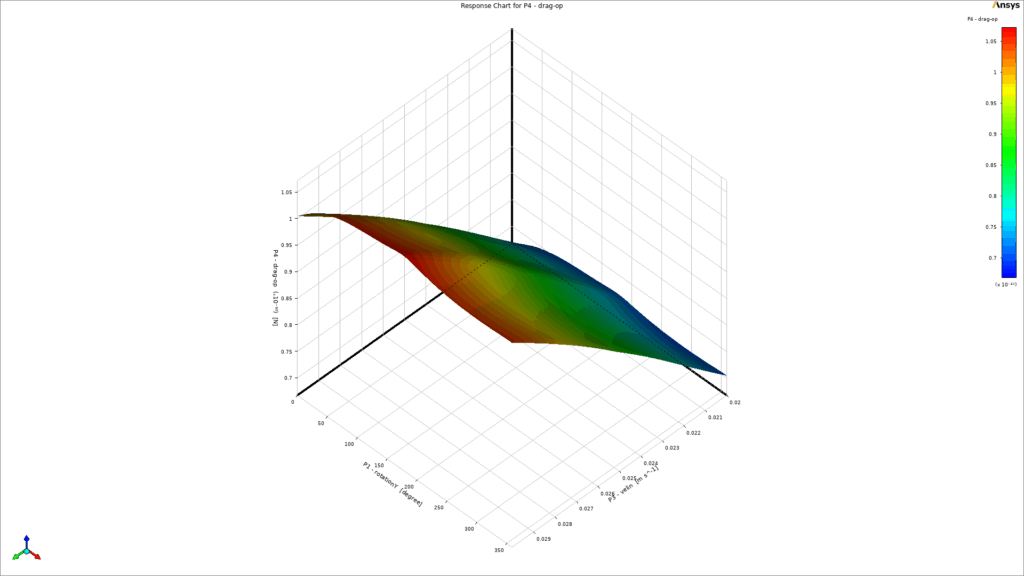
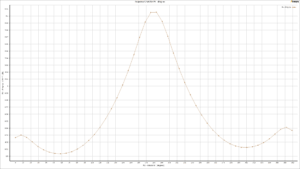
As a key part of the post-processing step, 3-dimensional response surfaces are depicted in Figure 5. They can be very helpful to get a general idea about each parameter`s distribution. To get into more details, 2D plots are extracted (Fig.6). It is clear that the inlet velocity magnitude is the most influential parameter on the drag force acting on the object, and there is a direct relation between them. On the other side, the impact of rotation about the Y-axis could be more effective than rotation about the X-axis (Fig.6d). Therefore, we need to consider all 3 input parameters at the same time to get to the maximum and minimum value of drag force. Thanks to the DOE method of Ansys Workbench, the final report has shown 6.687e-11 and 1.0517e-10 as the minimum and maximum value of drag force, respectively. Figure 7 clearly shows that they had taken place.

A

B

C

Figure 5 – a) 3D response surface of rotation about X-axis, Y-axis, and drag force, b) 3D response surface of rotation about X-axis, velocity inlet

and drag force c) 3D response surface of rotation about the Y-axis, velocity inlet, and drag force

Figure 6 – a) rotation about the x-axis & drag force, b) rotation about the y-axis & drag force c) inlet velocity & drag force, d) local sensitivity of parameters  Figure 7 – maximum & minimum drag force