Shock Wave in a Supersonic Airflow, Transient Solver
$120.00 Student Discount
- The problem numerically simulates Shock waves in a Supersonic Airflow using ANSYS Fluent software.
- We design the 3-D model by the Design Modeler software.
- We Mesh the model by ANSYS Meshing software, and the element number equals 4466857.
- We perform this simulation as unsteady (Transient).
- We use the Density-Based solver to define the compressible flow.
Click on Add To Cart and obtain the Geometry file, Mesh file, and a Comprehensive ANSYS Fluent Training Video.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Shock Wave in a Supersonic Airflow with Transient Solver, ANSYS Fluent CFD Simulation Training
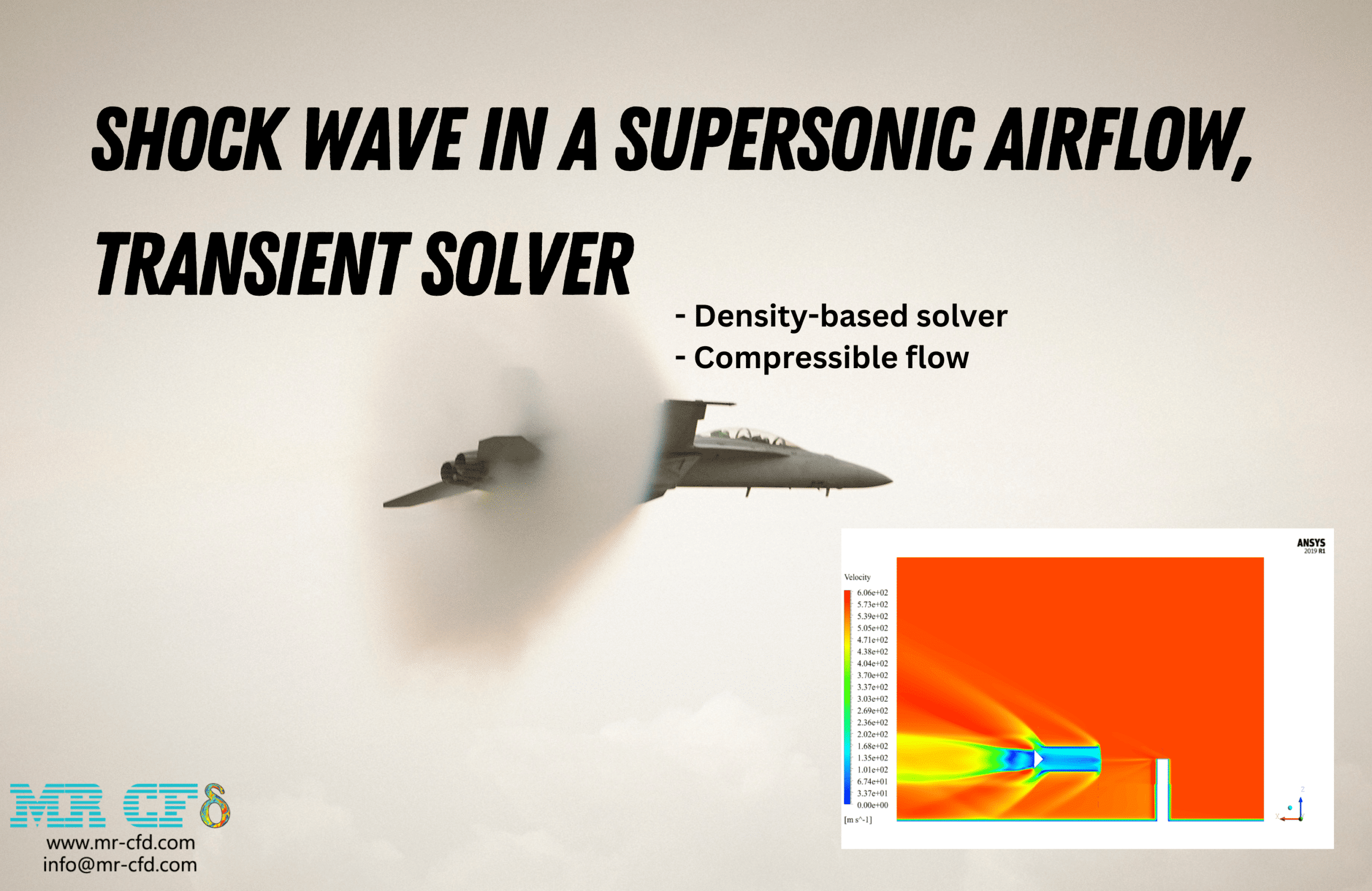
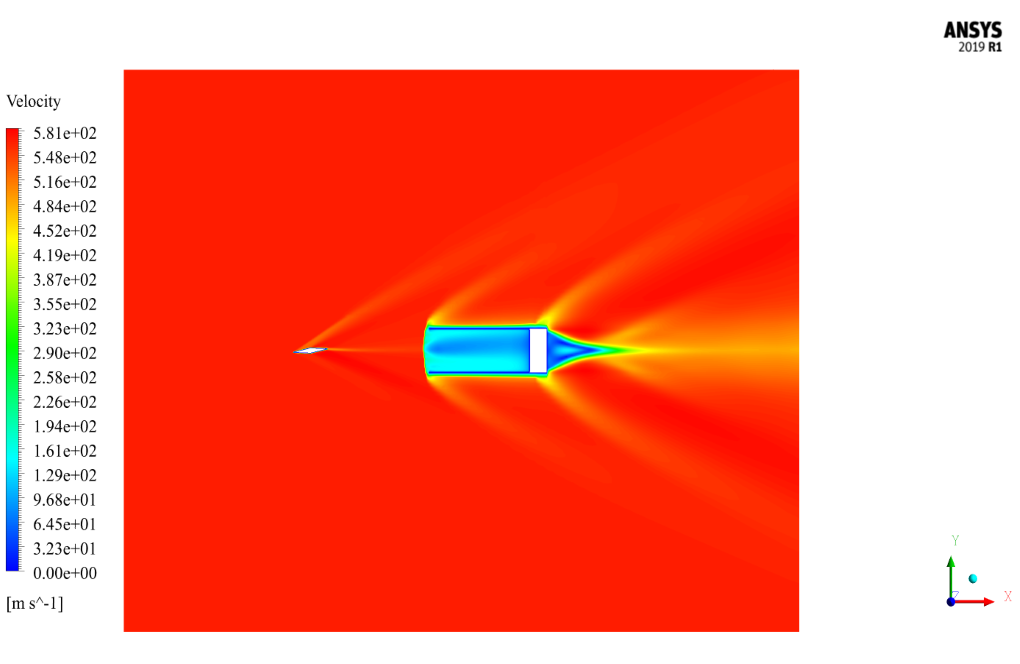
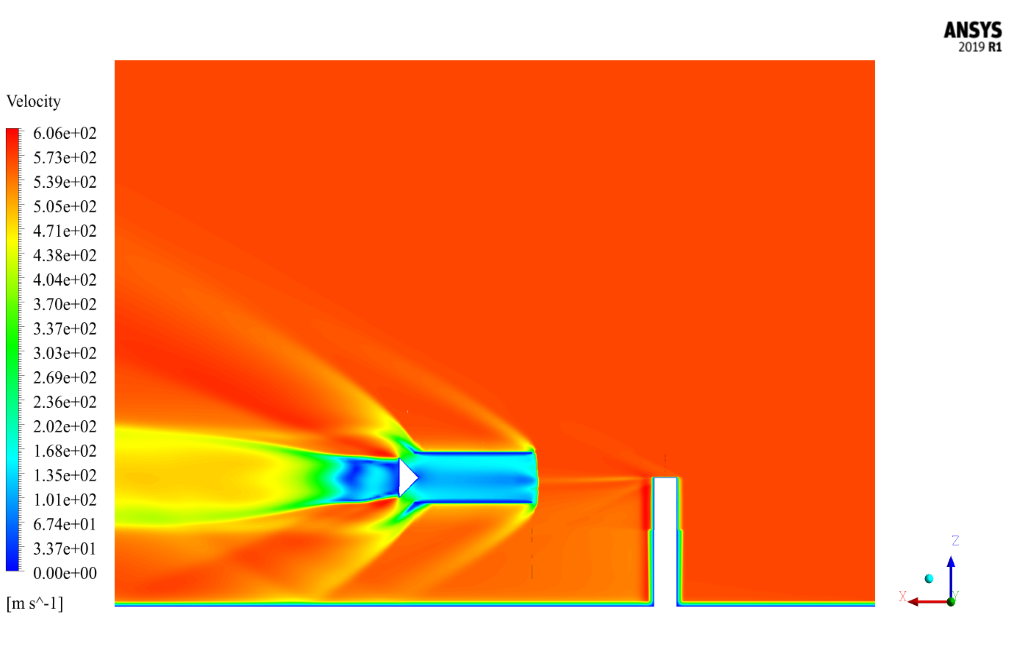
The problem is to simulate the supersonic airflow encountered by a two-way oblique airfoil barrier passing through a channel. So, we investigate fluid behavior and create a Shock Wave phenomenon by ANSYS Fluent software. We perform this CFD project and investigate it by CFD analysis.
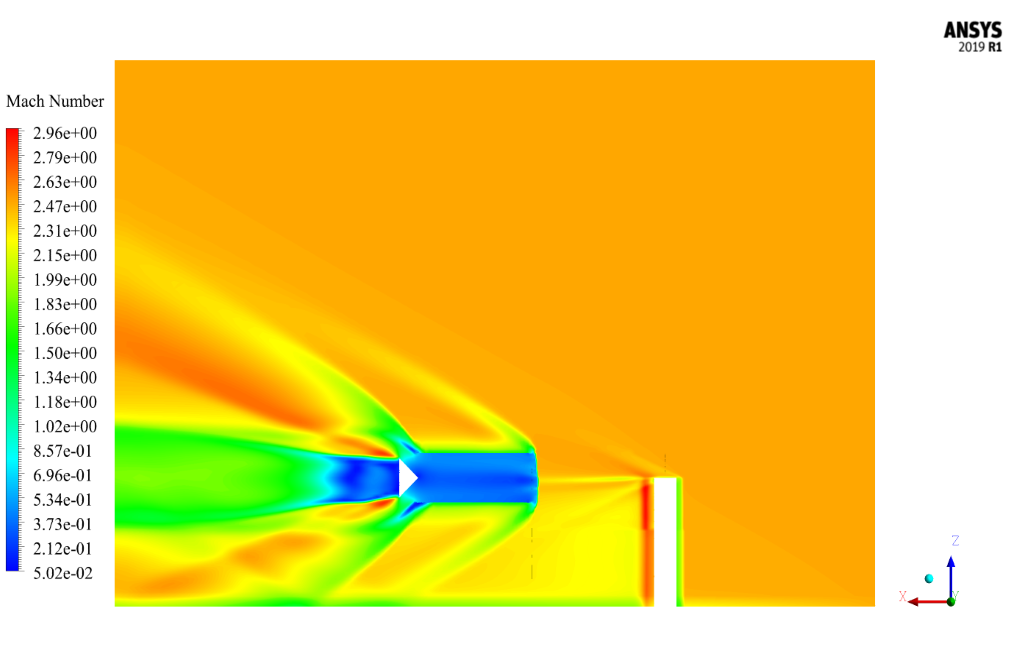
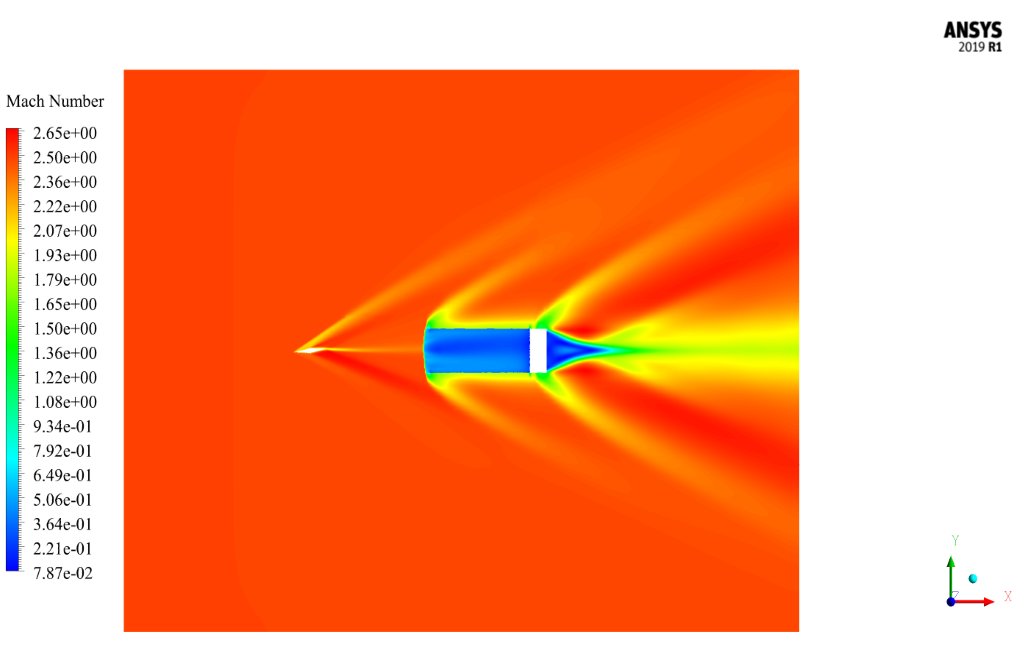
The airflow in the simulation environment around the obstacles and canals has a temperature of 129.46 Kelvin and a Mach number of 2.49. The airflow direction is generally assumed to be in the same direction.
Mach number is a non-dimensional number that indicates the ratio of fluid velocity to sound velocity in the same fluid. This number is usually used when the velocity of the fluid flow is close to the sound velocity or more, and one of the major uses is aerospace applications.
We design the present 3-D model using the Design Modeler software. Then we mesh the present model using ANSYS Meshing software. The mesh type is unstructured, and the element number is 4466857.
Shik Wave Methodology
We use the Density-Based solver to define the compressible flow. In the shocking phenomenon, the airflow is considered quite compressible, and the Mach number is significantly high. It should be noted that the present problem is done in an unsteady state.
Shock Wave Conclusion
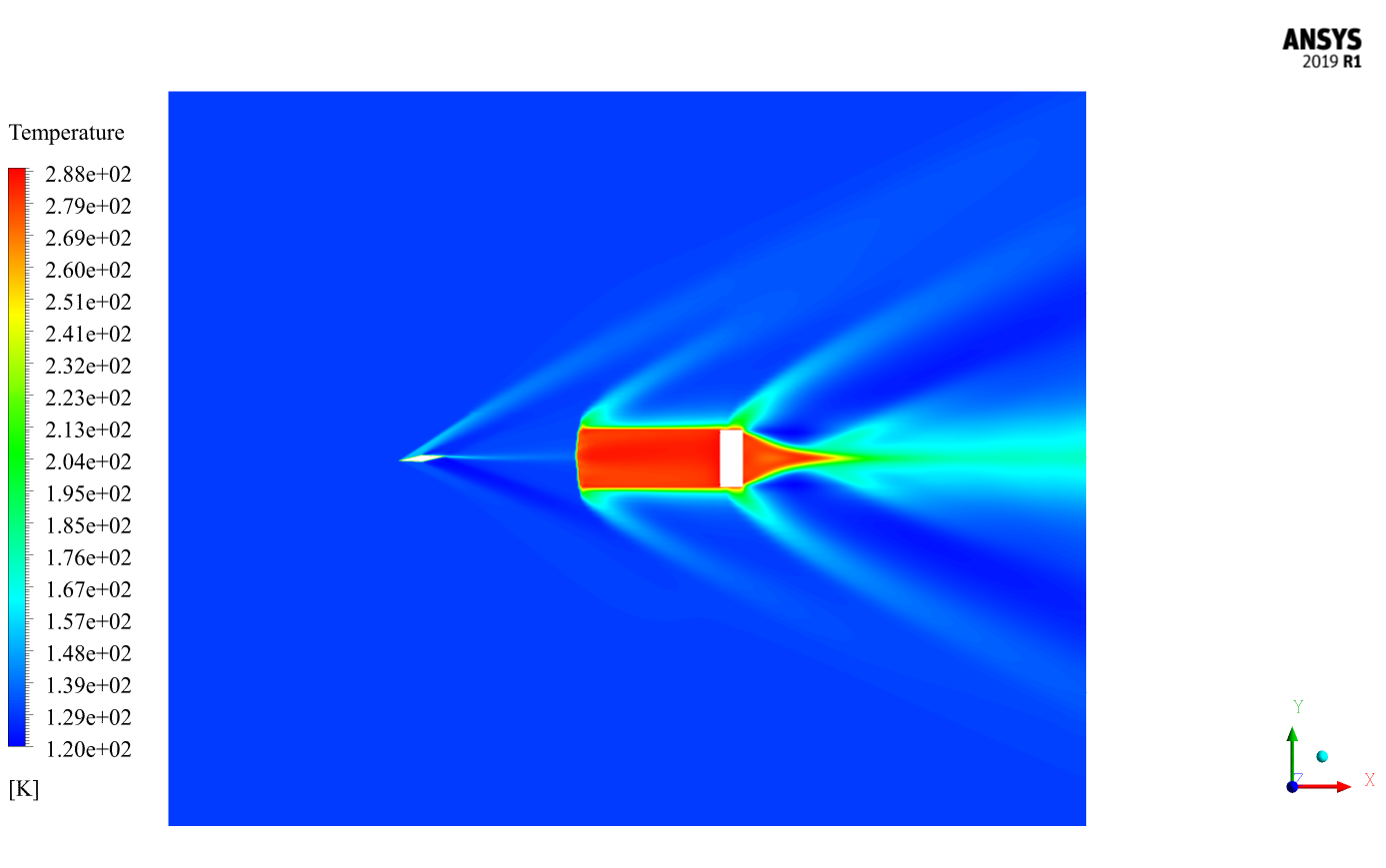
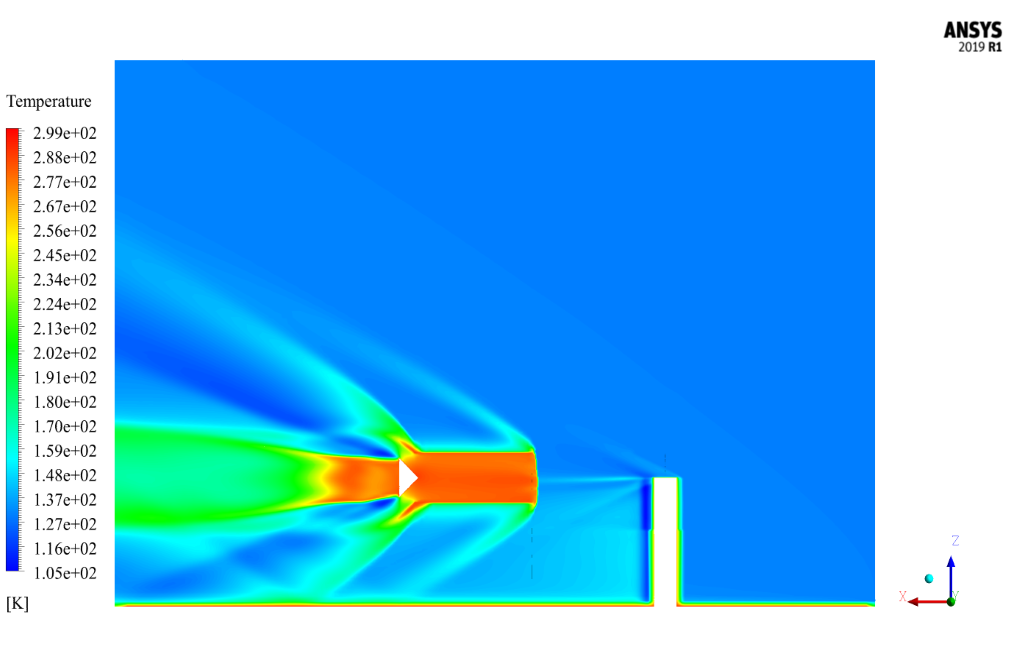
After the solution process is complete, we obtain two-dimensional and three-dimensional contours of pressure, temperature, velocity, density, and Mach number, as well as two-dimensional and three-dimensional pathlines.
We obtain the resulting contours and pathlines in the final second of the unsteady simulation process.
The results show that the shock is well formed. The shock occurred when the current collided with the sharp points of the geometry, and the Mach number changed abruptly. Pressure changes in the shock formation areas of the contours are evident.






Torey Bernier –
Can this simulation be customized to model specific supersonic flow conditions?
MR CFD Support –
Yes, we can accommodate your desired simulations. Please share more details about your specific requirements.
Mrs. Christa Sanford –
Can this simulation be used to optimize the design of supersonic aircraft?
MR CFD Support –
Absolutely! The results from this simulation can provide valuable insights into the shock wave behavior, which can be used for optimizing the design of supersonic aircraft.
Dr. Gust Hill –
The training was excellent and of high quality. I was delighted.
Rosario Walker –
I prepared for one of my university projects and realized what I had to do.
Cecil Osinski –
I’m fascinated by the simulation of shock wave formation in supersonic airflow. What specific challenges are associated with meshing for such high-speed fluid simulations?
MR CFD Support –
Meshing for high-speed fluid simulations, such as the simulation of shock waves in supersonic airflow, involves several challenges. Quality and density of the mesh must be sufficient to capture the steep gradients and discontinuities like shocks. A finer mesh is typically required in areas where shock waves are expected to ensure accuracy of the results. Additionally, maintaining a balance between mesh resolution and computational resources is crucial to perform an efficient simulation.
Gene Okuneva –
I’m thoroughly impressed with the shock wave simulation detailed in your training. The visualization of the shock formation at the airfoil’s sharp points clearly depicts the abrupt changes in Mach number, which is crucial for aeronautics applications. Fantastic job at presenting such a complex phenomenon in an understandable way.
MR CFD Support –
Thank you for your kind words! We’re glad to hear that the simulation was effective in illustrating the shock wave phenomenon and that you found the presentation of the data clear and informative. Your feedback is greatly appreciated, and it motivates us to continue delivering high-quality educational materials.
Kaela Durgan –
I’m thrilled with the results of simulating the shock wave! The contour outcomes illustrating the changes in pressure and temperature were particularly impressive. Thanks for offering such a hands-on learning experience.
MR CFD Support –
We’re overjoyed to hear about your positive experience with the simulation of the shock wave phenomenon. It’s fantastic to know the contour results were instrumental in illustrating the complex changes that occur during shock wave formation. Thank you for your kind words and for choosing our ANSYS Fluent CFD Simulation Training.
Lacey Hill –
I’m impressed by the detailed explanation of the Shock Wave simulation in supersonic airflow! The use of unstructured mesh for handling complex geometries really exemplifies the capabilities of ANSYS Fluent in capturing detailed shock patterns. Great to know the transient solver could accurately predict the shock wave formation around the airfoil barrier. Good work on using a high element count for precision.
MR CFD Support –
Thank you very much for your positive feedback! We’re delighted to hear that you’re impressed with the capabilities of ANSYS Fluent and our efforts in accurately simulating the Shock Wave phenomenon. Precision in CFD simulations, especially for complex aerodynamic events like shock wave generation, is of paramount importance to us. It’s fantastic to know that you appreciate the detail and quality of our work. If you ever have any questions or need further assistance, feel free to reach out. Thanks again for your review!
Darrell Ortiz DDS –
I was fascinated by the detail shown in the generated shock wave graphics. Thanks to MR CFD’s simulation study, it’s become so much easier to visualize complex airflow interactions within supersonic environments.
MR CFD Support –
We are thrilled to hear that our simulation has helped you visualize the intricate details of supersonic airflow interactions effectively. Your appreciation motivates us to continue providing high-quality and insightful simulations. Thank you for your positive feedback!
Mr. Makenna Littel –
The project description was truly enlightening. I could clearly visualize how the airfoil induces a shockwave in a supersonic flow. Excellent material for aerodynamics enthusiasts!
MR CFD Support –
Thank you! We’re thrilled to know that the simulation’s description provided clear insights into the complexities of shockwave behavior in supersonic flows. Your enthusiasm for aerodynamics is precisely what drives us to create detailed and accurate simulation products. If you have any more feedback or need further assistance, feel free to reach out!
Torrance O’Reilly –
The results of the Shock Wave simulation supplement my studies in aerodynamics perfectly—the visualization of high-speed phenomena through CFD is enlightening.
MR CFD Support –
We’re thrilled to hear that our simulation of the Shock Wave in a supersonic airflow was so beneficial for your studies. Thank you for choosing our learning product to assist in visualizing complex aerodynamic events!
Blair Barton –
I’m particularly impressed with the detail in the captured shockwave phenomena and the temperature and velocity distributions presented. The visualisations of the airflow interactions with the oblique airfoil barrier really elucidate the complexities involved in supersonic flow simulations.
MR CFD Support –
Thank you for your kind review. We are delighted to hear that the simulation details and visualisations met your expectations and provided clear insights into high-speed airflow interactions. Quality and clarity in our CFD simulations are priorities for us, and it’s rewarding to know they’ve aided your understanding of supersonic flows.
Hilton Wunsch –
I was impressed by the high Mach number simulation capabilities you described. It’s very detailed and seems extremely valuable for aerospace applications!
MR CFD Support –
Thank you for your positive feedback! We are glad to hear that the details and capabilities of our supersonic airflow simulation with a shock wave were impressive to you. We always strive to provide valuable and precise simulations for all applications, including aerospace. If there’s anything more you’d like to know or another aspect you’re interested in exploring, feel free to reach out to us!
Brian Purdy –
Is it possible to use the same simulation setup for other types of barriers, such as a ramp or a wedge, instead of a two-way oblique airfoil? If so, would the simulation treat the different geometries the same or would adjustments need to be made?
MR CFD Support –
In principle, you can use a similar simulation setup for other types of barriers, such as a ramp or a wedge; however, adjustments would typically be essential to accommodate differences in geometry. These changes could involve modifications to the boundary layers settings, mesh refinement near critical areas, and validation of appropriate flow conditions that accurately represent interactions specific to the new shapes of the barriers.
Prof. Rylee Walsh DDS –
What is the significance of using a Density-Based solver in this simulation, and could a Pressure-Based solver be used instead for shock-wave phenomena?
MR CFD Support –
The Density-Based solver is specifically designed for flows where density changes are significant, such as shock waves in supersonic flow regimes. Unlike the Pressure-Based solver, the Density-Based solver can capture the rapid density changes due to shock waves more accurately, which is crucial for a precise analysis of supersonic flows. While a Pressure-Based solver can be employed in some compressible flow simulations, it is generally less accurate for high-speed flows involving shocks. Its use in such cases might require special settings and considerations.
Prof. Berneice Stanton PhD –
What type of solver did you use—the Density-Based or Pressure-Based solver—and why was it the most suitable one for this simulation?
MR CFD Support –
For this simulation, the Density-Based solver was used because it is well-suited for capturing the high-speed compressible flows that are characteristic of shock wave phenomena. Its capability to handle significant density changes within the flow field makes it ideal for tracking discontinuities like shock waves resulting from supersonic flow interactions with airfoil barriers.
Dr. Brenden Weber –
The visuals and transition of the shock formation were demonstrated very effectively in the simulation results. The distinction between pre-shock and post-shock conditions was particularly well characterized, showcasing the power and accuracy of the simulation tool. Excellent work on creating such a detailed and insightful CFD study!
MR CFD Support –
Thank you for your encouraging feedback! We’re thrilled to know that you found the shock wave simulation insightful and the portrayal of its formation effective. Accurate visualization of such complex phenomena is crucial for understanding fluid dynamics in aerospace applications, and we are glad our product met your expectations. We look forward to providing you with more quality simulations in the future.
Fredy Leffler –
I’m blown away by the detailed investigation on the shock wave using ANSYS Fluent’s Transient Solver. The insights into the supersonic airflow behavior and seeing the well-formed shock in the results are absolutely fascinating!
MR CFD Support –
Thank you so much for your kind words! We’re thrilled to hear that our training on simulating shock wave phenomena in supersonic airflow using ANSYS Fluent has been impressive and insightful. It’s our goal to provide comprehensive CFD simulations that are both educational and engaging. Your feedback motivates us to keep delivering high-quality learning experiences to all our customers.
Ida Tremblay IV –
Can I apply the results from this shock wave simulation to optimize designs in aerospace applications?
MR CFD Support –
Yes, the insight gathered from the shock wave simulation, like the changes in pressure, temperature, and density across the shock, can be very useful for optimizing designs in aerospace applications, especially when dealing with supersonic flows and the associated shock-induced phenomena.
Rogers Rolfson –
The detailed simulation mapping of a shockwave is such an intricate process, but this training seems to nail it! The clear definition of the shock formation and the precise measurement of the changes in pressure and Mach numbers is super impressive.
MR CFD Support –
We’re delighted to hear that our training material on supersonic airflow and shock wave simulation met your expectations and proved insightful! Thank you for recognizing the clarity of our simulation process and the accuracy of our results. Your appreciation motivates us to keep providing high-quality CFD simulation training. Thank you for your review!
Mr. Madison Renner V –
I’m fascinated by how the shock wave forms around the airfoil. Your explanation made it clear how complex the simulation setup must be. Amazing work!
MR CFD Support –
Thank you for your kind words! We’re really glad to hear you found the explanation clear and the topic intriguing. We always strive to provide detailed analyses to help our customers understand complex aerodynamic behaviors. Thank you for taking the time to review our products!
Kieran Kerluke –
I’m astounded by the results, the visualizations make it clear how the shock wave is formed and behaves when it interacts with the airfoil obstacle. Well done on capturing the dramatic changes in Mach number and pressure!
MR CFD Support –
Thank you for your positive feedback! We’re delighted to hear that the visual clarity of the shock wave formation and its underlying physics were well-represented in our simulation training. It’s always encouraging to see our work appreciated, and your compliments serve as a great motivator for us to continue delivering quality simulations. If you have any further insights or need more information, please let us know!
Christian Koepp –
What visualization techniques are utilized for identifying the shock wave phenomena clearly in this simulation?
MR CFD Support –
Advanced visualization techniques such as pressure, temperature, velocity, density, and Mach number contours along with two-dimensional and three-dimensional pathlines are utilized to clearly identify and analyze the shock wave phenomena in the CFD simulation of the supersonic airflow.
Kenneth Dicki –
What steps are taken to ensure the accuracy of the shock wave formation in the context of the mesh and solver settings in this simulation?
MR CFD Support –
To ensure accuracy of the shock wave simulation, fine meshing near the obstacle and in areas where sharp gradients are expected is implemented. The Density-Based solver is chosen specifically for capturing compressible, high-speed flow effectively. Time-stepping is carefully controlled to capture the transient nature of the shock wave formation accurately. Also, verification of the results with expected physical phenomena and convergence checks are integral steps to confirm accuracy.
Mrs. Celestine Spinka –
I’m just blown away by the level of detail in the Shock Wave in a Supersonic Airflow with Transient Solver, ANSYS Fluent training. The results presented, especially the sharp capture of the shock wave and the accompanying changes in Mach number and pressure, are impressive and indicative of high-fidelity simulations. This goes a long way in demonstrating the capabilities of ANSYS Fluent in capturing complex flow phenomena.
MR CFD Support –
Thank you for your kind words. We are thrilled to hear that you are satisfied with the quality and detail of the simulation work, and that you appreciate the capabilities of ANSYS Fluent in showcasing complex aerodynamic phenomena. Your feedback is greatly valued.
Johanna Metz –
The description of this CFD simulation of a shock wave was very detailed. The supplied temperature and Mach number specifics provided a good insight into the process.
MR CFD Support –
Thank you for your appreciation of the shock wave simulation training description. We are delighted to provide detailed information to ensure a comprehensive understanding of our simulations.
Prof. Alessandro Mante –
This project is quite astounding! I’m very impressed by the detailed simulation of the shock wave in the supersonic airflow. The use of an unstructured mesh to capture the high-gradient phenomena like shock waves was a good choice. The comprehensive data provided on pressure, temperature, velocity, density, and Mach number contours is immensely helpful for understanding the flow characteristics around the airfoil. Great job on completing what must have been a complex and computationally intense simulation.
MR CFD Support –
We truly appreciate your positive feedback on our simulation of the shock wave in a supersonic airflow. It’s exciting to hear that the level of detail and the results presented have met your expectations. Understanding such complex phenomena is pivotal, and we strive to provide the best insights with our CFD simulations. Thank you for choosing our training product and for taking the time to leave your review. If you ever have any more detailed inquiries or need further assistance, feel free to reach out!
Tiffany Wehner –
I’m impressed by the detailed analysis of shock wave formation in a supersonic airflow environment. One can appreciate the precision put into the simulation setup, mesh generation, and the use of a density-based solver to cater to high Mach numbers and compressibility of the flow. The final visualization of the shock wave is a testament to the capabilities of the ANSYS Fluent software and your expertise in handling complex aerodynamic simulations.
MR CFD Support –
Thank you for your kind words and for recognizing the effort that went into this simulation! We are thrilled that you found the details and final visualizations impressive. Our goal is to provide comprehensive and realistic CFD simulations to help understand intricate fluid dynamics phenomena like shock waves. Your satisfaction with our training product validates our dedication to high-quality simulations and instructional materials. Thank you once again for the positive feedback!
Keshawn Langosh –
Exceptional learning experience! The details on the shock wave formation and the use of numerical methods to analyze supersonic flows were incredibly insightful. The iteration through contour and pathline results made it much easier to comprehend the shock wave phenomenon.
MR CFD Support –
We’re thrilled to hear that the content provided you with a comprehensive understanding of shock wave dynamics in supersonic airflow and that the visualization through contour and pathlines was helpful. Thank you for your positive feedback!
Prof. Hermina Walker Sr. –
I’m super impressed with the depth of the results from the shock wave simulation. The visualization of complex phenomena like shock formation and the abrupt changes in the Mach number are fantastic!
MR CFD Support –
Thank you for your positive feedback! We are delighted to hear that you are impressed with the results and visualization of the shock wave simulation. Our team strives to provide accurate and detailed simulations, and it is rewarding to know when our efforts make a difference. If you have any questions or need further information on our products or simulations, please feel free to ask.
Jose Wyman –
I’m fascinated by the shock wave phenomenon captured in this simulation. Could you explain what happens to the pressure and temperature across the shock wave? How do they change on moving from subsonic to supersonic conditions across the shock wave?
MR CFD Support –
In the simulation of the shock wave, when airflow transitions from subsonic to supersonic across the shock, there’s a sudden increase in pressure and temperature. Essentially, the kinetic energy of the fast-moving air is converted into thermal energy, leading to these increments. As the air passes through the shock wave, the Mach number drops below 1, indicating a change from supersonic to subsonic conditions. The airflow also decelerates, and its dynamic pressure is converted into static pressure, leading to the observed changes.
Prof. Nikki Cremin IV –
I am amazed to see the shock wave formation in the simulation. The results are visually striking, and I appreciate how well the simulation captures the abrupt changes in Mach number. The details in pressure, temperature, and density changes provide a great and easy-to-understand insight into how shocks behave in supersonic flows.
MR CFD Support –
Thank you for your positive feedback! We’re delighted to know that our simulation provided you with a clear understanding of the shock wave phenomenon in supersonic flows and that you found the visualization of the changes in different flow properties insightful. Your compliments really inspire us to continue delivering high-quality CFD simulations. If you have any more questions or need further information regarding our learning products, please feel free to reach out!
Mia Macejkovic –
The training for the Shock Wave in a Supersonic Airflow simulation was informative. I could see how the shock wave was generated and how the Mach number changed across the model. Great job demonstrating the shock phenomenon using ANSYS Fluent!
MR CFD Support –
Thank you for your positive review! We’re glad that you found the training on the Shock Wave in a Supersonic Airflow informative and that the CFD simulation using ANSYS Fluent met your expectations. If you have any more questions or need further assistance, please feel free to reach out.
Patience Wilkinson –
I’m fascinated by the simulation of a shock wave in a supersonic airflow! Can the density-based solver handle the transmission and reflection of shock waves over time and distance accurately?
MR CFD Support –
Yes, the density-based solver in ANSYS Fluent is specifically designed to handle compressible flow regimes where shock waves are present. It accurately captures the transmission and reflection of shock waves over time and distance by solving the conservation equations for mass, momentum, and energy simultaneously.