Geothermal Reservoir CFD Simulation, ANSYS Fluent Tutorial
$120.00 Student Discount
- The problem numerically simulates the geothermal reservoir using ANSYS Fluent software.
- The 3-D model is designed in Design Modeler software.
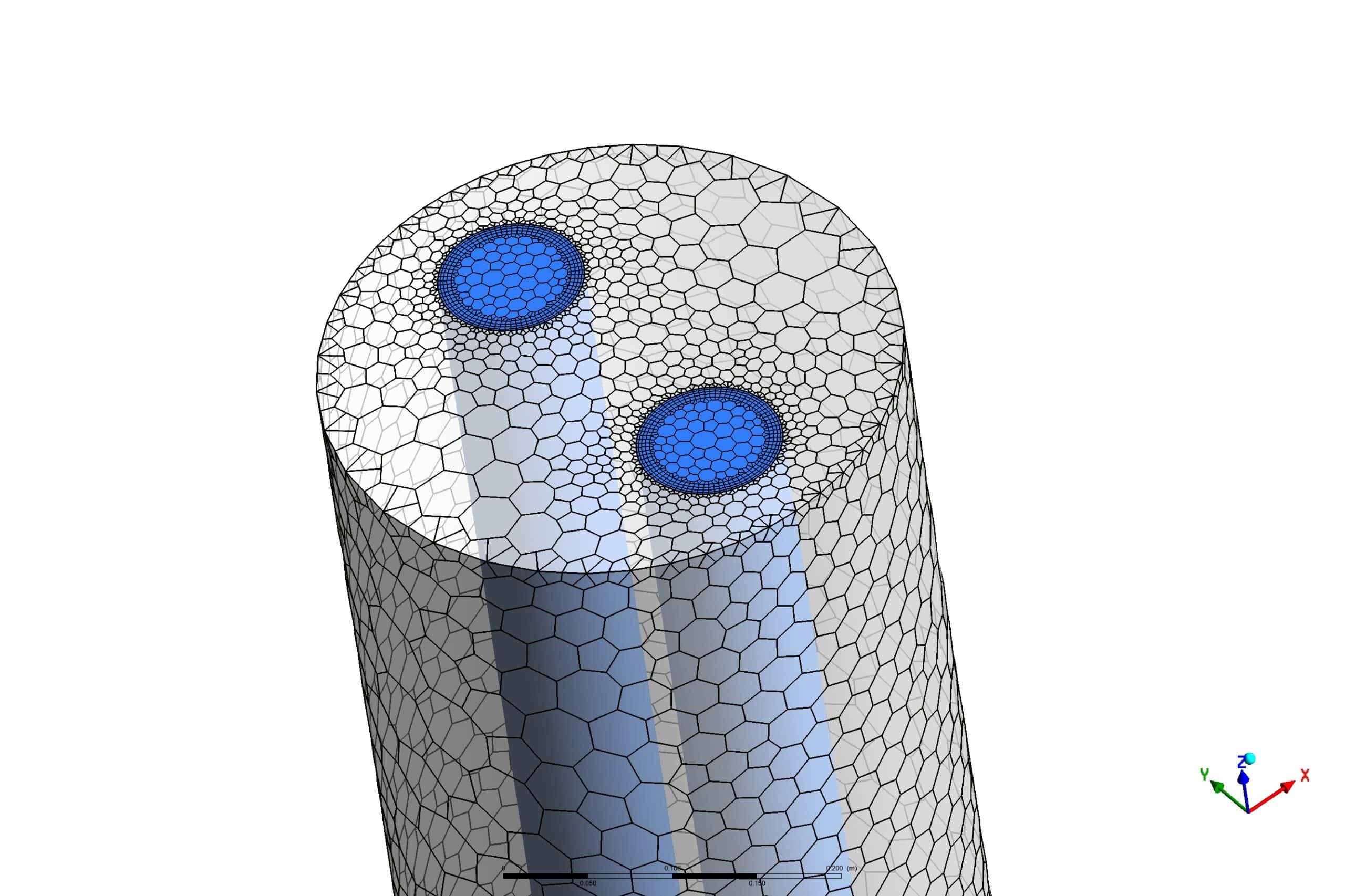
- We mesh the model with ANSYS Meshing, and the element number equals 1,749,097.
- We use the Realizable k-epsilon model to simulate turbulence.
- Conductivity and heat capacity are considered temperature-dependent.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Description
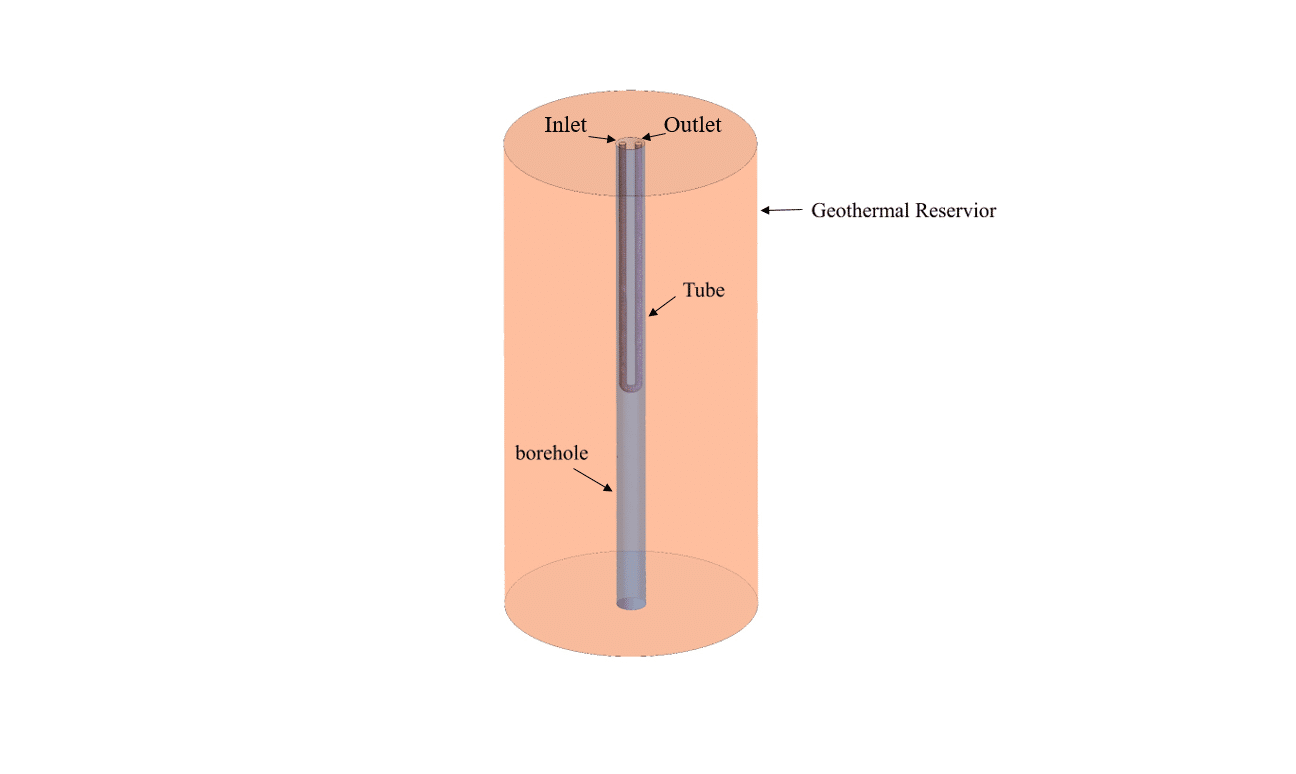
This project aims to simulate a geothermal reservoir using a single U-tube, a Downhole heat exchanger (DHE), which consists of a system of tubes or a U-tube located in a single wellbore, through which the working fluid is circulated to extract heat.
The simulation model is based on a small-scale field case and consists of three parts: the U-tube, borehole, and ambient geothermal reservoir. In an actual situation, the process occurs 200 meters under the ground. We scaled the model in which the depth of the ground zone and u-tube is 6 and 3.2 meters, respectively.
We designed the U-tube with an inlet and outlet diameter of 0.0875 meters. It is surrounded by a borehole of 0.35 diameter and 6 m height inside the ground zone, a cylinder with a diameter of 3 m.
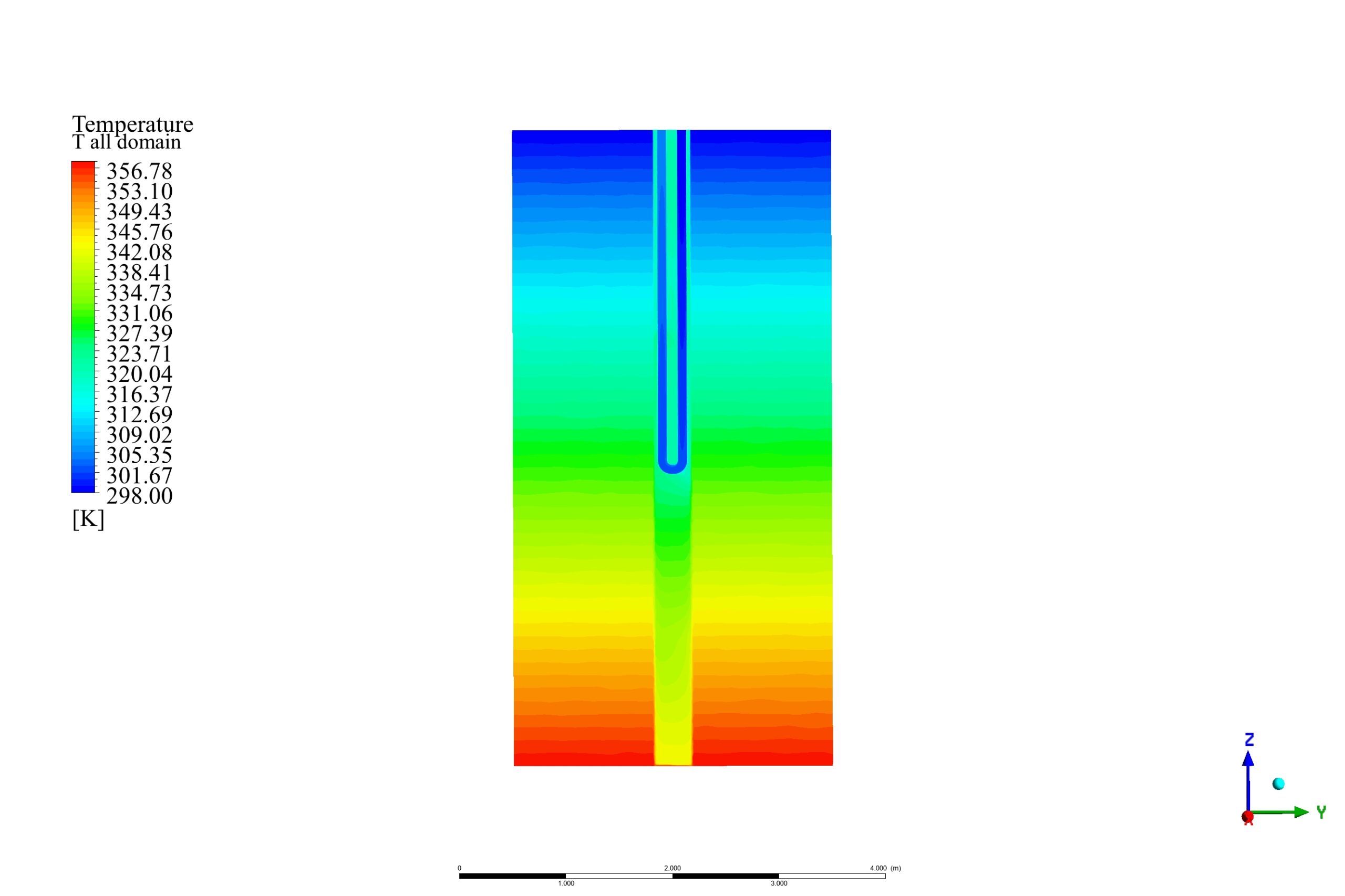
In the solid zone, the temperature varies linearly from top to bottom, which makes the hole temperature change the same way. This causes free convection heat transfer, and the heat is extracted from the ground and transferred to the tube so that the outlet temperature of tube water increases.
The temperature of the solid zone is defined as a linear function of temperature in Named Expression.
We modeled the geometry of the project using Design Modeler software. Then we meshed the model with ANSYS Meshing software. The mesh model is polyhedra, and the number of cells equals 1,749,097.
Geothermal Reservoir CFD Simulation Methodology
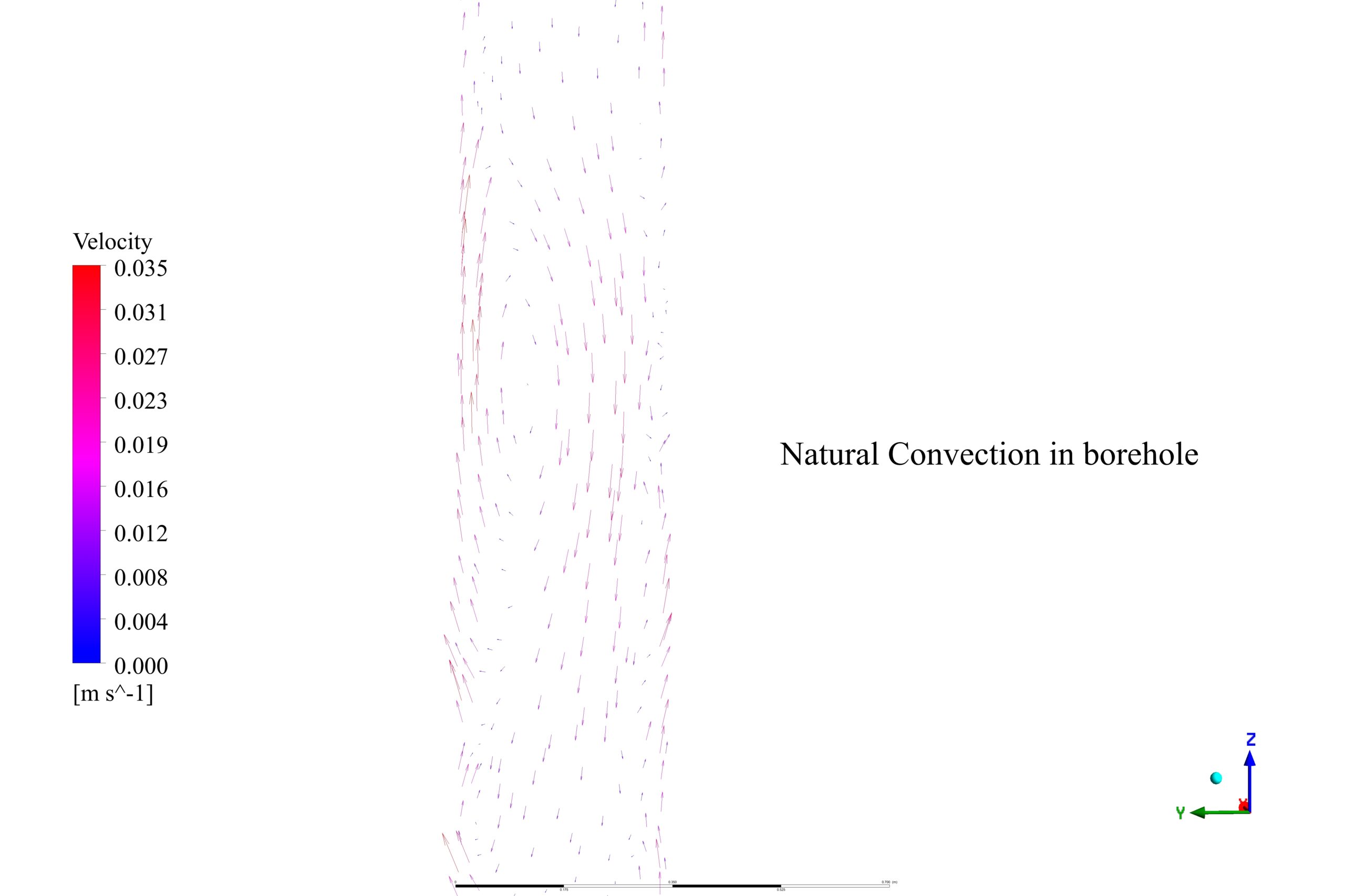
In this project, we consider gravity since the water inside the hole moves due to natural convection. It takes the heat from the bottom of the hole and gives it to the pipe and the water flowing inside.
In order to simulate the turbulence of the fluid, we used the Realizable k-epsilon model with a standard wall function.
The polynomial method defines water heat conductivity and heat capacity as temperature-dependent. The flow behavior is steady.
Conclusion
After the solution, we obtained the contour of temperature, pressure, and velocity vectors for tube and hole zones.
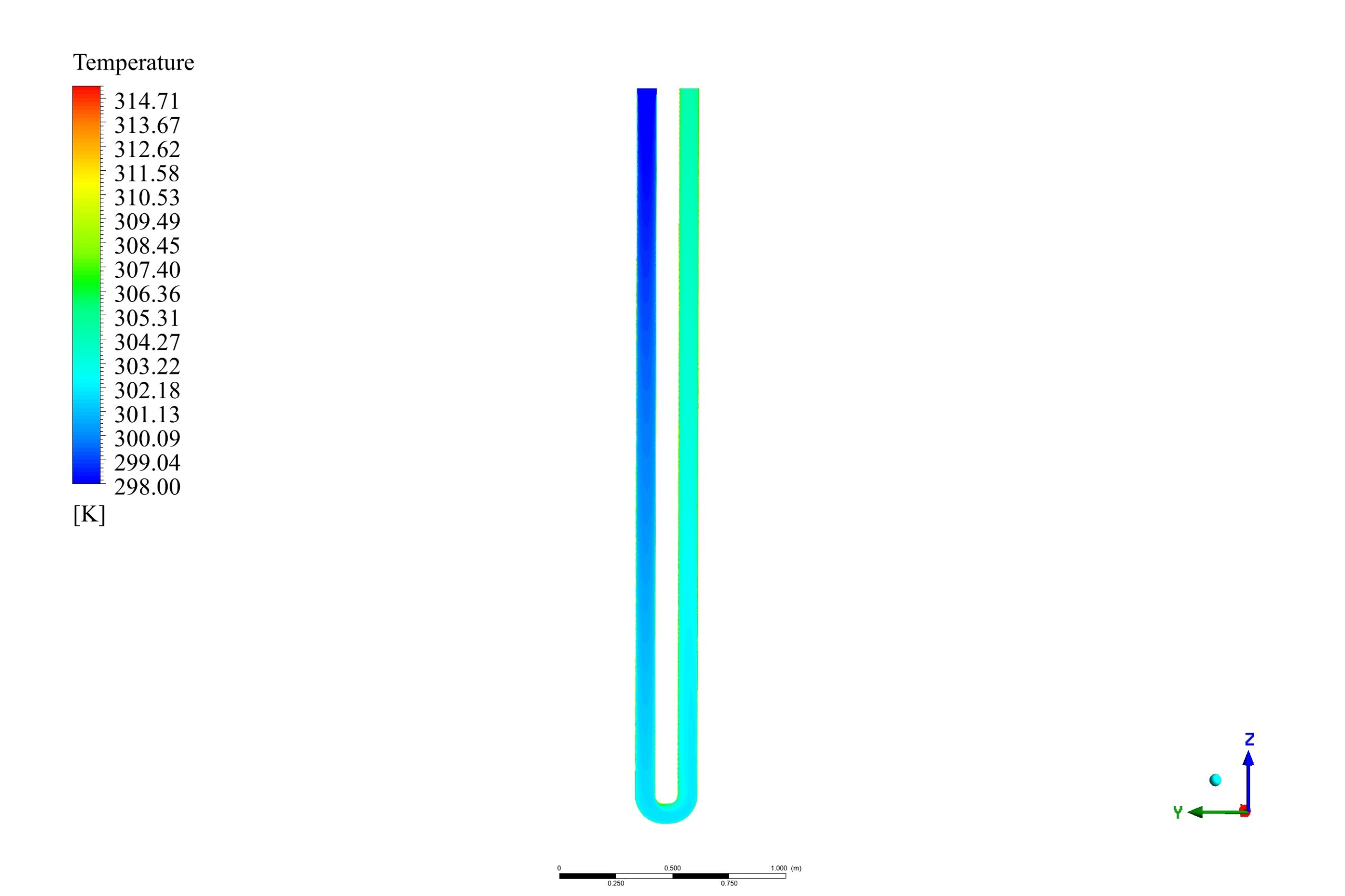
The results show that the convective heat transfer between the hole and the tube increases the tube outlet temperature to 305.47 k.
As the velocity vectors show, the generated vortex at the bottom of the hole consequently increases flow turbulence and heat transfer. Since the temperature of water flow near the wall increases, its density decreases, so it goes up and transfers the heat to the upper layers of water. Its temperature decrease and comes back down; natural convection happens, and heat is transferred to the tube.


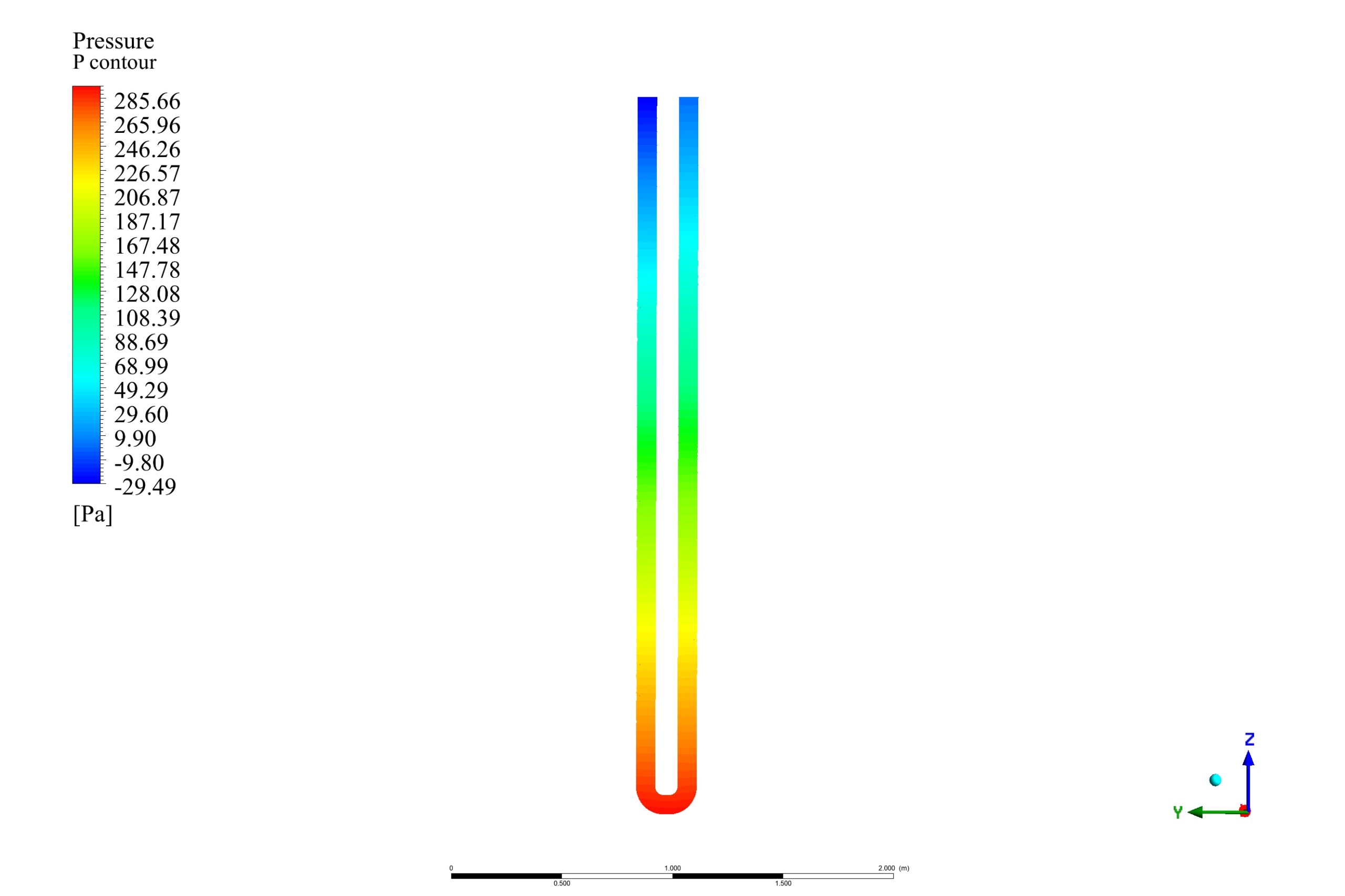

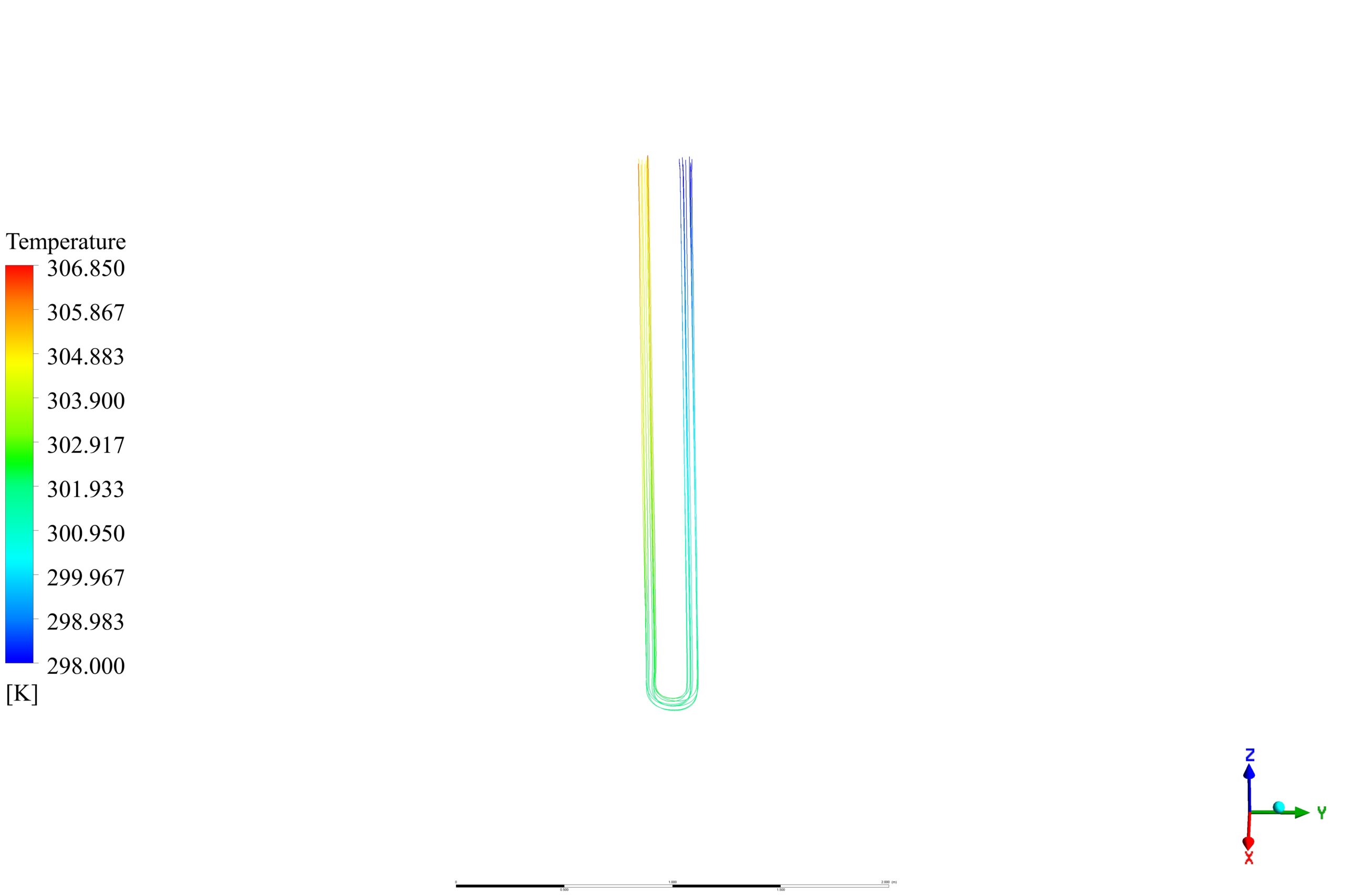




Willis Strosin I –
I appreciated learning about the Geothermal Reservoir CFD simulation process. The use of the Realizable k-epsilon model and the visualization of convection patterns were enlightening. Fantastic work on explaining the phenomenon so clearly!
MR CFD Support –
Thank you for your kind words! We’re thrilled that our Geothermal Reservoir CFD simulation tutorial was able to provide you with clear and insightful information. Your feedback is incredibly valuable to us. If you have any further questions or need additional clarification, please don’t hesitate to reach out. We love hearing from our customers!
Carrie Kreiger –
What specific aspects of the geothermal reservoir’s physical properties were most critical in influencing the outcomes of the simulation?
MR CFD Support –
The key physical properties that critically influenced the outcomes of the simulation included the thermal conductivity and heat capacity of the water, which were modeled as temperature-dependent. Additionally, the temperature gradient within the solid zone, which dictates the heat transfer by free convection from the ground to the U-tube, played a critical role.
Dayna O’Hara –
The tutorial for the Geothermal Reservoir CFD Simulation was very insightful. How accurate is this simulation for predicting real-world geothermal reservoir behavior?
MR CFD Support –
The simulation is scaled and designed to closely resemble real-life conditions using physics-based models, thus providing a reasonably accurate representation of geothermal reservoir behavior. However, real-world conditions may introduce complexities that are not captured in the simplified model, so while the simulation can provide useful insights and predictions, actual site-specific data is needed for precision in real-world applications.
Sabrina Robel –
This Geothermal Reservoir simulation is splendid! The detailed explanation really helps appreciate the complexity and the accuracy of the CFD model. Great work on scaling the model accurately and achieving natural convection representation.
MR CFD Support –
We’re thrilled to hear you’re so pleased with our Geothermal Reservoir simulation! It’s fantastic to know that our efforts in scaling and accurately modeling natural convection have enriched your understanding. Thank you for your positive feedback!
Kaela Carroll Sr. –
The tutorial and simulation outcomes for the geothermal reservoir were phenomenal! I truly appreciated the depth of detail in methodology and the clear visualization of the temperature gradients, pressure distribution, and flow patterns. It significantly enhanced my understanding of the geothermal heat exchange process within the U-tube system. Thank you for an insightful and invaluable learning experience.
MR CFD Support –
Thank you for your positive feedback! We are thrilled to hear that our simulation materials have provided you with a comprehensive understanding of the complex processes involved in a geothermal heat exchange system. Your intellectual growth is our greatest reward, and we look forward to supporting your educational journey further.
Olga Nader –
I’m blown away by the complexity of this project. Your team’s ability to model geothermal energy extraction using CFD is truly impressive. The level of detail in the simulation methodology provides great insights into the heat transfer process, and the outcomes with natural convection effects are exciting. It certainly opens up opportunities for optimization in renewable energy technologies. Terrific job!
MR CFD Support –
Thank you so much for your enthusiastic review! We’re thrilled to know that you appreciate the intricate work involved in this geothermal simulation project. Our team strives to deliver detailed and accurate simulations to help understand and improve renewable energy technologies. Your recognition of our efforts is very motivating for us. Should you need any further details or assistance, don’t hesitate to reach out. Thanks again for your support!
Dr. Hayley Russel DVM –
The tutorial for the geothermal reservoir looks detailed, but can it be done at larger depths typical for geothermal projects, such as over 1,000 meters?
MR CFD Support –
The simulation tutorial provided has been scaled down for instructional purposes. However, the same principles and methodologies can be applied to model full-scale scenarios at larger depths, such as over 1,000 meters, by adjusting the domain size and boundary conditions to match the conditions found deeper underground.
Zula Swift –
I’m impressed with the detailed analysis and results. The concept of using natural convection in a geothermal setting sounds fascinating. Can you tell me if this type of system is scalable for larger operations?
MR CFD Support –
Thank you for your kind words and interest in our geothermal reservoir simulation product. In response to your question, yes, the principles found in our simulation study are scalable. Actual geothermal systems that use U-tube configurations operate similarly and have been successfully scaled to meet the demands of larger operations. The concepts modeled in the simulation reflect real-world physics and can be adapted to different sizes and capacities to suit the requirements of larger geothermal energy projects.
Trycia Schimmel –
Tremendously informative material! Has the Realizable k-epsilon model shown a marked difference in predictability of turbulence over simpler models, within the context of this geothermal simulation?
MR CFD Support –
Thank you for your positive feedback! Our decision to use the Realizable k-epsilon turbulence model in this geothermal simulation stems from its enhanced capacity to handle the impact straight and swirling flows have on turbulence predictability compared to simpler models. This sophistication is particularly useful in accurately depicting the natural convection effects and the resulting turbulence in the reservoir, which is key to a successful heat exchange analysis.
Dr. Casimer Reinger II –
I found the explanation of how a geothermal reservoir system works so interesting! The data presented after the simulation gives a great insight into the practical aspects of geothermal energy extraction.
MR CFD Support –
Thank you for your kind words! We’re glad to hear that you found the geothermal reservoir simulation useful and insightful. It’s always our goal to present our findings in a way that’s both informative and relevant to real-world applications. Should you have any further interest in our projects or any questions, we’re here to help.
Melba Casper –
I’d love to know more about the characterization of the geothermal reservoir. How does the simulation take into account the varying properties of the geological layers?
MR CFD Support –
The characterization of the geothermal reservoir is taken into account by defining the temperature of the solid zone as a linear function of temperature, which represents the variation in thermal properties across different geological layers. This temperature distribution is critical for simulating the natural heat transfer processes within the reservoir.
Dr. Carley Davis –
I’m truly amazed by how the geothermal reservoir simulation enhances our understanding of heat transfer processes underground. The detail about the vortex at the bottom of the U-tube contributes significantly to the efficiency of the heat exchange, and it’s fascinating how natural convection plays a crucial role in this. Thank you, MR CFD Company, for such an insightful product!
MR CFD Support –
Thank you for your kind words! We are thrilled to hear that our simulation of a geothermal reservoir helped deepen your understanding of geothermal heat transfer and natural convection. At MR CFD, we strive to provide detailed and accurate simulations to aid in learning and development. Your feedback is much appreciated!
Damion Strosin –
Fantastic tutorial! Learning about geothermal reservoir simulation with a DHE system was extremely helpful, and the step-by-step explanation of the methodology was clear and easy to follow. It was intriguing to see the temperature gradients and fluid flow represented in the simulation results.
MR CFD Support –
Thank you for your thoughtful review! We are delighted to hear the tutorial was helpful and that the simulation results provided clarity on the temperature and fluid flow aspects of geothermal reservoirs. Your positive feedback is greatly appreciated!
Mr. Sigrid Kshlerin III –
The simulation results are fascinating! Could you explain how gravity affects the simulation and the heat transfer in a bit more detail?
MR CFD Support –
Sure! In geothermal reservoir simulations like this one, gravity plays a critical role as it drives natural convection currents within the fluids. The water in contact with the hotter parts of the reservoir becomes less dense and rises due to gravity. As it rises, it transfers heat to the fluid in the tube, warming it up. The now cooler, denser fluid sinks, creating a circulation pattern that continues to move heat from the reservoir to the water in the U-tube. This convection process is essential for efficient heat extraction in geothermal systems.
Jason Ryan –
I’m really impressed by the detail in your geothermal reservoir simulation. Could you please tell me more about how the linear temperature gradient in the solid zone influences the overall efficiency of the heat extraction process? Thank you for sharing such fascinating results!
MR CFD Support –
Thank you for your compliment on our geothermal reservoir simulation! The linear temperature gradient in the solid zone is a crucial factor for mimicking the natural geothermal gradient found in geological formations. This setup allows the simulation of increasing temperature with depth, which is essential for understanding the efficiency of heat extraction. In our model, the temperature changes establish a convection-driven process inside the U-tube and the borehole. It causes cooler water at the top of the reservoir to sink and absorb heat as it flows downward. Consecutively, the heated water rises and transfers the heat to the working fluid inside the U-tube. The simulation results showed an increase in the outlet temperature of the tube water, indicating successful heat extraction facilitated by the established temperature gradient. The constant temperature change establishes ongoing natural convection that maximizes the heat transferred from the reservoir to the water in the U-tube, leading to efficient geothermal energy utilization.
Clark Rohan –
I found your tutorial on the geothermal reservoir simulation very insightful! I’m curious, how are velocity vectors able to indicate the level of turbulence inside the hole, and why does this affect the heat transfer process?
MR CFD Support –
In the simulation, velocity vectors are used to visually represent the flow direction and magnitude of fluid within the borehole. When these vectors curve and twist in complex patterns, it can indicate turbulent flow. Turbulence enhances mixing and disrupts the thermal boundary layer, leading to better heat transfer between the geothermal reservoir and the working fluid in the U-tube. Hence, increased turbulence usually results in more effective convective heat transfer as observed in the simulation.
Barney Senger –
I am thoroughly impressed by the detailed application of the realizable k-epsilon turbulence model in this simulation, the gravity consideration for convection, and the temperature-dependent properties. The explanation of natural convection within the geothermal reservoir was also particularly insightful. The heat transfer success is evident in the outlet temperature you’ve reported. Fantastic work!
MR CFD Support –
Thank you so much for your kind review! We’re thrilled to hear you found the detailed application of the turbulence model and the gravity effects enlightening. Our team strives to create detailed and practical simulations to truly capture the dynamics of such systems. We’re glad that the explanation of the natural convection process and the simulation results met your expectations and provided you with the insight you were looking for. Your positive feedback is a huge encouragement to us!
Mr. Eduardo Kerluke –
The U-tube in this geothermal reservoir simulation is quite fascinating. The increase in outlet temperature suggests efficient heat transfer, but I wonder how the natural convection is initiated within the borehole. Could you explain what starts the convective flow and why it forms a vortex at the bottom?
MR CFD Support –
The natural convection in the borehole is initiated by the temperature gradient due to the geothermal heat from the ground. As the working fluid at the bottom of the U-tube absorbs heat, it becomes less dense and rises. This rising fluid is replaced by cooler, denser fluid moving down, creating a convective flow. The vortex forms at the bottom part of the hole due to the buoyant forces acting on the heated fluid combined with geometrical constraints of the borehole, creating a rotational flow.