Non Newtonian Blood Pulse Flow in a Vein, ANSYS Fluent CFD Training
$180.00 Student Discount
- The problem numerically simulates Non-Newtonian Blood Pulse Flow in a Vein using ANSYS Fluent software.
- We design the 3-D model by the Design Modeler software.
- We Mesh the model by ANSYS Meshing software, and the element number equals 397388.
- We perform this simulation as unsteady (Transient).
- We use a UDF to define the pulse of the blood flow.
- The Carreau Equation is used for viscosity definition to consider non-newtonian blood.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Description
This simulation is about non-newtonian blood pulse flow in a vein via ANSYS Fluent software. We perform this CFD project and investigate it by CFD analysis.
The fluid used in this simulation is blood, a non-Newtonian fluid. Non-Newtonian fluids are fluids whose viscosity varies with their reaction rate, meaning they lack a specific viscosity.
In this type of fluid, the relationship between the shear stress variations and the applied stress rates is nonlinear; therefore, there is no constant coefficient of fit for viscosity. We do this transient simulation for 0.5 s. By the way, we apply a User-Defined Function (UDF) to model the pulse of the blood flow.
Since blood flow doesn’t have constant velocity and pulsed, the velocity function must be used periodically using the User-Defined Function code.
The geometry of the present model is drawn by Gambit software. The present model consists of a cylindrical vessel and two smaller vessels with a smaller size and diameter, such that one branch has a 90-degree angle and the other, a branch with a 45-degree curvature.
The present model consists of one input section and two output sections.
The model is then meshed by ANSYS Meshing software. The model mesh is unstructured, and 397388 cells have been created.
Non Newtonian Blood Method
Since the fluid used in this simulation is blood at a density of 1050 kg/m3 and blood is a Non-Newtonian fluid type, the Carreau equation with certain parameters has been used.
Newtonian fluids generally have constant viscosity during force application, but non-Newtonian fluids have variable viscosity during force application, which has different types.
Time-dependent non-Newtonian fluids have two categories: Rheopectic, such as printer ink and cream, which increase their viscosity over time, and Thixotropic, such as honey, whose viscosity decrease when the force is applied.
Time-independent non-Newtonian fluids are also divided into three groups: Dilatants such as starch and clay, whose viscosity depends only on the force value applied, and Pseudoplastic, such as greases, paints, soaps, and ketchup, which are inversely correlated with the force value applied.
Other groups called Bingham, such as toothpaste and silica nanocomposites, have a stress threshold or a certain amount of force and tension to flow. In the present simulation, blood is used as a Pseudoplasticity non-Newtonian fluid defined by the Carreau model.
This model attempts to create a wide range of fluids by establishing a curve commensurate with the Newtonian and non-Newtonian fluid functions of the type of subtractive stress (Pseudoplasticity).
Non Newtonian Blood Conclusion
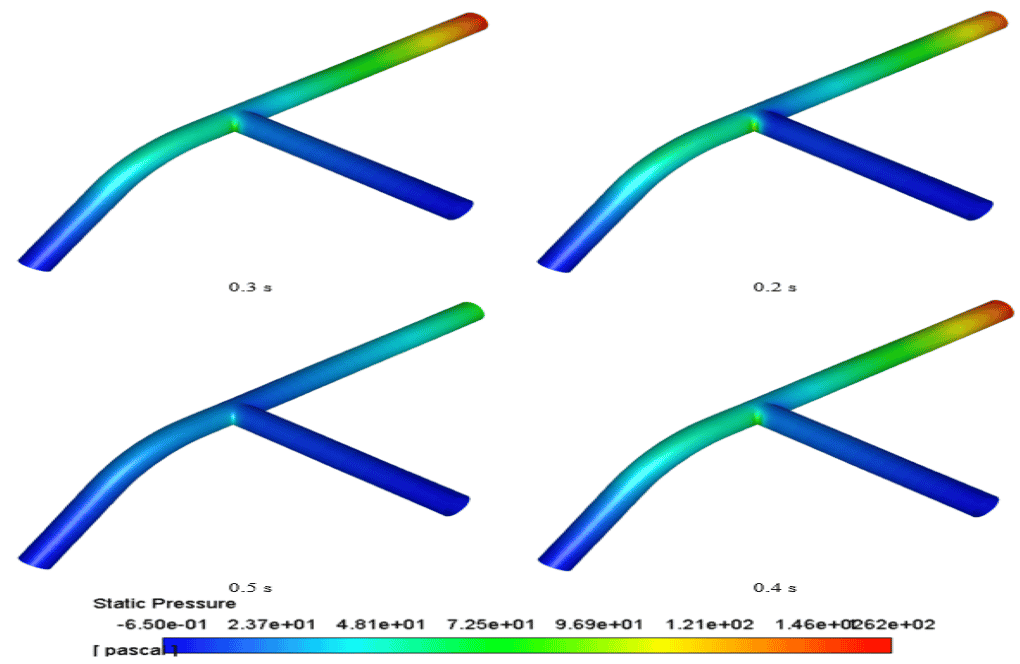
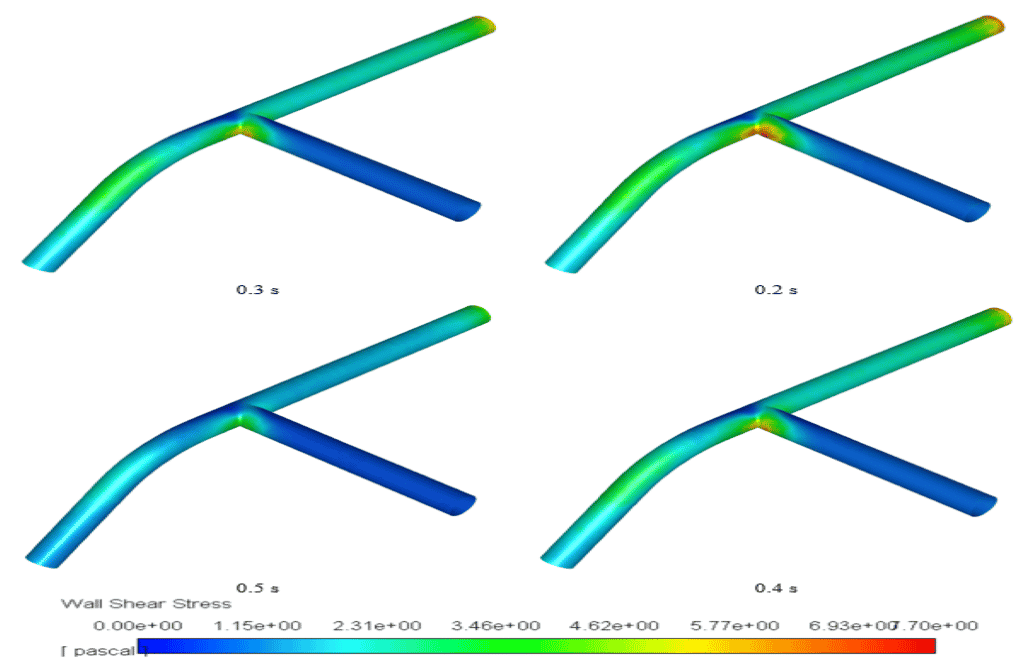
After simulation, the contours of pressure and wall shear stress are obtained at different times. The results show that the flow inside the vessel is completely pulsatile; Because the pressure changes at different times.
Also, the results show that the pressure corresponds to the wall shear stress. An increase in pressure inside the vessel leads to an increase in the wall shear stress.





Ms. Savanna Rippin –
What boundary conditions are used in the Non-Newtonian Blood Flow in the Vein CFD Simulation?
MR CFD Support –
We use pressure boundary conditions at the inlet and outlet of the vein. These conditions are based on typical physiological pressures.
Emile Reinger –
I am thrilled with how well the Carreau model mimicked the real blood properties in this simulation. The pulsatile nature of the blood flow due to the UDF code was fascinating to observe. However, I am curious about whether Platlet-Rich Plasma (PRP) treatments would affect these simulations’ outcomes or whether different modeling approaches are needed.
MR CFD Support –
Thank you for your positive feedback on our Non-Newtonian Blood Pulse Flow CFD Simulation. Concerning your question, Platelet-Rich Plasma (PRP) treatments change the composition of the blood, potentially altering its rheological properties resulting in differing viscosity or other characteristics influencing flow behavior. These changes may require adaptation to the simulation, whether through modified parameters in the Carreau model or the employment of a different non-Newtonian model. The specifics of how PRP affects rheology would dictate the required adjustments or if a new approach is warranted.
yacine –
i need to dowland this project and i hve a question
i need to activate FSI structural analyse for this project and i have not the materiel of my géometrie haw a can selected the material and proprities of material
Gerson Steuber –
The learning material provided a comprehensive overview of blood flow modeling. Did it also include guidance on creating and implementing the UDF for blood pulsation?
MR CFD Support –
The learning material includes examples and step-by-step instructions on how to create a User-Defined Function (UDF) to model the pulsating flow of blood, along with tips on how to implement and debug it within the ANSYS Fluent environment.
Catalina Luettgen –
I really appreciated how MR CFD explained the complex concept of non-Newtonian fluid behavior, and the application of the Carreau model for blood flow simulation was insightful. The User-Defined Function usage made the pulse flow simulation quite realistic. Great job!
MR CFD Support –
Thank you for your positive feedback! We’re delighted that our training helped clarify the intricacies of non-Newtonian fluid behavior and provided valuable insight into blood flow simulation using the Carreau model. Your satisfaction with the application of UDF for pulse flow modeling means a lot to us. If there’s anything else we can assist you with, please do not hesitate to ask.
Bertram Langworth –
How do you model the non-Newtonian behavior of blood in this simulation?
MR CFD Support –
We use the Carreau-Yasuda model in ANSYS Fluent to simulate the non-Newtonian behavior of blood. This model accurately represents the shear-thinning property of blood.
Merritt Witting –
The simulation quality for the Non Newtonian Blood Pulse Flow in a Vein seems intense and precise. I appreciate how the pulsatile nature of blood flow is captured and represented, particularly how blood’s non-Newtonian properties are addressed using the Carreau model. Well done!
MR CFD Support –
Thank you for your kind words! We strive for accuracy and precision in our simulations and are glad to see that the effort put into capturing the complex nature of blood flow in the Non Newtonian Blood Pulse Flow simulation has been appreciated. Your feedback is very valuable to us.
Gregorio Champlin IV –
What kind of reviews would be appropriate for concepts covered in the description?
MR CFD Support –
It seems there may be some confusion in your request. You provided a description about a CFD simulation training product focusing on non-Newtonian blood pulse flow in a vein. An appropriate review could include comments on the complexity of the physics covered, the effectiveness of the UDF in modeling pulsatile flow, or the clarity in application of the Carreau model for the non-Newtonian blood fluid. Also, how well does the product guide through the understanding and interpretation of simulation results such as wall shear stress and pressure distributions over time should also be potential aspects for a review.
Ruthe Kozey –
The Non-Newtonian Blood Flow in the Vein CFD Simulation is incredibly accurate and detailed. Great job!
MR CFD Support –
Thank you for your kind words! We strive to provide accurate and detailed simulations to our customers.
Nicklaus Kerluke I –
The review thoroughly explains the simulation process and objectives. Excellent work!
MR CFD Support –
Thank you for your positive feedback on our training for the non-Newtonian blood pulse flow simulation in a vein. We’re thrilled to hear that you found the explanation clear and the process well-defined. Your satisfaction is our top priority!