Coronavirus Dispersion in an Elevator due to Sneeze
$160.00 Student Discount
- The problem numerically simulates the Corona virus Dispersion in an Elevator Cabin due to a Sneeze using ANSYS Fluent software.
- We design the 3-D model with the Design Modeler software.
- We mesh the model with ANSYS Meshing software, and the element number equals 454433.
- We use the Species Transport model to define evaporating species.
- We use the Discrete Phase Model (DPM) to define droplet particles.
Click on Add To Cart and obtain the Geometry file, Mesh file, and a Comprehensive ANSYS Fluent Training Video.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Coronavirus Dispersion in an Elevator Cabin Due to a Sneeze, CFD Simulation by ANSYS Fluent
The coronavirus (COVID-19) is currently recognized as the greatest human challenge in the world; Because this disease, in addition to being dangerous to human health, has a high transmission power between sick people and healthy people.
Coughing or sneezing of a sick person without a mask in space causes the spread of coronaviruses. One of the important recommendations of physicians in preventing the transmission of disease between people is to care about the social distance between people in society.
The elevator cabin is one of the most important spaces in the discussion of coronavirus disease; Because usually a number of people with the shortest possible distance are placed in a small space with a not very strong ventilation system.
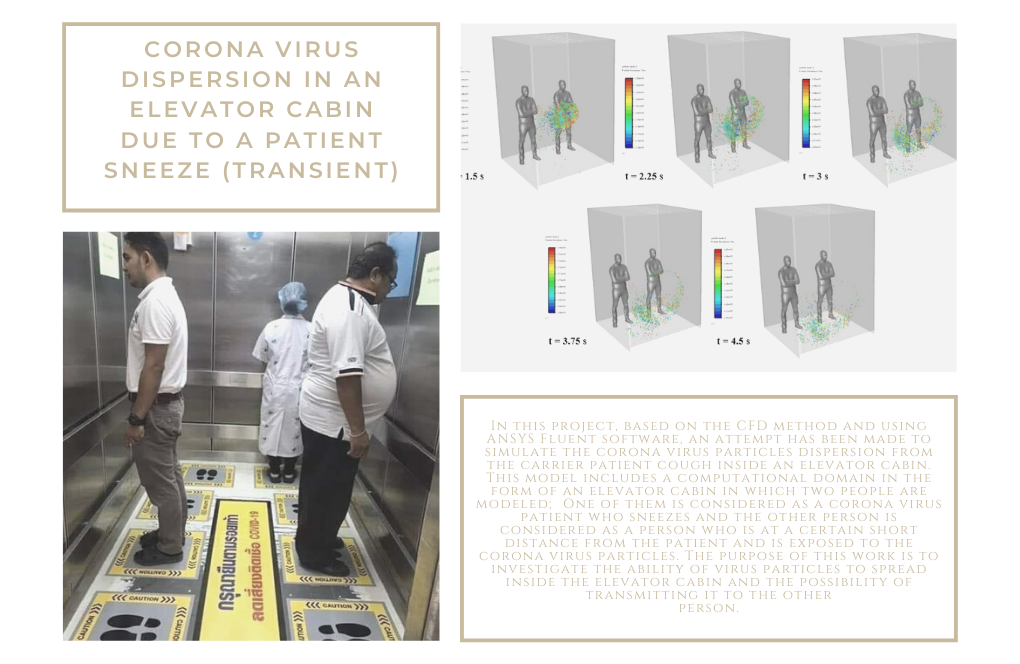
In this project, based on the CFD method and using ANSYS Fluent software, an attempt has been made to simulate the coronavirus particles dispersion from the carrier patient cough inside an elevator cabin.
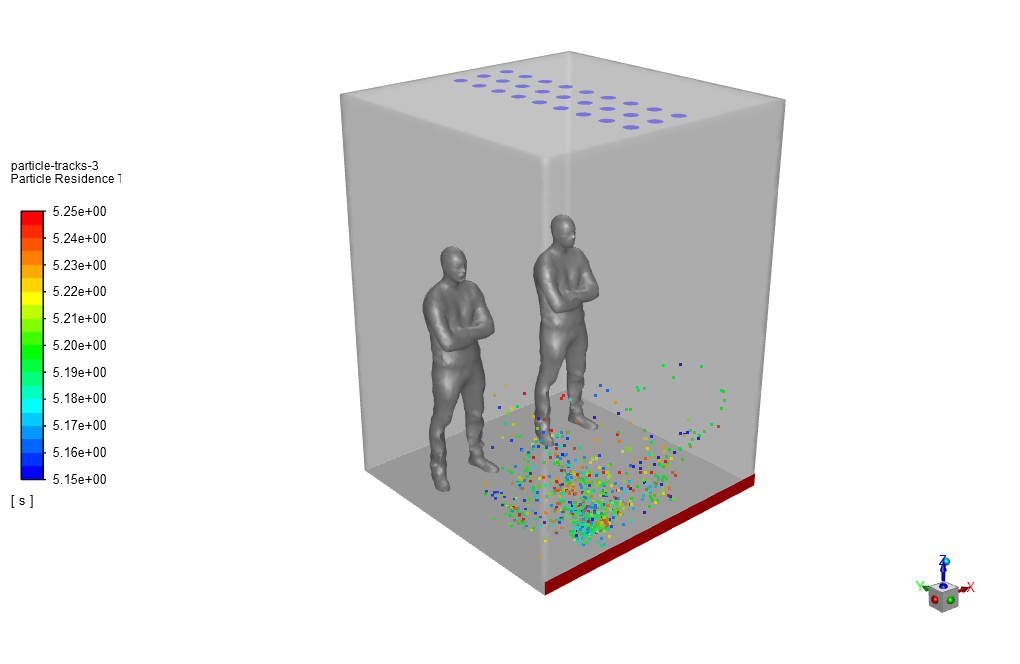
This model includes a computational domain in the form of an elevator cabin in which two humans are modeled; One of them is considered a coronavirus patient who coughs or sneezes and the other person is considered a person who is at a certain distance from the patient and is exposed to the coronavirus particles.
The purpose of this work is to investigate the ability of virus particles to spread inside the elevator interior and the possibility of transmitting it to another person.
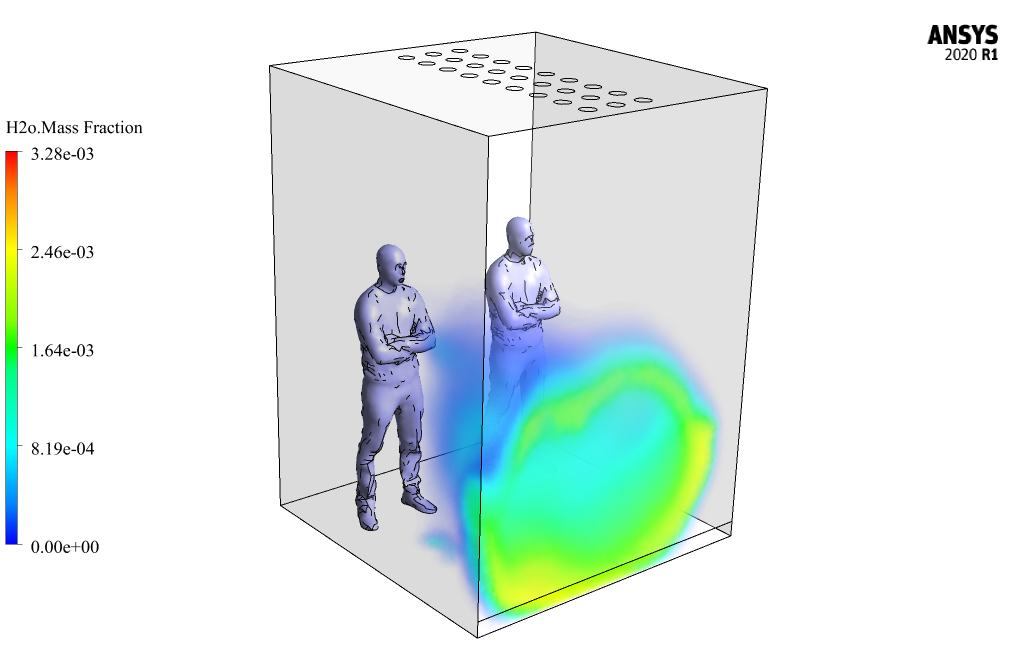
According to this definition of injection, human cough virus particles are physically expelled from the patient’s mouth by water droplets that are evaporating in space.
These virus droplets have a temperature of 310 K, a velocity of 31.85 m/s, and a mass flow of 0.018 kg/s, which are emitted at intervals of 0s to 0.1s.
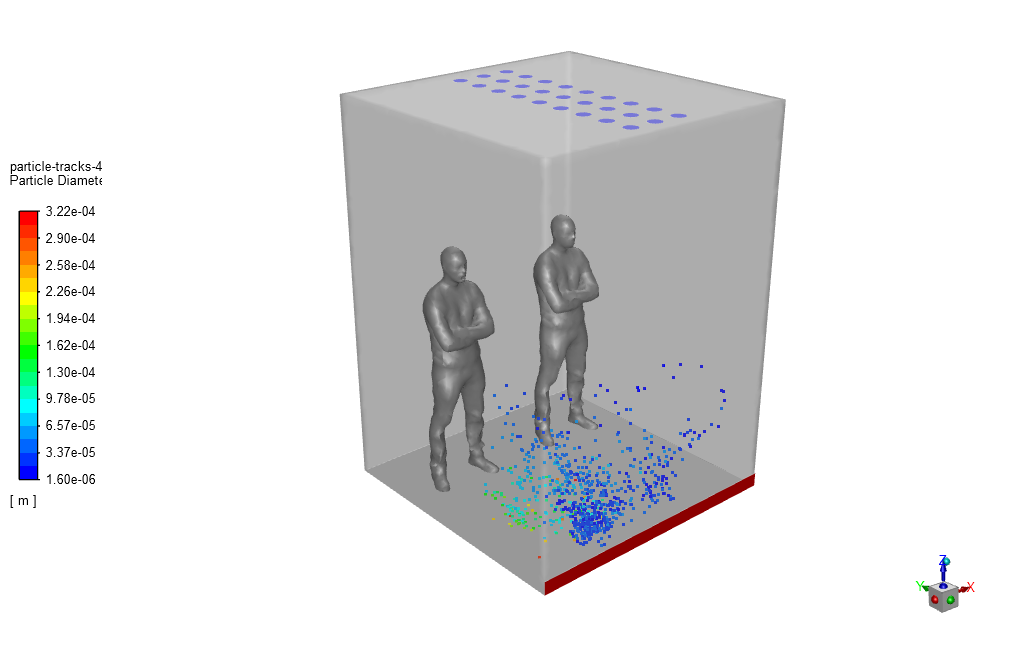
The particle diameter of the virus is not constant during propagation and the rosin-rammler-logamethric distribution method is considered for the size of the diameters.
The present model is designed in three dimensions using SOLIDWORKS and Design Modeler software. Also, we carried out the meshing of the model using ANSYS Meshing software and the mesh type is unstructured. The element number is 454433.
CFD Methodology
For the present simulation, the discrete phase model (DPM) is used; Because this model allows us to study a mass of particles discretely in a continuous fluid space.
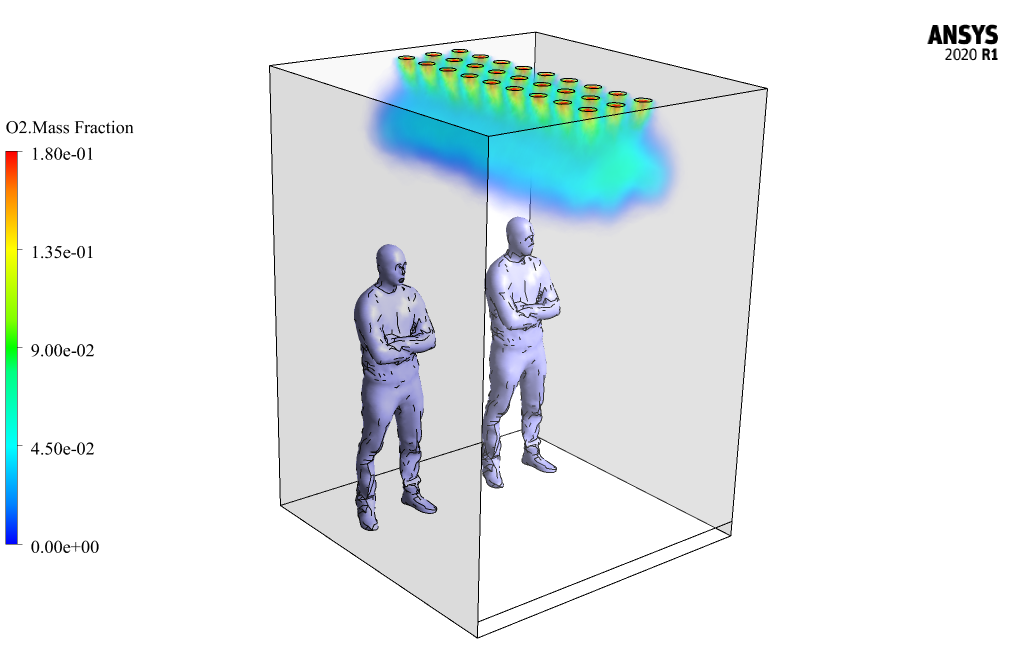
Due to the choice of this model, the wet particles of the coronavirus secreted from the patient’s mouth are considered a discrete phase and the airflow transmitted through the elevator ventilation valves is considered a continuous phase inside the interior of the elevator cabin.
The physical models of discrete particles defined in this simulation include two-way turbulence coupling meaning the two-way interaction between continuous and discrete phase (in addition to the discrete phase being affected by the continuous phase, by activating the interaction with continuous phase mode, the discrete phase also affects the continuous phase), stochastic collision means irregular droplets collide with each other, coalescence means droplets merge with each other, and breakup means The collapse of the droplets.
Following this method and the relevant formulation, the values related to the minimum, maximum and average diameter size determine the exponential parameter of the spread and the number of diameters per injection.
It should be noted that the drop mode is applied when the species transport model is also activated. In addition, the energy equation is activated to consider the temperature changes.
Coronavirus Dispersion in an Elevator Conclusion
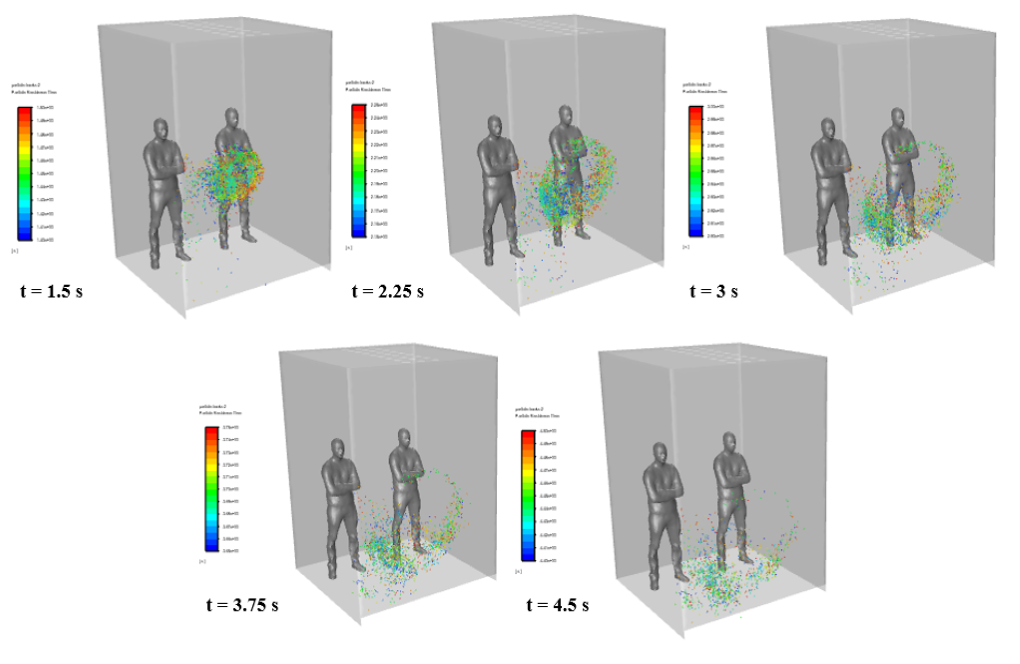
At the end of the solution process, we obtain the virus particle tracking at the last second of the simulation process. This particle tracking is based on residence time and particle diameter size.
We also export the animation of the virus dispersion and its disappearance over time and attached it to the project report file. Finally, we obtain three-dimensional contours related to the temperature and mass fraction of oxygen released from the ventilation system and water droplets secreted from the cough.

Ms. Jany Heller –
I am impressed by the extent of this study! Could you please explain how the coronavirus particle dispersion animation helps in understanding the spread in an elevator?
MR CFD Support –
Thank you for your kind words! The animation of coronavirus particle dispersion is a vital visualization tool that helps observers to comprehend the dynamics of how virus particles spread over time within the enclosed space of an elevator. It illustrates the travel pathway, concentration, and areas of risk as the particles move around in the air. This allows for a better understanding of potential exposure and reinforces the importance of mitigation strategies like ventilation and social distancing.
Prof. Karolann Armstrong MD –
Can this model simulate different coughing or sneezing scenarios, such as varying the droplet sizes or the number of people in the elevator?
MR CFD Support –
Yes, this model can simulate a range of scenarios by adjusting the input parameters like droplet sizes using the rosin-rammler-logamethric distribution method and by modifying the number of people and their positions within the elevator cabin in the simulation setup.
Verlie Schuppe –
The description of the product is clear and educational – learning how the virus disperses in enclosed spaces like an elevator can be key for designing better ventilation systems. The use of ANSYS Fluent in simulating such a scenario is impressive, as it combines the reality of COVID-19’s transmission through aerosols with complex computational fluid dynamics principles. This kind of study could have major implications for public health and safety.
MR CFD Support –
Thank you so much for your kind review! We’re pleased to hear that you found the project educational and applicable to real-world situations. Your insight into the importance of CFD in public health is valued and we aim to provide simulations that can help design better ventilatory precautions in these critical times.
Alexa Leannon –
Very informative and top-notch simulation process! Seeing the particle dispersion was enlightening. It will undoubtedly help with designing better ventilation systems for public spaces like elevators.
MR CFD Support –
Thank you for your positive feedback! We’re delighted to hear that the simulation provided valuable insights into airflow and pathogen dispersion. It is our goal at MR CFD to contribute to the safer design of public areas. If you have any further questions or require more detailed insights, please feel free to reach out.
Dr. Osborne Dickinson –
It was interesting to read about how the dispersion of coronavirus particles is affected by sneezing in an enclosed elevator. Keep up the good work on such relevant and thought-provoking simulations.
MR CFD Support –
Thank you for your positive feedback! We’re glad you found the simulation both interesting and insightful. We believe it’s crucial to understand the dynamics of virus particle dispersion in everyday scenarios so that we can better protect ourselves. Stay tuned for more informative and compelling studies.
Omari Bins –
What advancements could be implemented in future simulations to even more accurately predict virus dispersion in enclosed spaces?
MR CFD Support –
For future simulations aiming to increase accuracy in predicting virus dispersion in enclosed spaces like elevators, the following advancements can be considered: improving the complexity of airflow modeling to include directional air jets, boosting resolution to capture fine droplets, incorporating humidity and temperature variations over time, employing more sophisticated models for aerosol physics, extending particle interactions including viral survival rate based on environmental factors, and validating the CFD model with experimental data.
Darlene Weber –
Really impressive analysis. Your product helped immensely in understanding aerosol transmission dynamics for safety measures.
MR CFD Support –
Thank you very much for your kind words. We are delighted to hear that our CFD analysis could provide valuable insights into the safety measures for aerosol transmissions. Your safety and understanding are our priority!
Verla Wunsch –
This product does a great job in visualizing the dispersion of coronavirus particles. I was truly impressed by its detail!
MR CFD Support –
Thank you for your positive feedback! We are delighted to hear that you found our CFD simulation and visualization details impressive. Our team works hard to provide accurate and educative simulations, and we appreciate your recognition. If you have more feedback or need further information, please feel free to reach out.
Maye Cassin –
Excellent and timely study. The detailed mention of the air flow characteristics and particles interaction was especially informative. Really appreciated the use of the discrete phase model to track the virus particles accurately!
MR CFD Support –
Thank you for your positive feedback! We are delighted to hear that you found the study’s methodology using the discrete phase model and the detailed analysis informative. If you have any further questions or need more information regarding our simulations, feel free to ask. We’re committed to providing valuable and timely research to help tackle real-world challenges.
Prof. Dillon Miller –
The narration of the process flow and the theoretical premise of this coronavirus dispersion simulation is absolutely first-rate!
MR CFD Support –
Thank you for your positive feedback on our coronavirus dispersion simulation! We’re delighted to know that the explanation of the process and theory behind the simulation met your expectations and was informative. If there’s anything else we can help you with or if you’re interested in other simulations, please let us know!
Alex Berge –
The product was exceptional in showing how social distancing within confined spaces like an elevator is crucial during the COVID-19 pandemic. The detailed dispersion analysis paired with temperature and mass fraction data illustrated the rapid spread and potential risks associated with sneezing or coughing in such environments. Hats off to the MR CFD company for creating an insightful simulation that combines complex CFD methodologies with pertinent real-world applications.
MR CFD Support –
Thank you for the positive feedback on our Coronavirus Dispersion in an Elevator simulation. We are glad to hear that you found it both educational and practically relevant during these challenging times. Your appreciation motivates our team to continue delivering high-quality and insightful simulations. Stay tuned for more cutting-edge studies from MR CFD.
Fernando Rowe –
This CFD simulation was super insightful! I appreciated learning about the dynamics of coronavirus particle dispersion in an elevator due to a sneeze. It’s amazing how you could visualize particle tracking and temperature changes in such a confined space.
MR CFD Support –
Thank you for your kind words! We’re thrilled to hear that the simulation proved to be educational and offered valuable insights into the dispersion of coronavirus particles in confined spaces. Visualization is a powerful tool in comprehending complex fluid dynamics, and we are pleased that it enhanced your understanding.