Offshore Pipeline Considering Hydrodynamic Force, ANSYS Fluent CFD Simulation Training

Description

The present problem simulates seawater flow around offshore pipelines by ANSYS Fluent software. We perform this CFD project and investigate it by CFD analysis.

The wave motion of the seawater on the offshore pipelines creates drag and lift forces. Therefore, the location of these transmission offshore pipelines must be in optimal condition to withstand less hydrodynamic forces.

We design the present 2-D model using ICEM software. The present model consists of a rectangular space for seawater flow and a circular section as an offshore pipe.

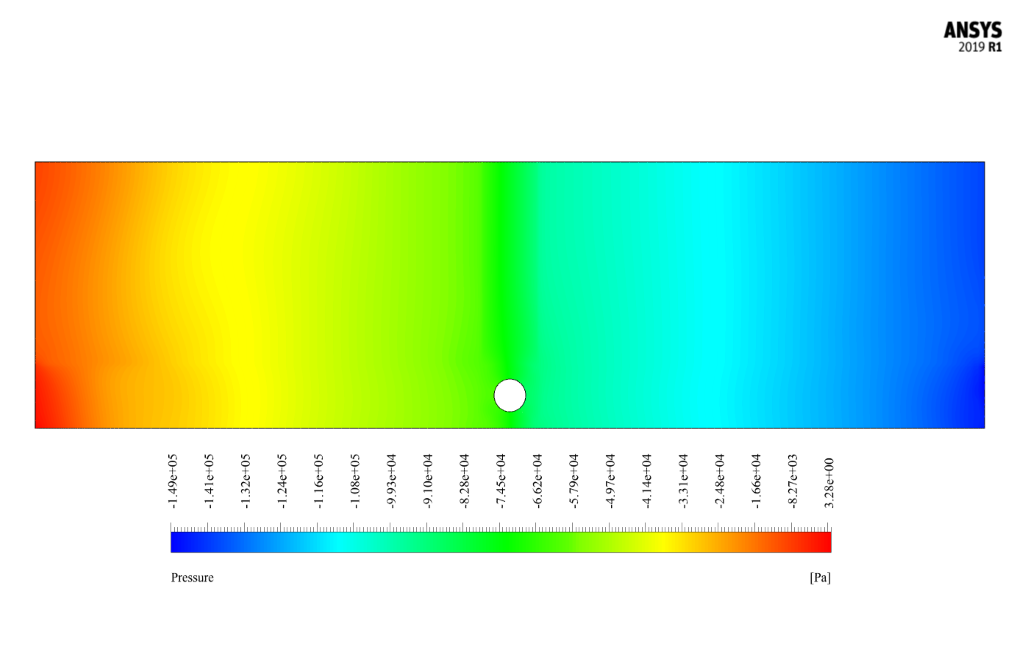
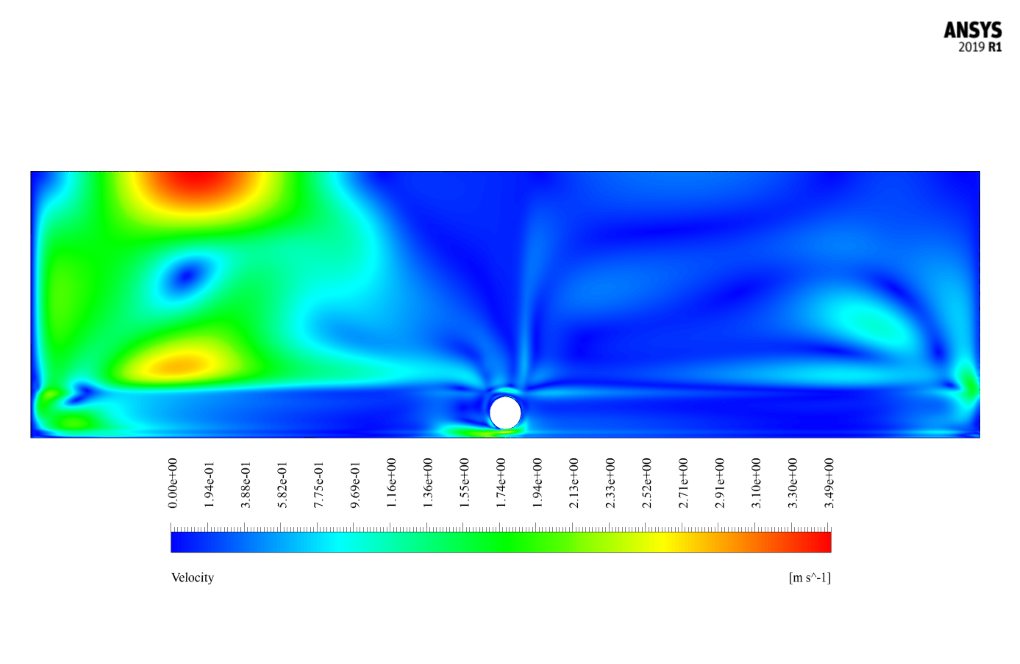
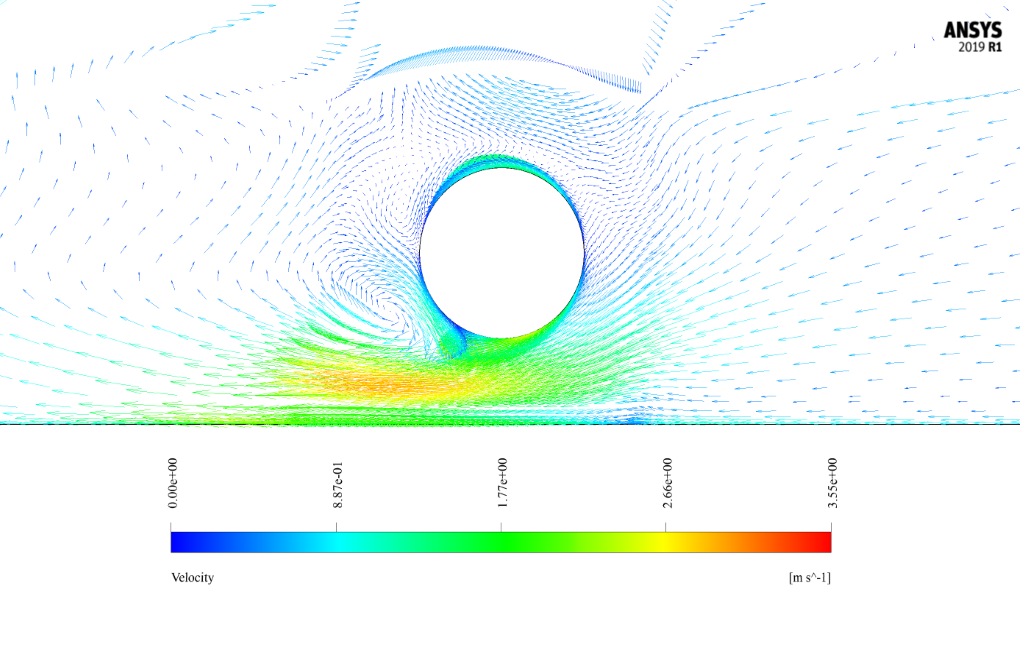
The two important longitudinal parameters in the model are the pipe diameter (D) and the distance between the bottom of the pipe and the seafloor (e), which is measured by the e/D ratio.

The diameter of the pipe has a constant value of 0.4 m. The value of e in the two different states is 0.2 m and 0.1 m. In addition, the length and height of the space for seawater are 12 m and 3.24 m, respectively.

We mesh the model using ICEM software, and the mesh type is structured. The element number is 135417. The cells adjacent to the circular section are smaller and more accurate.

In fact, the circumference of the circular section is divided into five different parts. We mesh in such a way that in the space close to the circle, the quality and accuracy of the mesh are higher.

Offshore Methodology

One of the geometric parameters measured in the present problem is the distance from the pipe floor to the seafloor ratio.

Given that the movement of seawater is wavy, it is necessary to define the input velocity as an equation of a wave flow using the UDF.

Also, the pressure inside the seawater is relative to the atmospheric pressure, and the pressure changes due to the wave motion of the seawater. So, we use the equation of the ambient pressure in the wave in the form of the UDF.

All functions related to the input velocity of the incoming water flow in the horizontal direction, the relative wave pressure, the turbulent kinetic energy, and the turbulence dissipation rate are all defined as the UDF in the software.

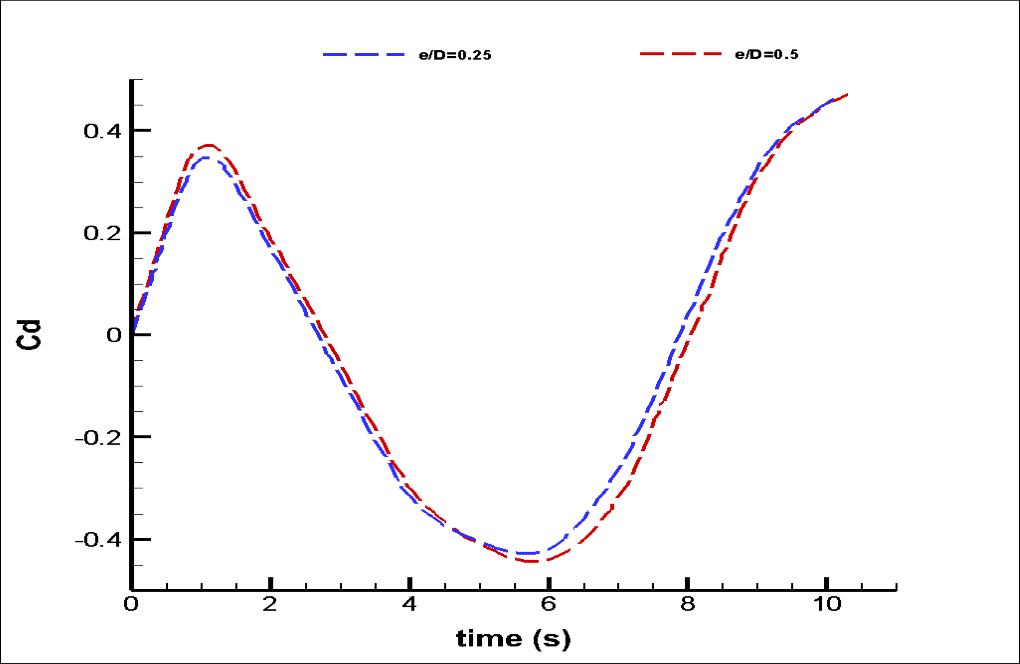
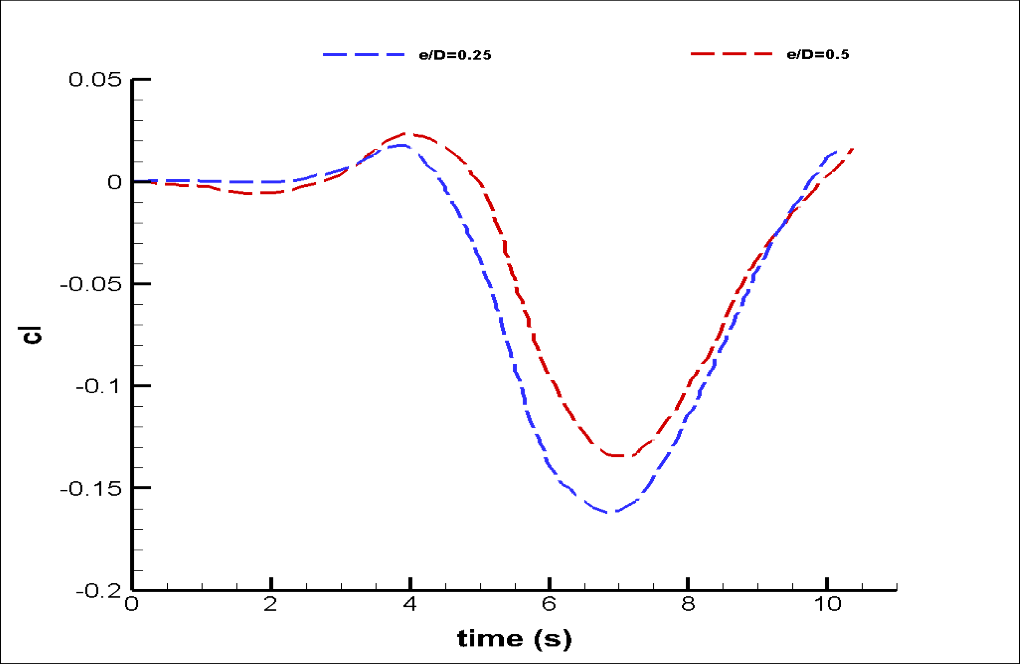
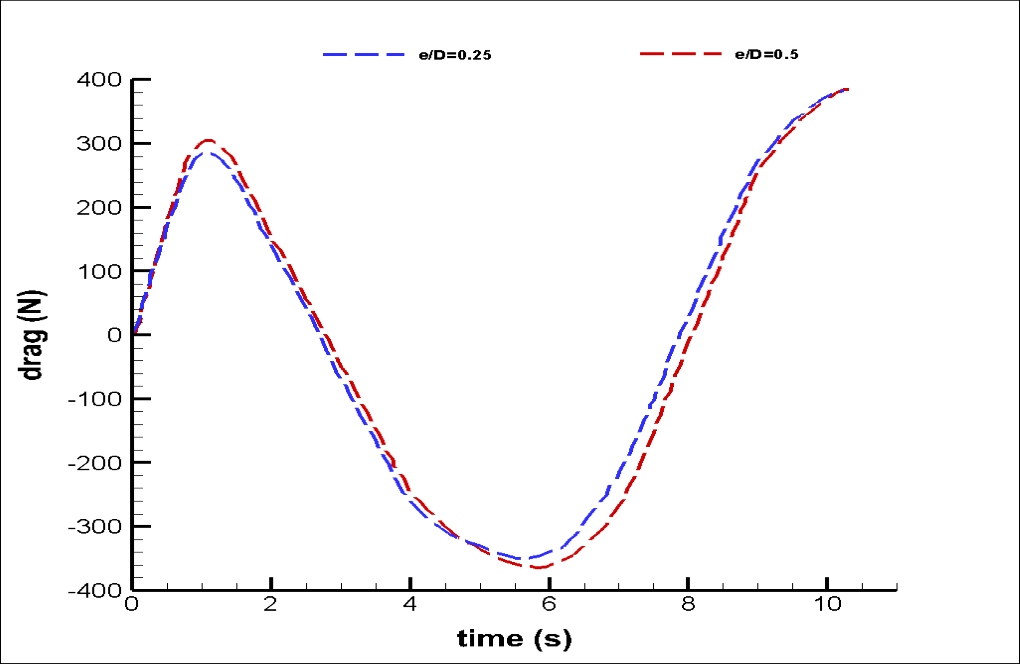
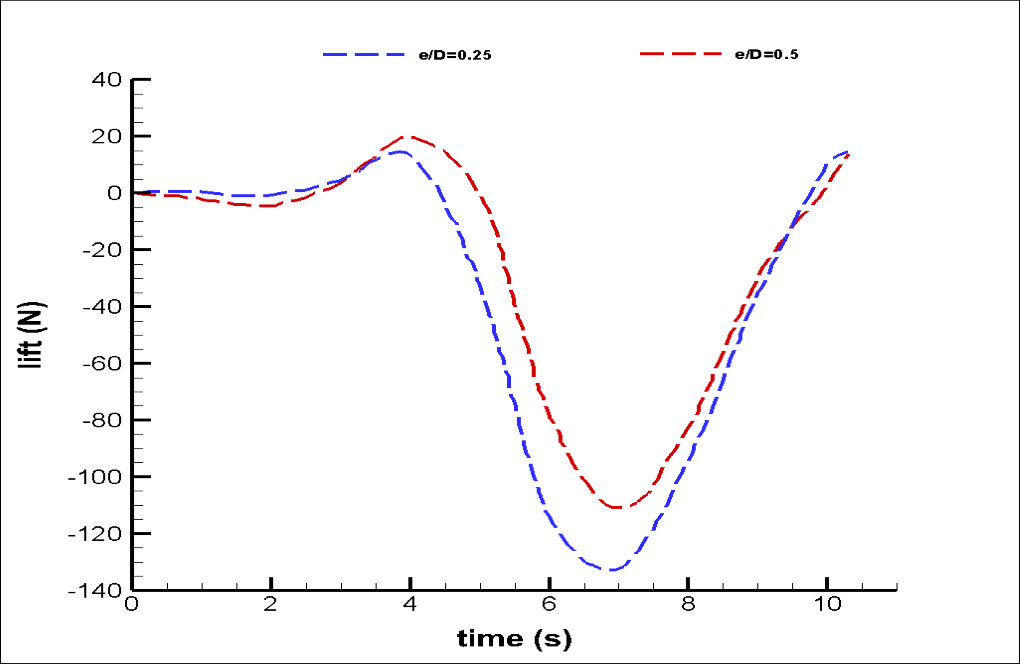
This project aims to compare the hydrodynamic forces on the pipeline over one period of the sea wave. We perform this process to achieve the optimal state.

In the present study, we consider the wavelength of seawater (the distance between the two peaks of the wave) to be 163.20 m, and the corresponding duration (period) is 10.3 s. Therefore, the dimensionless frequency number of the wave angle, i.e., 2π/Tw, is equal to 2π/10.3=0.61.

Also, we assume the maximum velocity at a wave peak to be 2,729 m/s. At the same time, km and Ԑm indicate the maximum turbulence kinetic energy and the maximum turbulence dissipation rate, respectively.

In the equation of the sea wave pressure, H is equal to the height of the sea wave. D is equal to the depth of the seawater. Also, -z is equal to the height of the water column. It’s in the point for which the dynamic pressure is calculated.

Also, d-(-z) is equal to the distance from the point for which the dynamic pressure is calculated to the bottom of the sea.

Offshore Conclusion

After the simulation, we obtain the two-dimensional velocity and pressure contours and the two-dimensional velocity vectors. These contours are related to two different modes (e/D=0.5 and e/D=0.25). These results are at the last second of the simulation process (10.3 s), i.e., at the end of a period of a complete alternation.

Also, we achieve graphs of changes in drag and lift hydrodynamic forces and drag and lift coefficients over time. These diagrams are also related to the two modes (e/D=0.5 and e/D=0.25).