Nanofluid Porous Mixer for Increasing Heat Transfer
$180.00 Student Discount
- The problem numerically simulates the Porous Mixer for Increasing the Heat Transfer of Nanofluid using ANSYS Fluent software.
- We design the 3-D model by the Spaceclaim software, and then mesh the model by ANSYS Meshing software.
- The Nanofluid is modeled as a single-phase fluid with modified thermophysical properties.
- We use the Porous option in the cell zone conditions.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Nanofluid Porous Mixer for Increasing the Heat Transfer, ANSYS Fluent CFD Simulation Training
In this project, mixing hot (303k) and cold (293) nanofluid flows were investigated while mixing these two streams once using 28 mixers and once using 54 mixers modeled as a porous medium.
Geometries were drawn in Spaceclaim software, and their meshes were generated by Ansys Meshing software. Two types of geometry are considered for this project. The first case is where there are 2 rows of mixers, and the second case is where there are 4 rows of mixers.
The grids created on the geometries are unstructured with the triangles method. The number of cells for case 1 is 87501, and for case 2 is 83180. There are two inlets to this project. Both have a velocity of 0.1 meters per second. But the temperature is 293 K for the upper and 303 K for the lower inlet.
Porous Mixer Methodology
A coupled algorithm was applied in the pressure-velocity coupling, and a model (Realizable-Standard) was chosen as a turbulence model. Nanofluid is modeled as a single-phase fluid with modified thermophysical properties. These properties are calculated using the formulas below. Mixers are simulated as porous mediums of aluminum with porous permeability equal to 1.
Where are the density, viscosity, specific heat, and thermal conductivity coefficient of nanofluid and the volume fraction of nanoparticles in the fluid.
We define the porosity number as follows:
Where Vv is the void volume and Vt is the total volume. According to the dimensions of the problem, the porosity is 0.937 for the 2-row case and 0.875 for the 4-row case.
Porous Mixer Conclusion
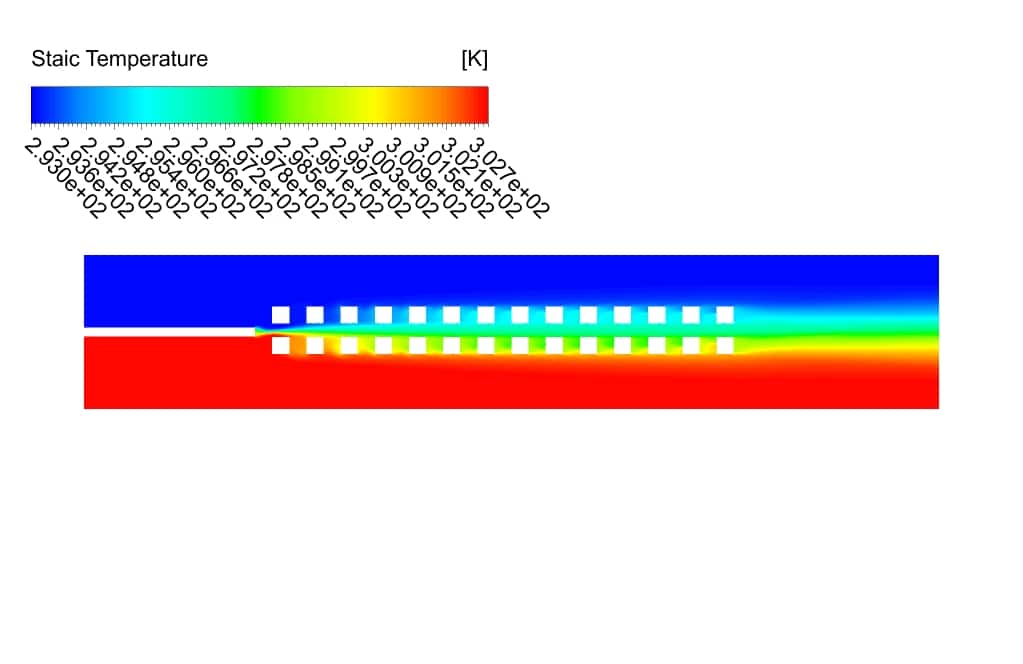
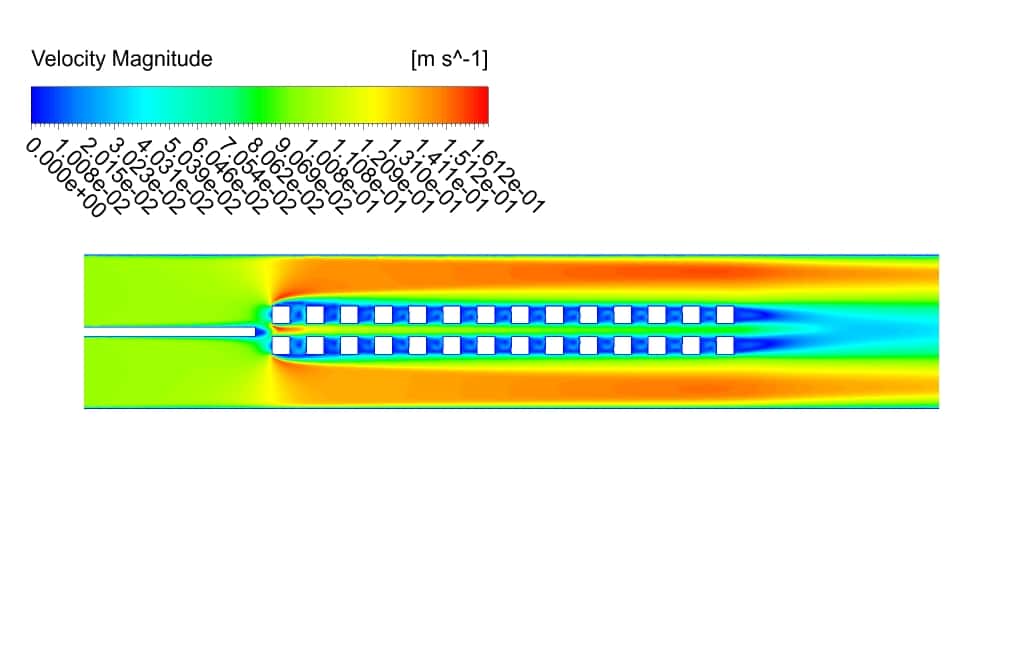
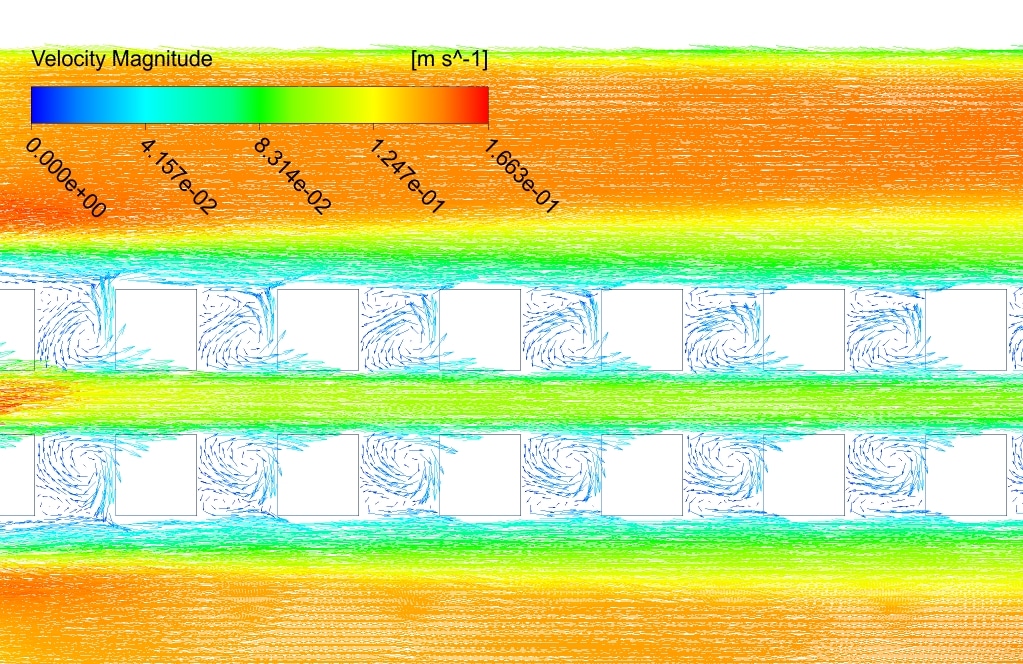
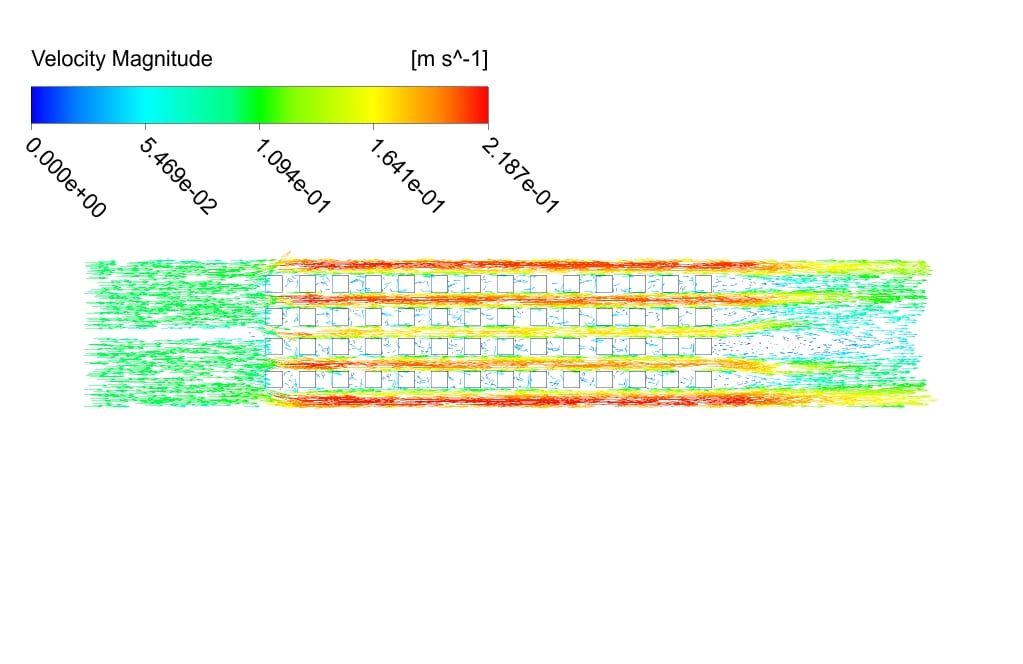
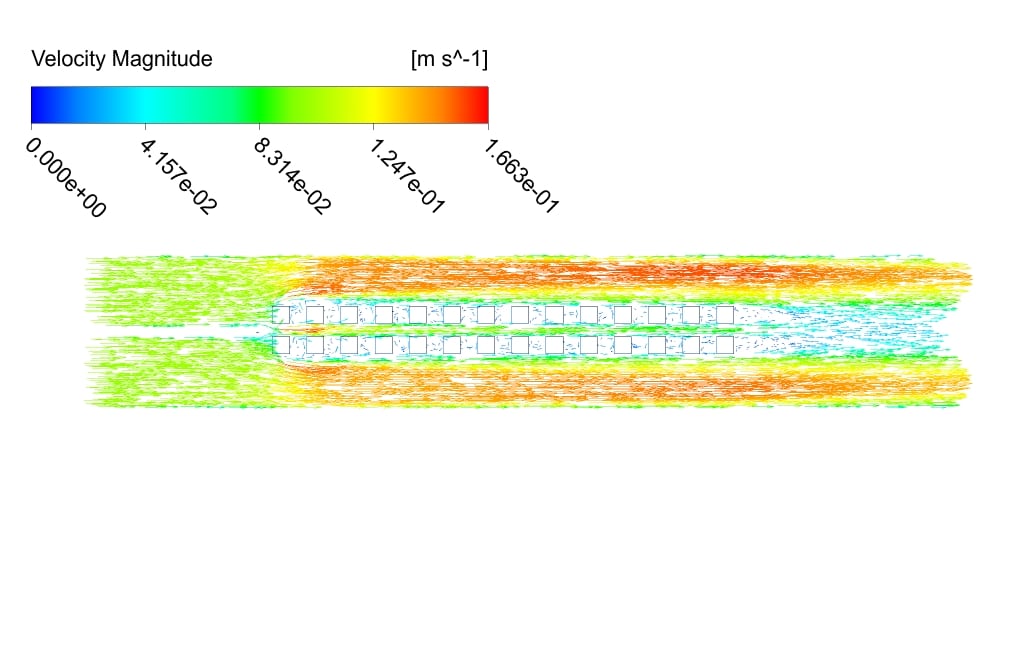
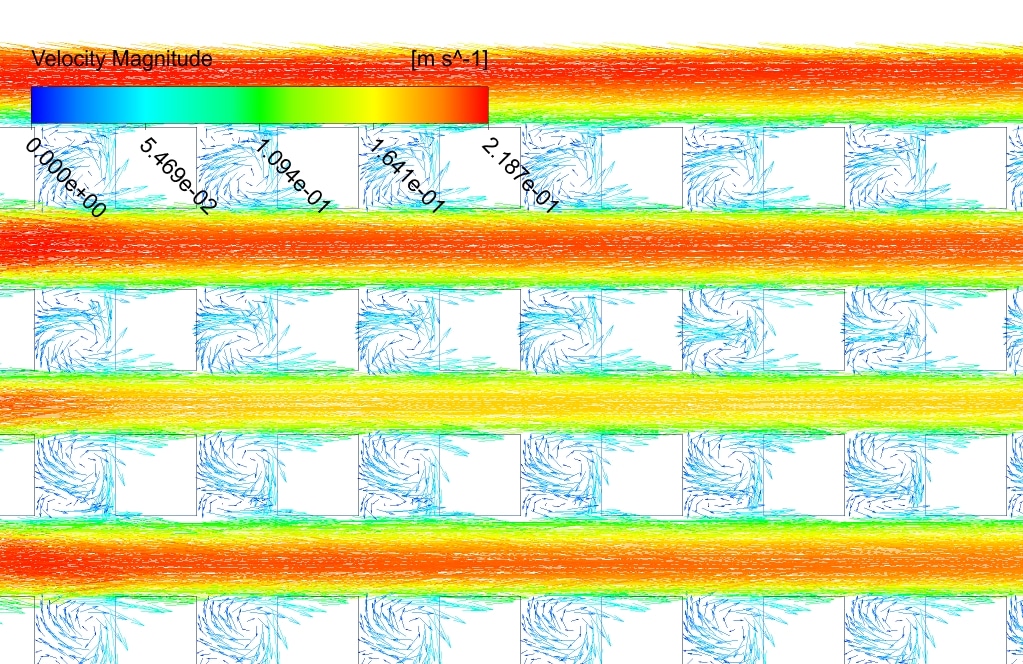
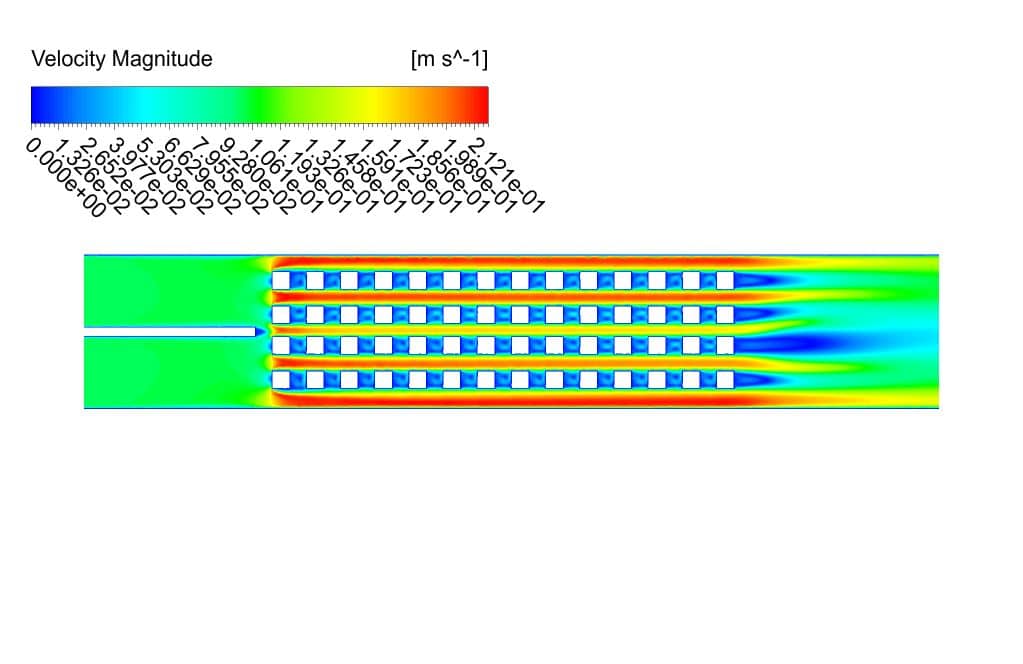
The velocity, static pressure, temperature contours, and vectors are obtained. As you can see from the pictures, the velocity contour is more uniform for the 2-row case.
The reason can be attributed to the smaller number of cubes and, as a result, less change in velocity gradient (due to the collision of the flow with the sharp edges). The maximum and average speeds are higher in the 4-row case.
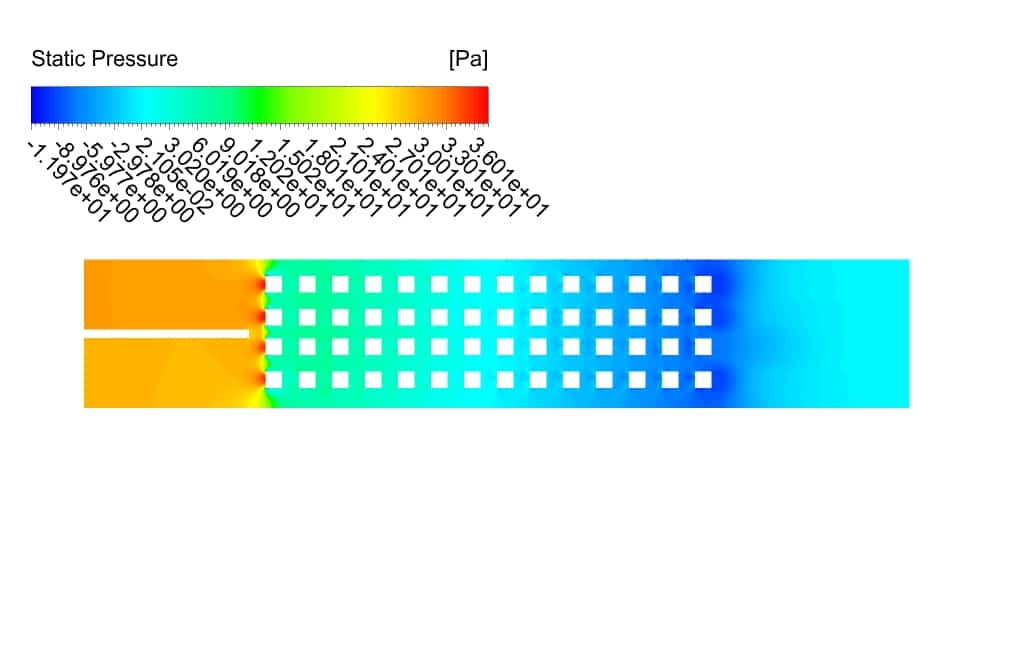
This indicates that although the number of separation zones is higher in the 4-row case, the separations are more substantial in the 2-row case. The pressure gauges also show that the pressure is more negative for the 2-row case. This is also understandable from Bernoulli’s equation.
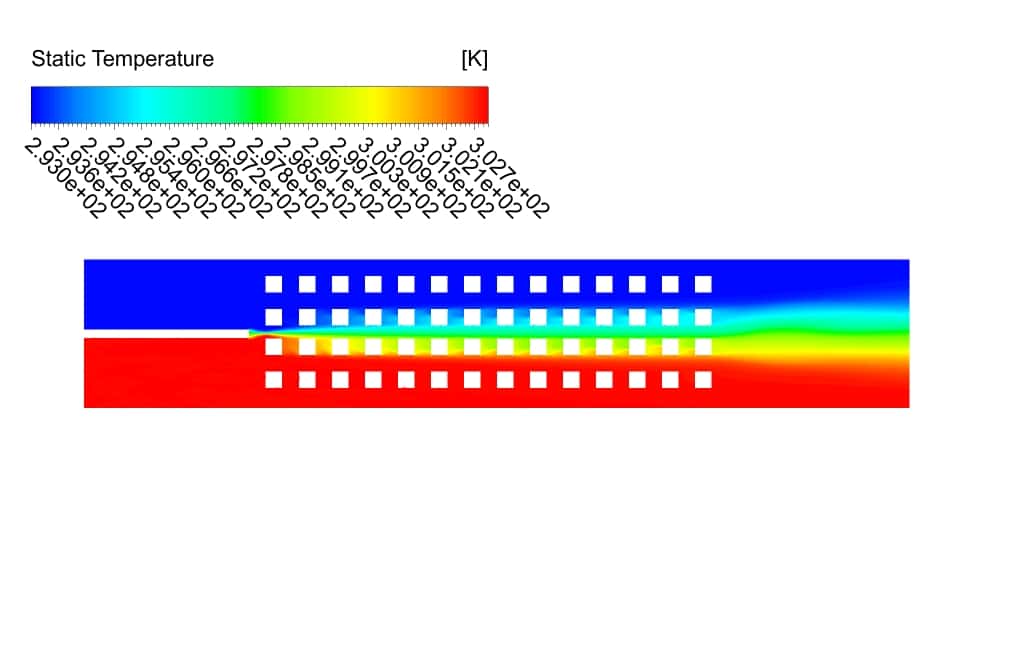
The pressure has more positive values at the top of the domain, where the temperature is lower than other temperatures on the domain. Temperature counters show that the maximum and average temperature values are the same for both cases.
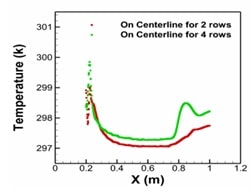
However, in the 4-row case, due to the shape of the geometry, the range of temperature changes is wider, and the changes are slower. We present the temperature diagram on the centerline of the geometries.
As we can see from the diagram, for the 4-row case, the temperature has a higher value in the center of the geometry due to the more significant number of separation zones.


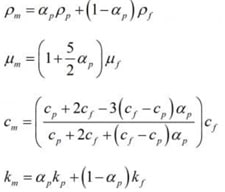
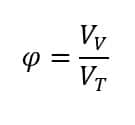


Dr. Esmeralda Gutkowski –
Can this simulation handle non-Newtonian fluids?
MR CFD Support –
The current model is set up for Newtonian fluids, but we can modify the simulation to handle non-Newtonian fluids upon request.
Shanon Buckridge –
Can this simulation be used for academic research?
MR CFD Support –
Absolutely. Our simulations can be a valuable tool for academic research in fields such as heat transfer and fluid dynamics.
Jasmin Champlin –
Can this simulation predict the pressure drop across the microchannel?
MR CFD Support –
Yes, our simulation can provide detailed information on the pressure drop across the microchannel, which is a key factor in understanding the performance of the microchannel.