Two-Blade Savonius Wind Turbine CFD Simulation (2-D)
$140.00 Student Discount
- The problem numerically simulates Savonius Vertical Axis Wind Turbine using ANSYS Fluent software.
- We design the 2-D model by the Design Modeler software.
- We Mesh the model by ANSYS Meshing software, and the element number equals 58468.
- We perform this simulation as unsteady (Transient).
- We use the Mesh Motion model to define rotational motion.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Savonius (Two-Blade) Wind Turbine, CFD Simulation (2-D) Ansys Fluent Training
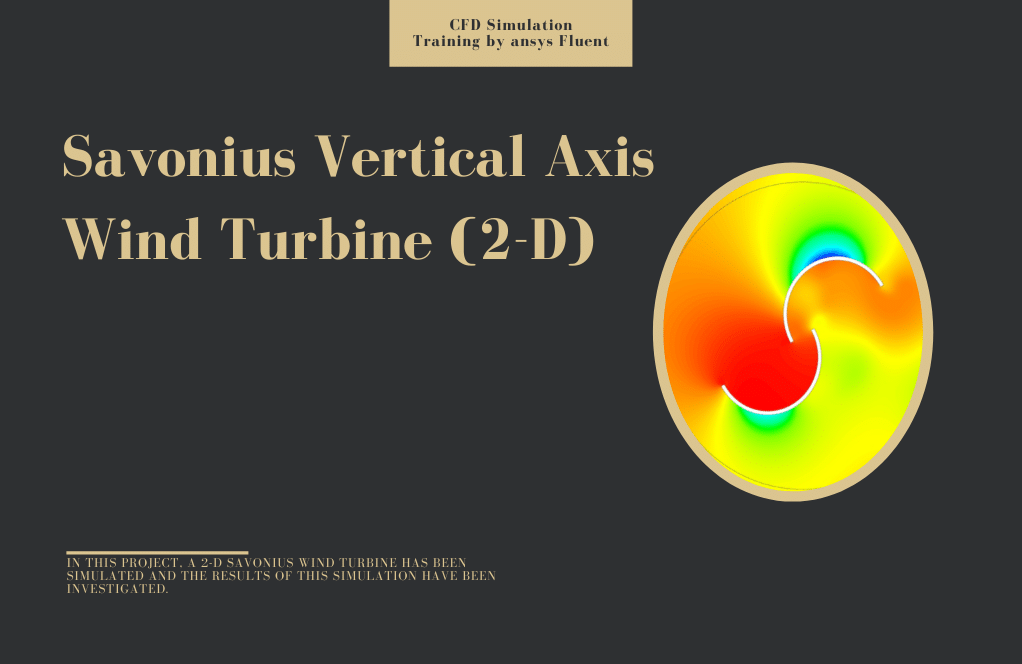
In this project, a 2-D Savonius Wind Turbine has been simulated, and the simulation results have been investigated by ANSYS Fluent software. We perform this CFD project and investigate it by CFD analysis.
The savories wind turbine is a type of vertical axis wind turbine (VAWT) used to generate electricity from wind energy. The turbine consists of several curved airfoil blades mounted on a rotating shaft or framework. In this type of turbine, the main rotor is positioned vertically.
The most important advantage of vertical wind turbines is that they do not need to be adjusted to the wind direction and can also be used at low altitudes.
The three-dimensional geometry of this project has been produced with Design Modeler software. Two blades with 350mm diameter and 25mm thickness located in a rotating circle with 1000mm diameter surrounded by 8000mm*4000mm rectangle were sketched.
We carry out the model’s meshing using ANSYS Meshing software. The element number is 58468.
Also, the transient solver is enabled due to the present problem in which we have used the mesh motion option.
Savonius Methodology
In this project, a two-blade Savonius wind turbine was simulated using mesh motion in Ansys Fluent software, and the results were investigated. Air enters the fluid domain from the inlet with 10m/s velocity while the turbine rotates with a constant angular velocity of 40rpm.
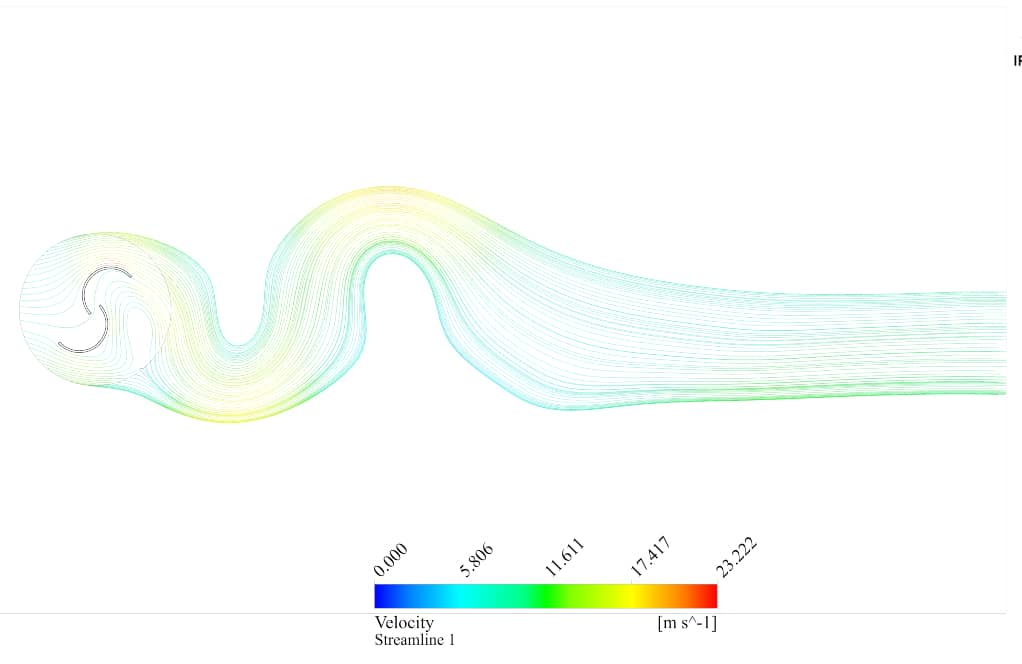
Our final goal is to illustrate the pressure and velocity distribution and animate the fluid motion behind the turbine. Moreover, the SST k-omega model can solve turbulent fluid equations due to its advantage in capturing fluid flow patterns near and far from the blades’ surfaces.
Savonius Conclusion
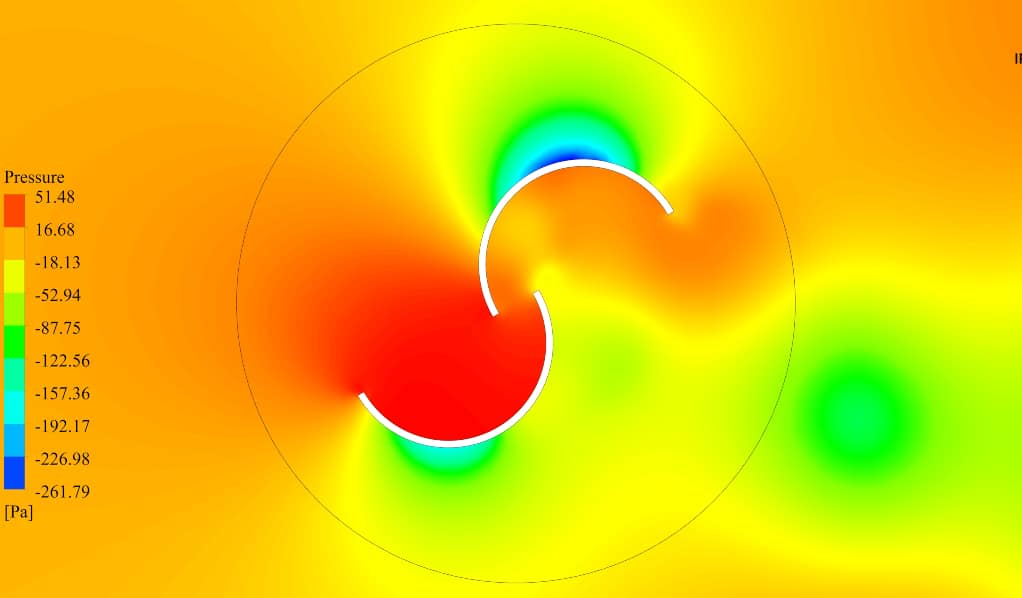
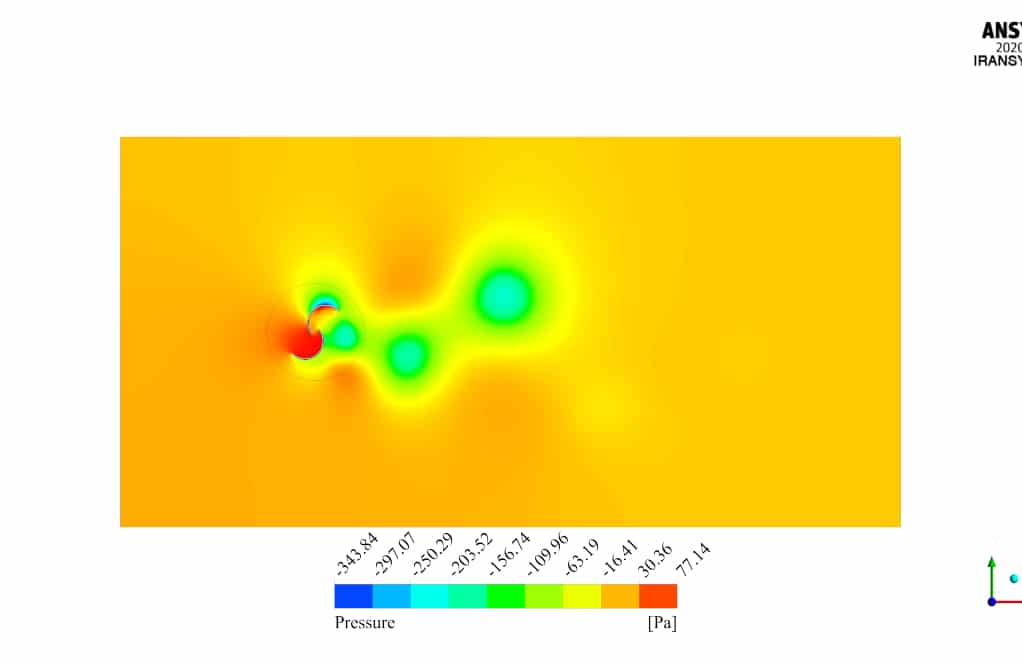
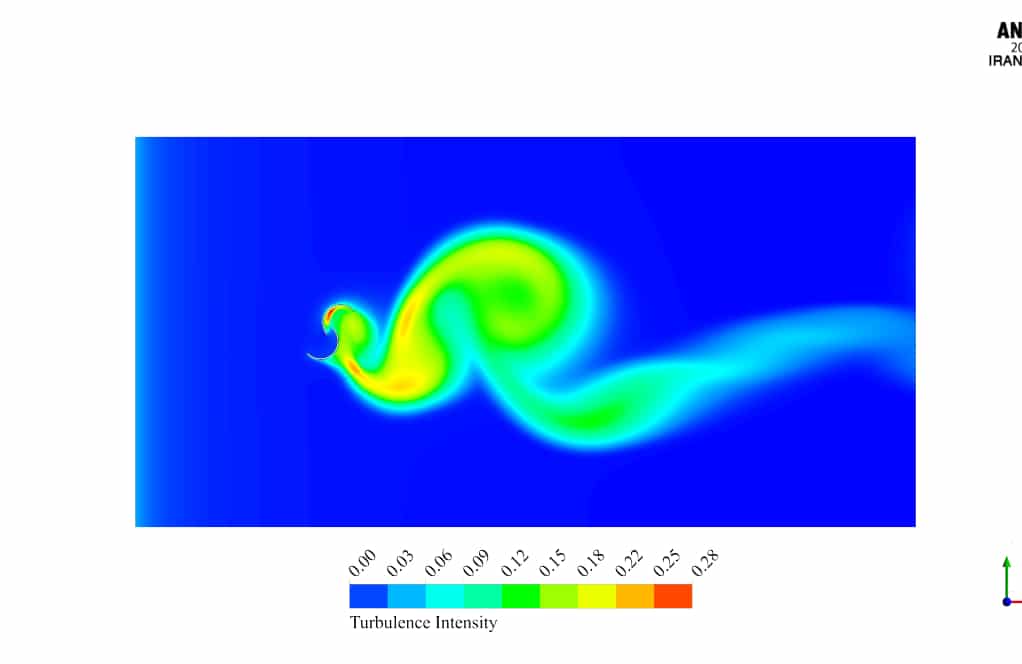
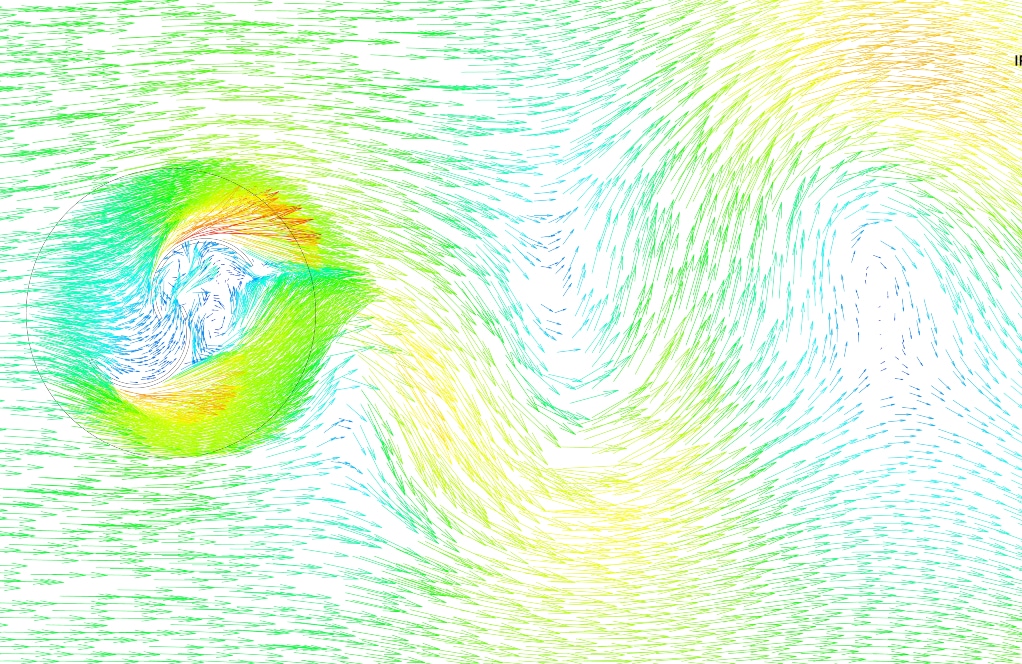
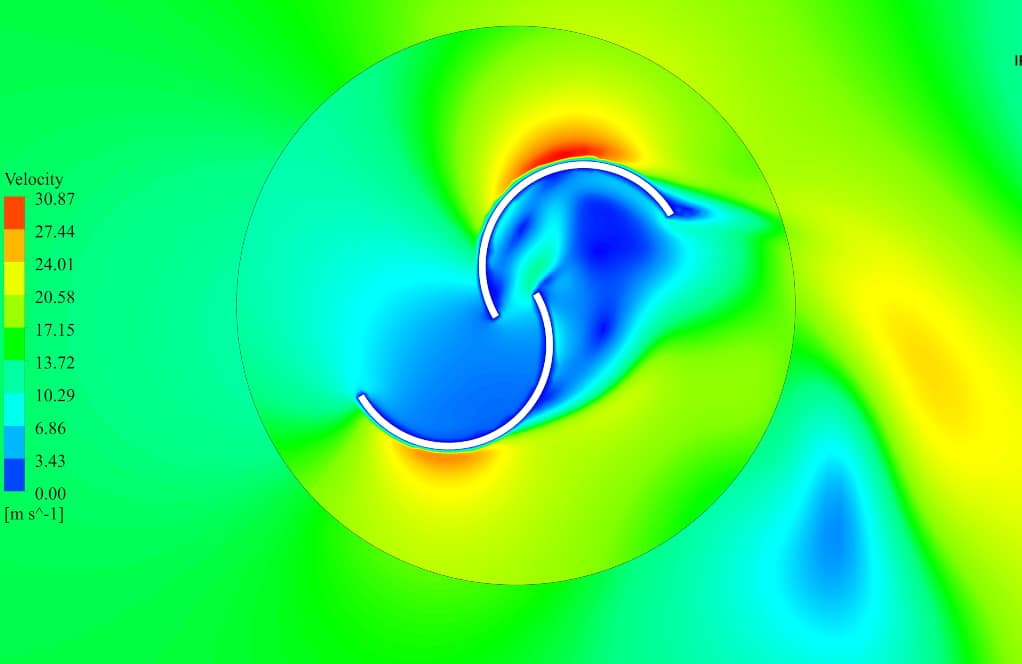
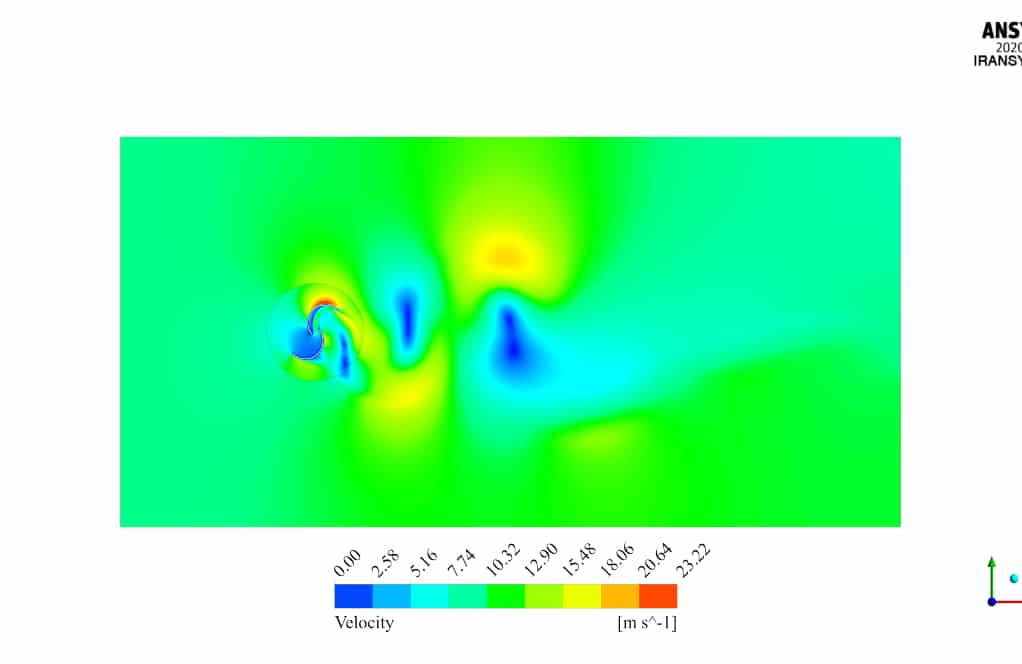
After the solution, two-dimensional contours related to the pressure, velocity, and streamlines are obtained. Figures in this product gallery show a variety of contours of fluid changes during its motion through turbine blades.
According to the results, pressure and velocity distribution are distinctly different in the inner and outer blades. The flow enters the domain with 10m/s velocity.
After the collision with the inner blade, a tremendous pressure increase occurs, so the velocity magnitude decreases and reaches zero at a point known as stagnation point; This may cause negative torque that is not our preference.
On the other hand, the outer blade experience a high-velocity flow on its back, which tends to push the blade clockwise.
Mr. Jaylan Erdman MD –
The explanation of the Savonius turbine simulation is fantastic, especially understanding the velocity impacts on blade performance. Will you be showing a comparison between simulated results and real-world data to verify the accuracy?
MR CFD Support –
Thank you! While we focus on providing detailed simulations, the product you’re reviewing demonstrates the performance of a Savonius turbine within a controlled simulation environment. Typically, there are more extensive studies or additional steps necessary to directly validate simulation results with real-world data, which includes empirical measurements and field tests. Although not detailed in this specific product, comparative analysis is usually a critical phase of CFD projects for modeling real-life behavior. For this particular educational training, real-world data validation may not be included, and the focus is more on understanding the simulation aspects using ANSYS Fluent tools.
Ms. Ardith Renner Jr. –
Can you explain the term ‘negative torque’ mentioned in the conclusion overview?
MR CFD Support –
Negative torque in the context of a wind turbine refers to the opposing force that acts against the desired rotational movement. It is typically caused when airflow generates pressure on part of the structure that results in a force that pushes in the opposite direction to the rotation generated by wind energy. This can reduce the overall efficiency of the turbine since some of the energy from the wind gets used in dealing with this counterproductive force.
Alexandria Blanda –
I found the results fascinating! The impact of pressure and velocity variations on turbine efficiency seems complex. Could you explain how these factors influence the overall efficiency of the wind turbine?
MR CFD Support –
Admin
Dr. Salvador Nicolas –
I am thoroughly impressed by the details offered in the course regarding the pressure and velocity distribution around the Savonius turbine blades. The visuals are truly informative, displaying the stark contrasts in flow patterns, which provide clear insights into optimization opportunities for a Savonius design. Furthermore, the explanation about the stagnation point was very enlightening. Great learning experience!
MR CFD Support –
Thank you for the positive feedback! It is fantastic to hear that the course gave you a clear understanding of the Savonius wind turbine dynamics and helped you to see the detailed pressure and velocity distributions. Your insights are valuable, and we’re glad the visuals were informative and contributed to your learning experience. If you have further interests or questions in the future, do not hesitate to reach out!
Mrs. Vickie Considine PhD –
The detailed flow dynamics around the wind turbine blades and the occurrence of the stagnation point were quite intriguing. This conclusive data helps to visualize the performance characteristics of the Savonius turbine design effectively.
MR CFD Support –
Thank you for your positive feedback! We’re glad to hear that our simulation could provide insightful visualizations into the flow dynamics and make the intricate details like stagnation points comprehensible. Appreciating how those factors influence turbine performance is crucial for design and analysis. If you have any further questions or require additional insights into CFD simulations, feel free to reach out!
Yasmine O’Reilly –
I’m super impressed by the level of detail that comes with the results, especially how the presence of the stagnation point is depicted in the simulations. It’s interesting how VAWTs can operate irrespective of wind direction. Incredible how this complexity is captured in 2D simulation.
MR CFD Support –
Thank you for your positive review on the Two-Blade Savonius Wind Turbine CFD Simulation. We are delighted that you appreciate the complexities and details captured in the 2D simulation results. It’s our aim to provide thorough insights into the turbine’s operational mechanics, and we’re glad it met your expectations!
Jimmie Trantow MD –
This product truly brings the concept of CFD in wind turbine design to life! The detailed explanation of the Savonius wind turbine dynamics and clear visualizations in the simulation make it an exceptional learning tool.
MR CFD Support –
Thank you for your positive feedback! It’s great to hear that our simulation of the two-blade Savonius Wind Turbine in ANSYS Fluent has provided you with a dynamic and thorough understanding of CFD in wind turbine design. We’re pleased that our product has met your learning needs.
Nelson Kirlin –
I am very impressed with the realistic simulation of the two-blade Savonius wind turbine. The results on pressure and velocity distribution offer valuable insights into the turbine’s performance in generating electricity. The animated fluid motion is a great touch for visual learners like me.
MR CFD Support –
Thank you for your positive feedback! We’re thrilled to hear that our CFD simulation of the Savonius wind turbine proved helpful and informational to you. Your appreciation for the detailed pressure and velocity distribution as well as the animated fluid motion encourages us to continue delivering high-quality simulations for our learners.
Haskell Abshire –
This project really showcases the power of CFD in visualizing and understanding fluid dynamics around wind turbine blades. The detail in pressure and velocity distribution is critical for improving turbine design.
MR CFD Support –
Thank you for your positive feedback! We are delighted to hear that our CFD simulation project met your expectations and provided you with valuable insights into the behavior of airflow around the Savonius Wind Turbine. It’s great that the detail presented helped you grasp the intricacies of turbine design. We are committed to helping our customers gain a deeper understanding of fluid dynamics, and your satisfaction is our priority. If you have further questions or need assistance with any other project, feel free to get in touch.
Stephania Donnelly –
I am thoroughly impressed with the detailed analysis and comprehensive nature of the 2-D Savonius Wind Turbine simulation. The use of realistic wind speeds and rotation rates in the simulation, along with capturing the intricate pressure and velocity distributions around the blades, provides invaluable insight into the performance of this VAWT design. The contour figures were particularly helpful in visualizing fluid behavior across the turbine and understanding the impact of blade positioning on the generated torque. Outstanding work!
MR CFD Support –
Thank you for your kind words! We’re delighted to hear that the CFD simulation of the two-blade Savonius Wind Turbine provided you with clear insights into the functioning and efficiency of vertical axis wind turbines. We appreciate feedback on the contour figures, as we strive to ensure that the visual aspects of our training complement the technical details for a better learning experience. If you have further feedback or require assistance with similar projects, please reach out to us.
Ms. Adele Labadie –
I’m impressed by the clear explanation of the Savonius wind turbine simulation. The visualization of pressure and velocity changes as simulated in ANSYS Fluent is a testament to the quality of analysis that can be expected with MR CFD’s materials.
MR CFD Support –
Thank you for your positive review! We are delighted to hear that our explanation and analysis of the Savonius wind turbine simulation met your expectations. It’s gratifying to know our educational materials are helping customers like you understand and visualize key concepts in CFD. If you have any more feedback or need further assistance, please don’t hesitate to reach out.
Luigi Hyatt –
I’ve been doing a study related to Savonius Wind Turbines and your product description is quite informative. Does the simulation take into account dynamic changes in wind direction or it only covers constant wind flows from one direction?
MR CFD Support –
In this 2-D simulation of the Savonius Wind Turbine, we have considered a consistent wind flow entering the domain from one direction at a stated velocity. We currently have not incorporated dynamic wind direction changes in this study, as it typically requires a more complex, possibly 3-D, simulation framework to accurately capture such effects.