Eulerian Two Phase Flow within a Convergent-Divergent Channel, ANSYS Fluent
$80.00 Student Discount
- The problem numerically simulates the Two-Phase Flow within a Convergent-Divergent Channel using ANSYS Fluent software.
- We design the 3-D model with the Design Modeler software.
- We mesh the model with ANSYS Meshing software.
- The mesh type is Structured, and the element number equals 175500.
- We use the Eulerian Multiphase model to define the two-phase flow.
Click on Add To Cart and obtain the Geometry file, Mesh file, and a Comprehensive ANSYS Fluent Training Video.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Description
The problem simulates two-phase flow as soluble particles in a given fluid in a channel with a convergent-divergent structure by ANSYS Fluent software.
The current model is designed in three dimensions using Design Modeler software. The model consists of a channel with a rectangular cross-section with dimensions of 0.001 m * 0.0002 m, which in its longitudinal direction, the geometric structure of the model becomes convergent-divergent.
The meshing of the present model has been done using ANSYS Meshing software. The mesh type is structured, and the element number is equal to 175,500.
Eulerian Methodology
The Eulerian multiphase model has been used to simulate the present model. The Eulerian multiphase model is considered the most complex model for defining multiphase flows.
This model solves a set of momentum and conservation equations for each phase separately, While the multiphase mixture and VOF methods only solve the equations for phases other than the initial phase.
We apply the Eulerian model in applications such as bubble columns, droplet flows, particle-laden flows with a volume fraction greater than ten percent, pneumatic transitions for granular liquid flows, fluidized beds for solid-gas slurry flows, particle suspension and sedimentation phenomena as solid-liquid flows.
In this simulation, the base fluid is defined as a liquid with a density of 1050 kg/m3 and a viscosity of 0.000024997 kg/m.s, and the secondary fluid in the form of particles with a density of 1050 kg/m3 and a viscosity of 1. kg/m.s is defined.
The type of particle dispersion in the base liquid is defined in granular form, and the particle diameter is defined as 0.00002 m. The base fluid and its soluble particles enter this channel at a rate of 0.007142 m/s.
Eulerian Conclusion
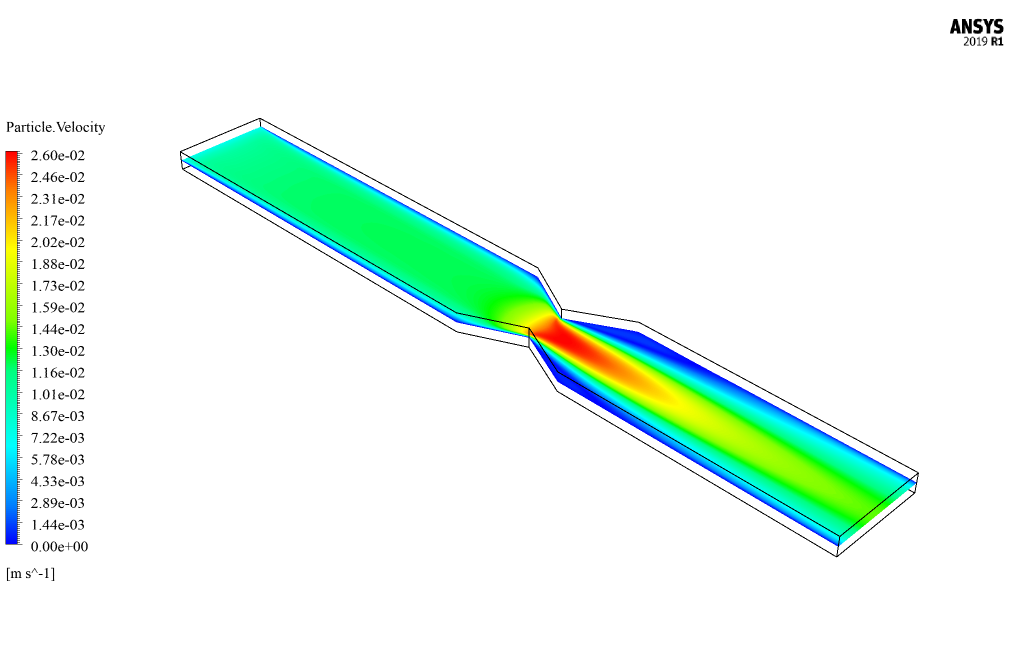
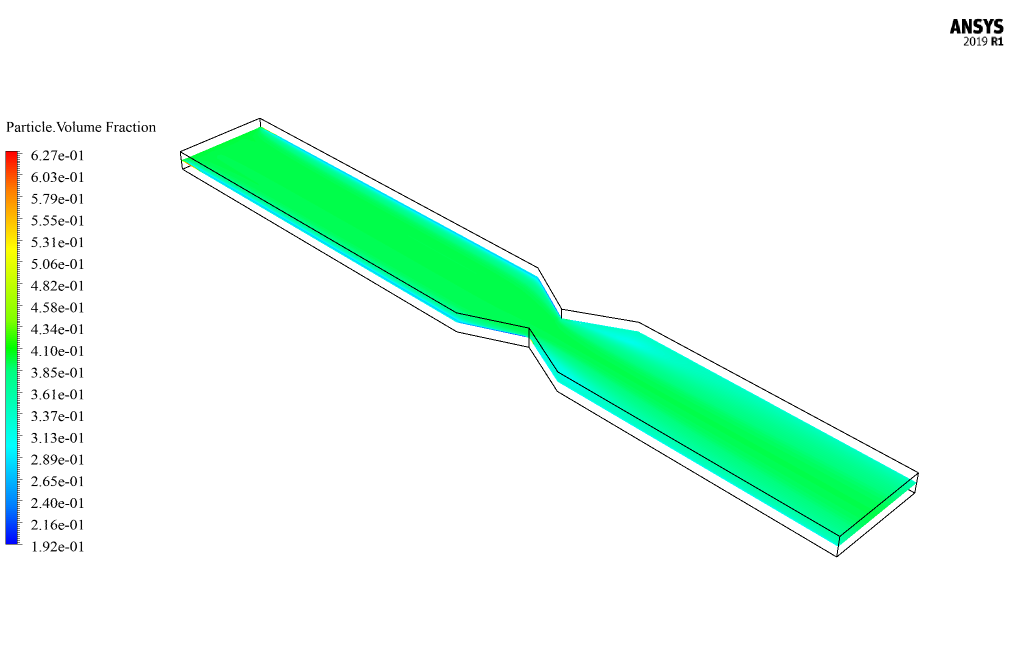
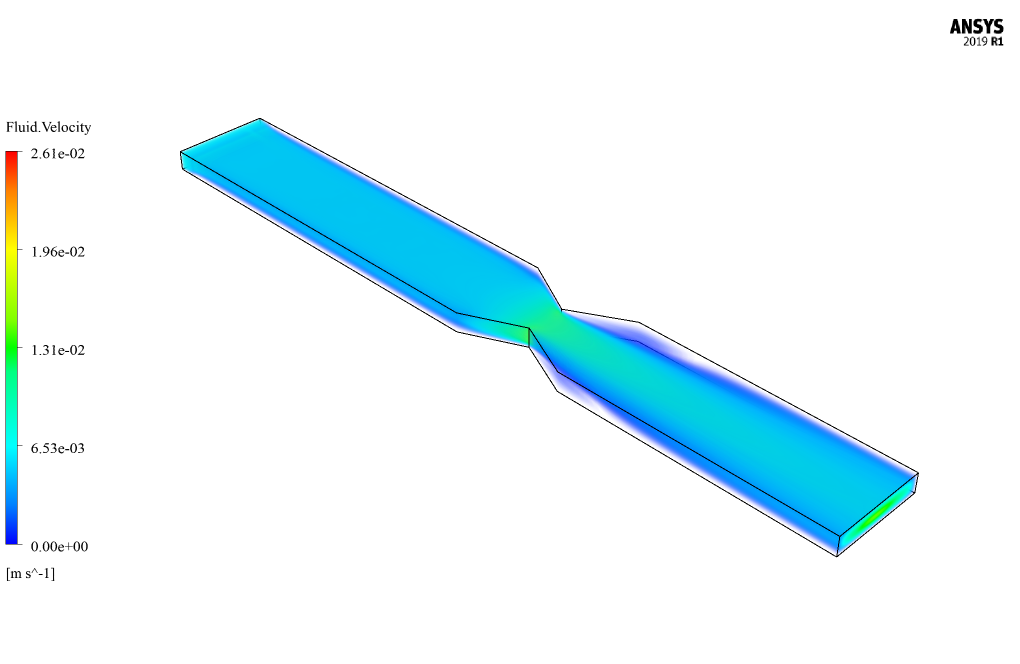
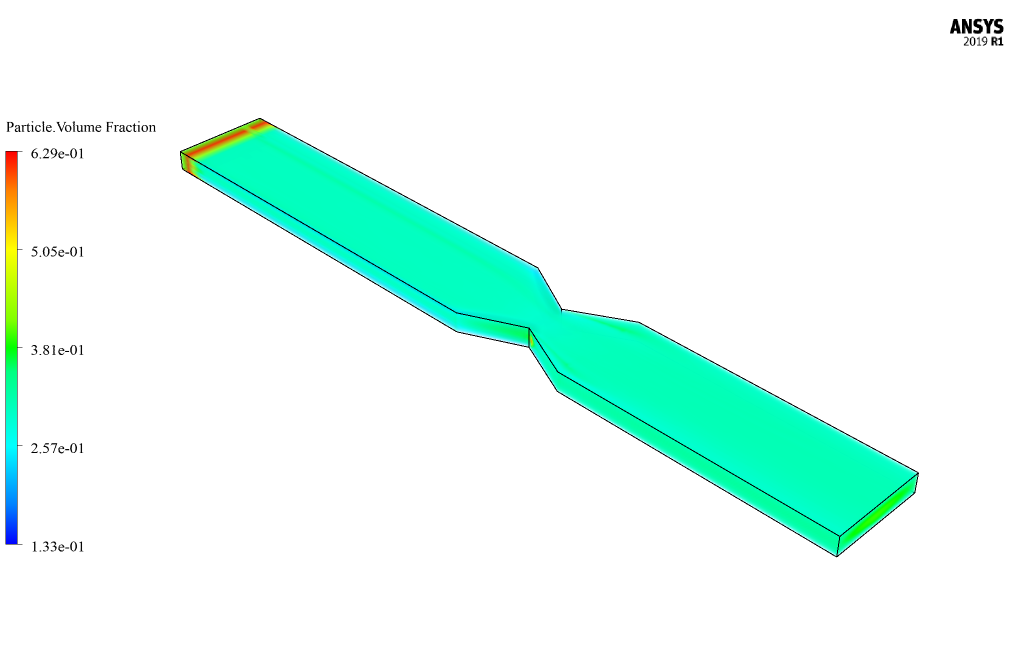
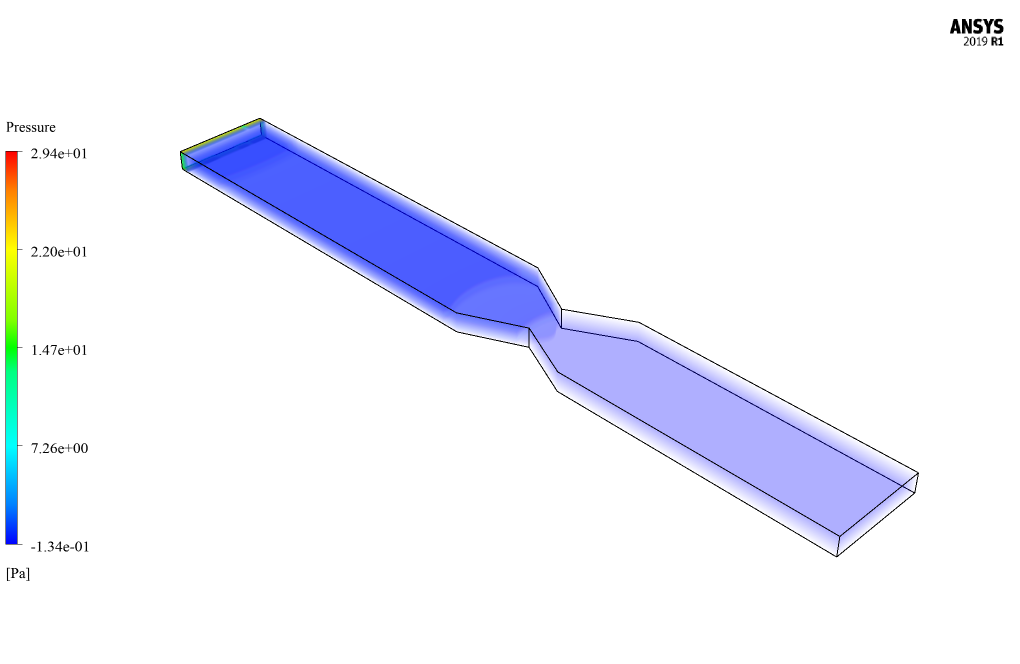
At the end of the solution process, two-dimensional and three-dimensional contours related to the mixing pressure, base fluid velocity, soluble particle velocity, and volume fraction of soluble particles are obtained.
As it is obvious, the maximum velocity occurs in the throat zone since the cross-section is minimum in this section.



Filomena Bernhard DDS –
The explanation is really clear, especially regarding the Eulerian multiphase model. But how exactly did you account for the particle-fluid interaction in the simulation?
MR CFD Support –
In the simulation using the Eulerian multiphase model, the interaction between the particle phase and the fluid phase is accounted for through interphase momentum exchange coefficients. These include drag force, lift force, virtual mass force, and other relevant forces. The computational model solves separate momentum conservation equations for each phase while also considering these exchange coefficients to account for the interactions.
Otto Wolf –
I’m particularly impressed by the level of detail around the Eulerian multiphase model simulation—particularly the part where different density and viscosity parameters were allocated for each phase based on real-world application scenarios. Great to see how numerical simulations can complement laboratory work.
MR CFD Support –
Thank you for the kind words! We appreciate your attention to the detail of our Eulerian multiphase model simulation. It’s indeed our aim to create robust and accurate simulations that can be complementary to experimental testing. We are delighted that you found our product impressive and useful.
Macy Dare –
Really impressed with the level of detail in simulating the flow through a convergent-divergent channel. Everything was well explained and the illustrations added to my understanding.
MR CFD Support –
We’re thrilled to hear that you found the simulation detailed and informative. Your comprehension of the process is a testament to the quality of our learning materials. Thank you for your positive review!
Yadira Wisoky –
The detailed simulation of the convergent-divergent channel is impressive. It has provided clear insights into complex fluid dynamics and the effects of channel geometry on flow patterns.
MR CFD Support –
Thank you for your kind words! We’re pleased to hear the simulation exceeded your expectations and offered you valuable insights. We pride ourselves on delivering in-depth analyses that help our customers understand the intricacies of fluid behaviors. If you have any further questions or need assistance with similar projects, please do not hesitate to reach out!
Hayley Gutmann –
I found the explanation of the Eulerian multiphase model and how it works in your simulation incredibly intriguing! The detailed setup offers a clear insight into complex fluid interactions.
MR CFD Support –
Thank you for your kind words! We’re thrilled that our detailed explanation of the Eulerian multiphase model in the convergent-divergent channel simulation was helpful to you. At MR CFD, we strive to provide clear and thorough details, so it’s great to hear that you found this insight into fluid dynamics both interesting and useful. If you have any more questions or need further assistance on such complex simulations, we’re always here to help!
Lelah O’Reilly III –
This case study of Eulerian two-phase flow simulation in a convergent-divergent channel by ANSYS Fluent was brilliant. The level of detail provided great insight into the setting up of multiphase models using the Eulerian approach. The explanation of the methodology was thorough and enlightening—elucidating complex concepts in a way that’s palatable for a non-expert audience. The results, especially the discovery of maximum velocity in the throat zone and how that impacts the mixing process, were particularly intriguing. It showcased a complex simulation with practical applications, executed meticulously well.
MR CFD Support –
We appreciate your thoughtful review and are pleased to hear that the case study on Eulerian two-phase flow simulation was not only insightful but also well-received. It’s excellent to know that the balance between detailed methodology and the clarity of presentation made the complex simulation concepts more accessible. Your comments on the informative nature of the results, especially regarding the velocity profiles and their effect on mixing within the channel, are very encouraging as well. Thank you for your commendation, and we strive to continue providing valuable and thorough simulations like this one.
Araceli Bernier –
The use of the Eulerian model clearly indicates highly detailed simulations. I am curious, how were particle collisions managed in the flow, considering the concentrated particle regime in certain sections of the channel?
MR CFD Support –
In the Eulerian two-phase flow simulation, particle collisions are managed through the kinetic theory of granular flow which accounts for particle-particle interactions. The simulations use parameters such as granular temperature, collisional viscosity, and pressure to model these interactions and track the dispersed phase’s behavior within the convergent-divergent channel. Depending on model setup, appropriate drag functions and restitution coefficients are also configured to simulate particle-particle and particle-wall collisions realistically.
Rory Jaskolski II –
The description of the Eulerian model approach is thorough. I am especially interested in understanding how granular particle dispersion was handled in the simulation. Can you explain this in more detail?
MR CFD Support –
In this Eulerian model simulation, granular particle dispersion is handled by defining secondary fluid particles with specified density, viscosity, and diameter. This allows the software to track the discrete solid-like particles within the flow by solving momentum and conservation equations for this phase separately. The computational methods tackle the interactions between particles and fluid, as well as the particle collision and transport dynamics within the convergent-divergent channel.
Gina Tremblay –
This CFD project seems complex. Could you please explain if the subsurface rock layers were incorporated into the model?
MR CFD Support –
As this model simulates two-phase flow within a convergent-divergent channel and the substances involved are a liquid and particles, there’s no direct incorporation of subsurface rock layers in the simulation. The focus is on the flow dynamics and particle interactions within the specified channel structure.
Prof. Lexie Stiedemann –
The two-phase flow simulation table ended up being very detailed and helpful. I appreciated the clear explanation of the Eulerian methodology!
MR CFD Support –
Thank you for your positive feedback! We’re delighted to know that the detailed explanation of the Eulerian multiphase model and its application in the convergent-divergent channel simulation was helpful to you.
Violet Gislason –
I’m impressed with the details of this simulation. What specific insight into multicomponent mixing does this type of simulation provide?
MR CFD Support –
The administrative team at MR CFD appreciates your positive feedback! This type of simulation can provide detailed insight into the behavior of multicomponent mixing processes. Factors such as mixing efficiency, flow patterns, the interaction between different phases, and zones of high concentration or velocity can be analyzed. Understanding these parameters helps in optimizing industrial processes where different materials are combined, ensuring uniform mixing and minimizing material waste.
Dr. Camden Wintheiser DVM –
This comprehensive outline really helped me understand the physics behind two-phase flow. However, I’d like to know how the convergence of the soluble particles was accounted for in the simulation. Could you elaborate on that aspect?
MR CFD Support –
In the simulation, convergence of the soluble particles within the fluid was ensured through adequate discretization and iteration methods. Since the Eulerian model solves a separate set of momentum and conservation equations for each phase, this allowed for closer monitoring and adjustments within the iteration process to ensure the convergence of the particle phase with the liquid phase, maintaining accuracy in representing the particle suspension and interaction with the fluid.
Miss Jada Roob –
I am impressed by how detailed the simulation design is. It’s incredible to see the level of precision in creating a convergent-divergent channel and analyzing two-phase flow.
MR CFD Support –
Thank you for your positive feedback! We put a lot of effort into ensuring our simulations are detailed and as accurate as possible. It’s great to hear that our work is appreciated. If you have any further insights or need assistance with your projects, feel free to reach out.
Lorna Nicolas –
I was truly intrigued by this experiment’s ability to predict particle behavior. Could these findings extend to multimaterial injection systems? Would it help in optimizing those processes?
MR CFD Support –
Absolutely, the insights gained from the simultaneous flow analysis of particles and a liquid base in this type of channel geometry can be applied to enact improvements in multimaterial injection systems. By understanding the localized variances in particle-laden flow, such systems can be carefully calibrated to ensure even distribution and minimize risk of clogging or uneven mixing, which is pivotal in optimizing injection processes across various industries.
Cordelia Marks II –
The Eulerian multiphase model seems like the right choice for such a complex simulation. The clarity and detail provided in the review were very helpful.
MR CFD Support –
Thank you for your positive feedback! We’re thrilled to hear you found the details in the review helpful. If you have any more questions or need further information on our simulations, please feel free to reach out.
Lorna Paucek –
The tutorial on Eulerian two-phase flow within a convergent-divergent channel was excellent. It really clarified how the multiphase model works, and the visuals helped to understand the flow dynamics in each section of the channel. Great material for a deeper grasp of CFD applications.
MR CFD Support –
Thank you for the positive feedback on our Eulerian two-phase flow simulation tutorial! We’re thrilled to hear that our materials and visual aids have helped enhance your understanding of multiphase models and CFD applications. Your satisfaction is very important to us, and we appreciate your compliment.
Hudson Harris –
The tutorial was really clear in demonstrating how to set up a focused convergence simulation. Thanks to this, I was able to replicate the results in my own project!
MR CFD Support –
Thank you for your kind words! We are delighted to hear that our tutorial was helpful for your project and that you were able to successfully achieve your simulation objectives. If you have any further questions or need additional assistance, feel free to reach out. Your success is our top priority.
Miss Kendra Russel Sr. –
I’m truly amazed by the level of detail of the flow patterns depicted in the contours. Well done in showcasing the effects at the throat zone clearly.
MR CFD Support –
Thank you for your positive feedback! We’re delighted to hear that you found the detailed representation of flow patterns and their effects in the throat zone clear and informative. Our team strives to provide high-quality and precise simulations, and it’s rewarding to know that our efforts resonate with our customers. If there’s anything else you’re curious about or any further assistance you need, we’re always here to provide support!
Prof. Hermina Sanford –
Just wanted to say that this course helped clarify many concepts about two-phase flow for me. The step-by-step guide on setting up the Eulerian model in ANSYS was particularly useful.
MR CFD Support –
We’re delighted to hear that our training material on the Eulerian two-phase flow within a convergent-divergent channel has been helpful for you. Your mastery of the concepts and positive feedback motivate us to continue providing quality educational content. Thank you for choosing our product!
Earnest Crooks Sr. –
I was fascinated by the way this product captures the challenging dynamics of Eulerian two-phase flows. It is outstanding that the model intricately details the reactions between the two phases, particularly under the morphology of a convergent-divergent channel. Well done on delivering such an insightful computational perspective!
MR CFD Support –
Thank you for your kind words. We are delighted to know that you appreciate the intricacy and detailed analysis provided by our Eulerian two-phase flow simulation product. Your feedback is highly valued, and we strive to continue delivering high-quality and insightful CFD products. If you need further information or assistance, feel free to reach out.
Malcolm Moen –
I found the aspect of simulating flow within a convergent-divergent channel very useful! The detailed application of the Eulerian model is impressive, leading to a comprehensive understanding of two-phase flow phenomena in such configurations.
MR CFD Support –
Thank you for your positive feedback on our simulation of Eulerian two-phase flow within a convergent-divergent channel using ANSYS Fluent. We are thrilled to hear that you found the use of the Eulerian model and the detailed understanding it provides to be impressive and useful. Your appreciation motivates us to continue delivering high-quality educational content and simulation experiences. If you have any further questions or need assistance with your CFD learning journey, please do not hesitate to reach out.
Mr. Gunnar Fahey IV –
I am truly impressed by the problem’s approach to simulating the interactions between soluble particles and the fluid within the complex geometry of a convergent-divergent channel. The attention to detail, especially concerning the Eulerian multiphase model handling, makes it highly educational for understanding multi-phase fluid dynamics!
MR CFD Support –
Thank you for your kind words! We’re delighted that you found our detailed simulation approach using the Eulerian multiphase model educational and useful for understanding complex two-phase flow interactions. It’s great to see our efforts in creating a valuable learning tool are appreciated!
Kailee Ebert –
The results provided by MR CFD’s simulation on the Eulerian two-phase flow within a convergent-divergent channel using ANSYS Fluent were truly insightful. Having access to the detailed pressure and velocity contours as well as the particle volume fraction delivered the clarity needed for understanding complex interactions within the flow domain. It’s commendable how accurately the behavior of soluble particles in the convergent-divergent structure of the channel was captured, particularly the sharp increase in velocity at the throat section. This indicates a thorough and well-executed simulation process.
MR CFD Support –
We’re glad you found the simulation results insightful and commendable! It’s always our goal to ensure that complex fluid dynamics phenomena are accurately represented and easily understandable for our clients. If you have specific follow-up questions or need further details, feel free to reach out. We’re here to help. Thank you for sharing your positive experience with this CFD simulation.
Mr. Randal Waters –
I’m thoroughly impressed by the level of detail provided in the simulation’s results. The visual representation of velocity and pressure variations through the convergent-divergent sections helps in understanding flow properties under such conditions. It’s commendable how the software captures the peak velocity at the throat, which aligns perfectly with fluid dynamics theory.
MR CFD Support –
Thank you for your kind words! We’re thrilled to hear that the detailed information and visualization in the simulation results have enhanced your understanding of the fluid dynamics involved. Your feedback is greatly appreciated and motivates us to continue providing high-quality learning products.