Kaplan Hydro Turbine Evaluation, ANSYS Fluent CFD Simulation Tutorial
$120.00 Student Discount
- The problem numerically simulates the hydrodynamics of the Kaplan turbine using ANSYS Fluent software.
- We design the 3-D model by the Design Modeler software.
- We Mesh the model by ANSYS Meshing software, and the element number equals 9861922.
- We use the Frame Motion to define rotational movement around the Kaplan turbine.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Description
This simulation is about Kaplan hydro turbine evaluation via ANSYS Fluent software. We perform this CFD project and investigate it by CFD analysis.
The Kaplan turbine is a propeller-type water turbine that has adjustable blades. Also, the Kaplan turbine is an inward flow reaction turbine, which means that the working fluid changes pressure as it moves through the turbine and gives up its energy.
Power is recovered from the hydrostatic head and the flowing water’s kinetic energy. The design combines features of radial and axial turbines. In this project, we will study Kaplan turbine hydrodynamics. For the rotating motion of the turbine, we determined an angular velocity equal to 16.5 RPM.
For our boundaries, we set a constant mass flow of 1000 kg/s as our inlet, a zero gauge pressure as our outlet, and finally, we considered all the side walls symmetrical since they are far from the domain of interest.
In this study, we have also investigated the performance of the current Kaplan turbine by evaluating the drag force.
The geometry of the present model is drawn by Design Modeler software. The geometry included a small Kaplan turbine. The model is then meshed by ANSYS Meshing software. The model mesh is unstructured, and 9861922 cells have been created.
Kaplan Method
In this simulation, the MRF (Frame Motion) option has been activated to model the rotation of the turbine. It is assumed that the fluid around the turbine blades is rotating instead of the turbine blades.
Therefore, a cylindrical zone has been separated from the whole computational zone due to having a turbomachinery simulation. The rotational velocity of this fluid is equal to the rotational velocity of the turbine. To do this, the MRF tool is used in Cell Zone Conditions.
Kaplan Conclusion
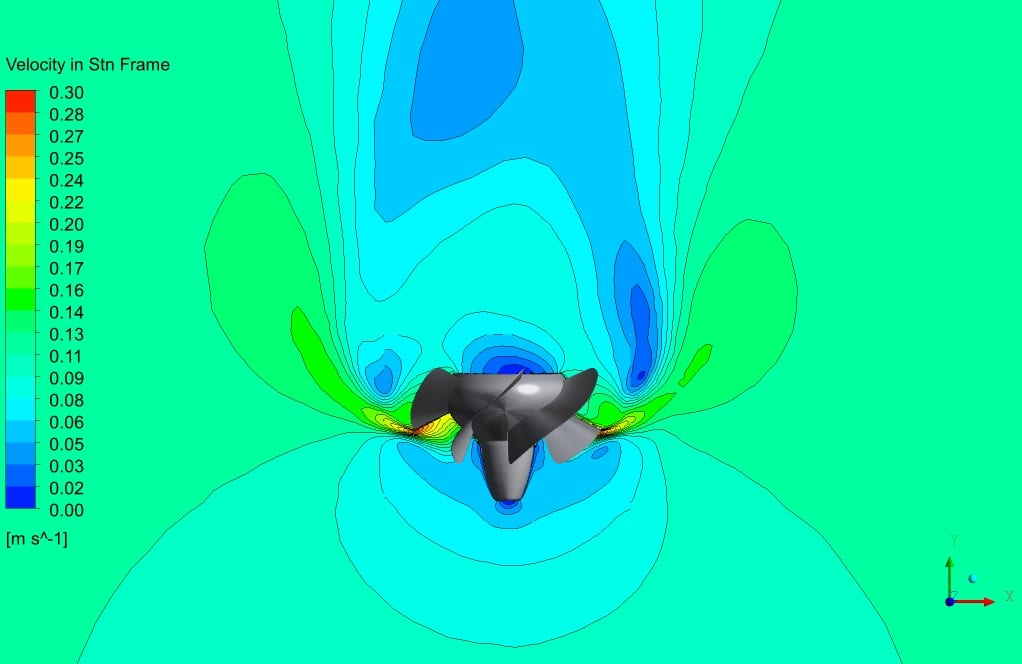
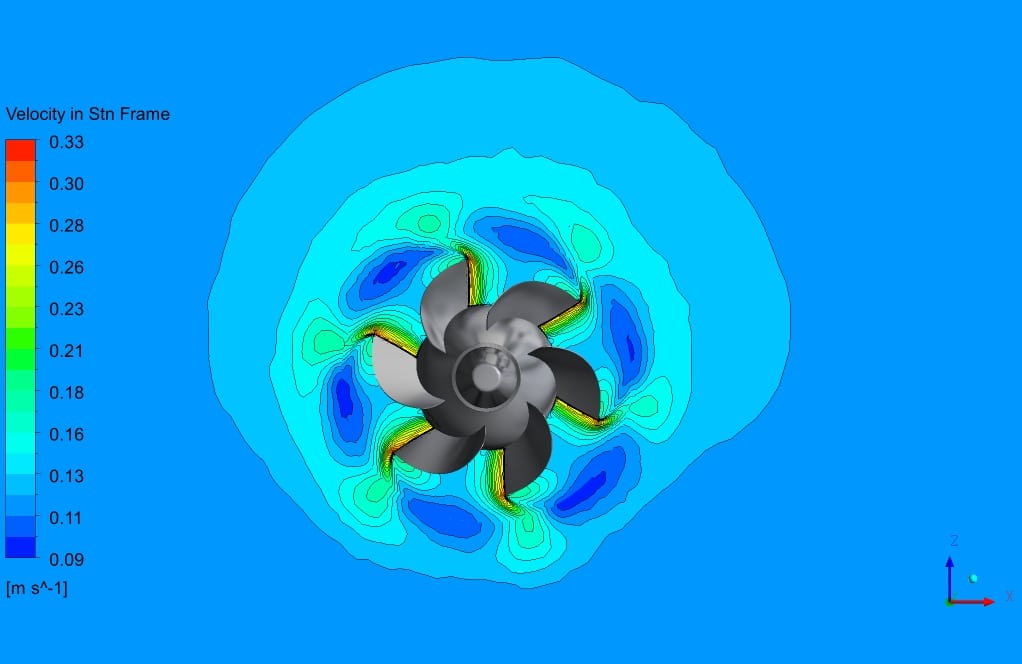
After simulation, 2D and 3D contours of pressure, velocity, and surface pressure are obtained. Also, the velocity vector and streamlines around the turbine are obtained. Velocity vectors and streamlines show the rotational motion of the fluid around the turbine blades.
As depicted in the contours, the leading edge of the turbine wall corresponding to the lowest pressure is entirely logical since the velocity has the highest value on the tip of the turbine blade.
Also, the contours of velocity show that as we go farther from the turbine axis, the rotational velocity and the influence of our source terms would be increased. As depicted in the pressure contours, the pressure distribution adjacent to the turbine walls formed two significant sections.
The first section corresponds to the high-pressure zone before the flow interacts with the Kaplan turbine. The low-pressure zone, however, is the zone behind the Kaplan geometry.
Additionally, the flow vectors illustrate the quality of the flow resolved in the wake section, which is the core challenge of aerodynamic simulation.
Understood from the flow vectors, we have observed the suction mechanism at the lower parts of the turbine, while we have illustrated the blowing mechanism for the upper section.
Moreover, we have given the core vortex adjacent to the turbine body to inform us how the flow field would be manipulated close to our rotary walls.

















Mark Harvey –
The Kaplan turbine project is such an insightful simulation! It goes into great detail about the turbine’s operation and the flow of water around the blades. Through the use of visualization like velocity vectors and pressure contours, I feel like I really understand the intricacies of how Kaplan turbines work. Super impressed with the clarity provided in this learning tool!
MR CFD Support –
We’re thrilled to hear that you found the Kaplan turbine CFD simulation insightful and clear! It’s our goal to provide comprehensive and detailed simulations that enhance understanding in a visually engaging way. Thank you for your positive feedback, and we’re glad that our effort to illustrate the complexities of turbine flow dynamics was helpful to you!
Pablo Wisozk –
The Kaplan Hydro Turbine simulation was exceptional in teaching the intricate hydrodynamics around rotating machinery. It wonderfully demonstrated how fluid behaves in response to the turbine’s movement. The clarity in the setup steps and the detailed visualization of flow patterns were exceedingly helpful in grasping the concepts of turbine evaluation using CFD.
MR CFD Support –
Thank you for your positive feedback! We’re delighted to hear that our Kaplan Hydro Turbine simulation was able to provide you with a clear understanding of hydro turbine dynamics and the evaluation process in ANSYS Fluent. Your appreciation for our visualization and explanation of flow patterns and setup steps is greatly valued.
Vicente Raynor –
Great tutorial! I successfully simulated the Kaplan turbine’s hydrodynamics, and your detailed explanation of setting up the MRF option clarified everything perfectly. The results matched with my expectations, and the visualization of pressure and flow fields was especially helpful in understanding the performance.
MR CFD Support –
Thank you for your positive feedback! We’re pleased to hear our tutorial on the Kaplan hydro turbine simulation was helpful and that the step-by-step guidance on setting up the MRF option made things clear for you. It’s wonderful that the results align with your expectations and that the visualizations enhanced your understanding of the turbine performance. If you need any further assistance or have more questions about CFD simulations, please do not hesitate to reach out!
Tavares Kuhic –
Fantastic resource for understanding Kaplan turbines! The level of detail in process explanation and results discussion is admirable. I particularly appreciate the thorough analysis of the pressure distribution and flow vectors around the turbine blades.
MR CFD Support –
Thank you for your positive feedback! We’re thrilled to hear that our Kaplan hydro turbine evaluation tutorial was so helpful to you. We strive to provide comprehensive explanations and detailed analyses in our CFD projects. If you have any further questions or need more information, feel free to reach out!
Valerie Brown –
The content on Kaplan hydro turbine simulation sounds fascinating! It’s amazing how CFD can be used to analyze the performance of such complex machinery. Great job on thoroughly investigating the aerodynamics and hydrodynamics involved in the design of the Kaplan turbine. The detailed breakdown of simulation setup, method, and analysis of results provides a clear understanding of the project’s scope. It displays the level of expertise in using ANSYS Fluent to its fullest potential. Kudos to MR CFD for delivering a comprehensive simulation tutorial that can aid in enhancing turbines’ efficiencies.
MR CFD Support –
Thank you for your positive feedback! We’re delighted to hear that you find the Kaplan hydro turbine simulation valuable and informative. Our aim is always to provide high-quality CFD simulations and tutorials, ensuring our users clearly understand the complexities involved and how to effectively utilize ANSYS Fluent. If you aspire to further detail or engage in other similar simulations, MR CFD is here to support you. Keep exploring and learning with us.
Kenna Lehner –
The information provided was really insightful. It helped me understand turbine hydrodynamics much better. The detailed explanation of how the velocity contours and streamlines related to the turbine performance was particularly useful. Thank you for this excellent CFD tutorial!
MR CFD Support –
Thank you for your positive feedback! We are delighted to hear that our tutorial on Kaplan Hydro Turbine evaluation was helpful and insightful for you. Understanding the dynamics of turbine hydrodynamics is key for simulations like these, and we’re glad you found the velocity contours and streamline explanations useful. If you have further questions or need more assistance, feel free to reach out!
Chadd Kertzmann –
The Kaplan turbine simulation is splendid. It’s evident that this CFD project was rigorous and the results are highly beneficial for understanding turbine hydrodynamics.
MR CFD Support –
Thank you for your positive review! We’re thrilled to hear that you found the Kaplan hydro turbine evaluation informative and helpful. We take pride in delivering detailed CFD analyses and are glad it is appreciable in our results. Your feedback is very motivating for our team. If you have any further questions or need more insights into our simulations, please feel free to reach out.
Mr. Alex Feest –
I thoroughly enjoyed the in-depth explanation of the Kaplan turbine simulation! The clear presentation of results such as 2D and 3D pressure and velocity contours greatly helped me understand the flow dynamics around the turbine. It’s fascinating to see how the rotational velocity impacts the fluid movement both near the blades and further out from the turbine axis.
MR CFD Support –
Thank you very much for your positive feedback! We’re delighted to hear that our presentation of the Kaplan hydro turbine simulation results was helpful and insightful for you. Understanding flow dynamics is crucial in these simulations, and we’re glad you appreciated the effort. We look forward to providing you with more valuable learning experiences.
Don Kozey MD –
The tutorial for the Kaplan hydro turbine has been insightful! I learned a lot about how these turbines work and the significance of adjustable blades. The detailed explanation of how to use the MRF for simulating rotational motion was very helpful. Great job on providing clear and practical steps for evaluating the turbine’s performance!
MR CFD Support –
Thank you for your positive feedback! We’re thrilled to hear that our Kaplan hydro turbine CFD simulation tutorial was helpful and provided you with a clear understanding of the simulation process and evaluative tools in ANSYS Fluent. We always strive to deliver informative and practical guides. If you have any more questions or need further assistance, feel free to reach out.
Ismael Franecki –
The Kaplan turbine simulation seems very detailed. Can you use this process to accurately predict the actual performance of a full-scale turbine?
MR CFD Support –
Yes, using CFD analysis for the Kaplan turbine as outlined in this process allows us to predict the actual performance with a high degree of accuracy. The detailed mesh and setup capture the essential physics involved in turbine operation. However, it’s crucial to validate the CFD results with experimental or real-world data to ensure accuracy in the prediction.
Prof. Jeanie Wilderman Sr. –
I am thrilled with the Kaplan hydro turbine simulation! The detailed analysis and visuals really helped deepen my understanding of the turbine’s hydrodynamics.
MR CFD Support –
Thank you for your positive feedback! We are glad the simulation met your expectations and provided you with a deeper insight into the performance of the Kaplan hydro turbine.
Susana Roberts DVM –
The Kaplan Turbine simulation tutorial was impressive! The intricate details on the pressure contours, velocity vectors and their interpretation were especially compelling. It was enlightening to see how the flow changes around the blades and the effect of the source terms on rotational velocity. Great job on presenting the influence on aerodynamics within the wake section too!
MR CFD Support –
Thank you for your wonderful feedback on our Kaplan Hydro Turbine Evaluation CFD Simulation tutorial! We truly appreciate your remarks about the presentation and explanation of the pressure contours and velocity vectors. It’s rewarding to know our efforts in detailing the fluid dynamics around the Kaplan turbine blades were enlightening and contributed to a better understanding. Your appreciation for our aerodynamic analysis is greatly valued!