Battery Cooling (Thermal Management) by PCM, ANSYS Fluent Training
$160.00 Student Discount
- The problem numerically simulates the battery cooling by applying phase change material in a storage tank using ANSYS Fluent software.
- We design the 3-D model by the Design Modeler software.
- The present simulation is performed in two steps: without and with phase change material on both sides of the battery.
- We mesh the model with ANSYS Meshing software.
- The mesh type is Structured, and the element number equals 93090 and 276660 for the first and the second cases, respectively.
- We perform this simulation as unsteady (Transient).
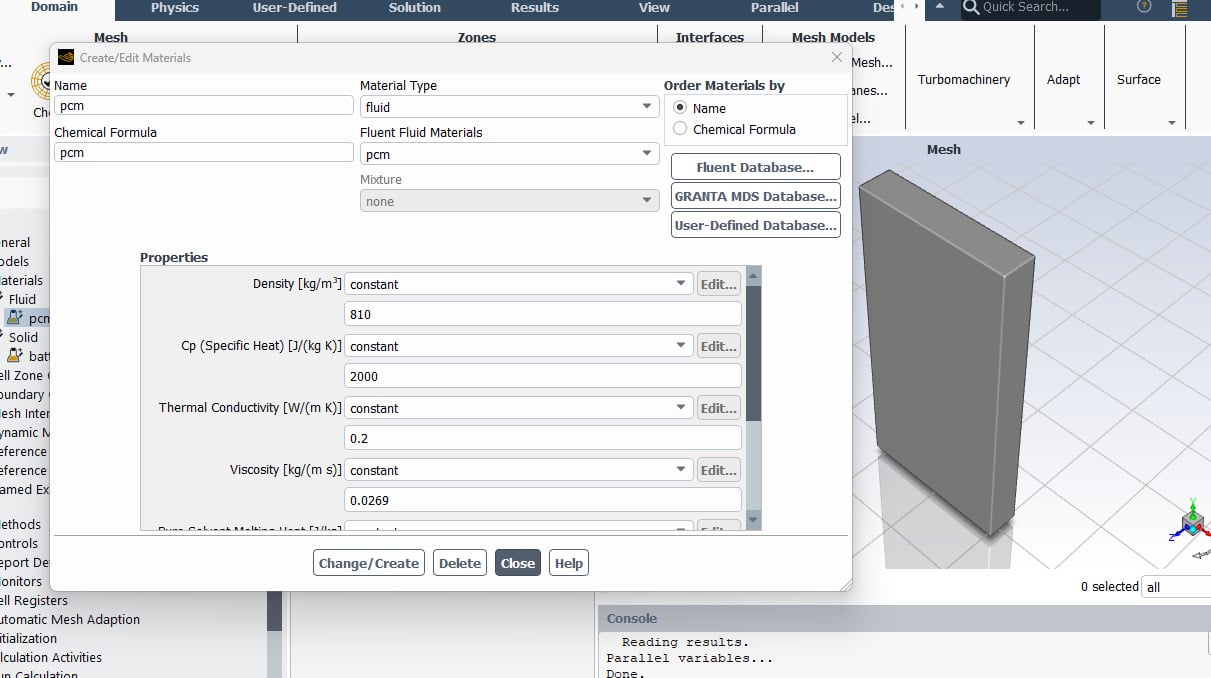
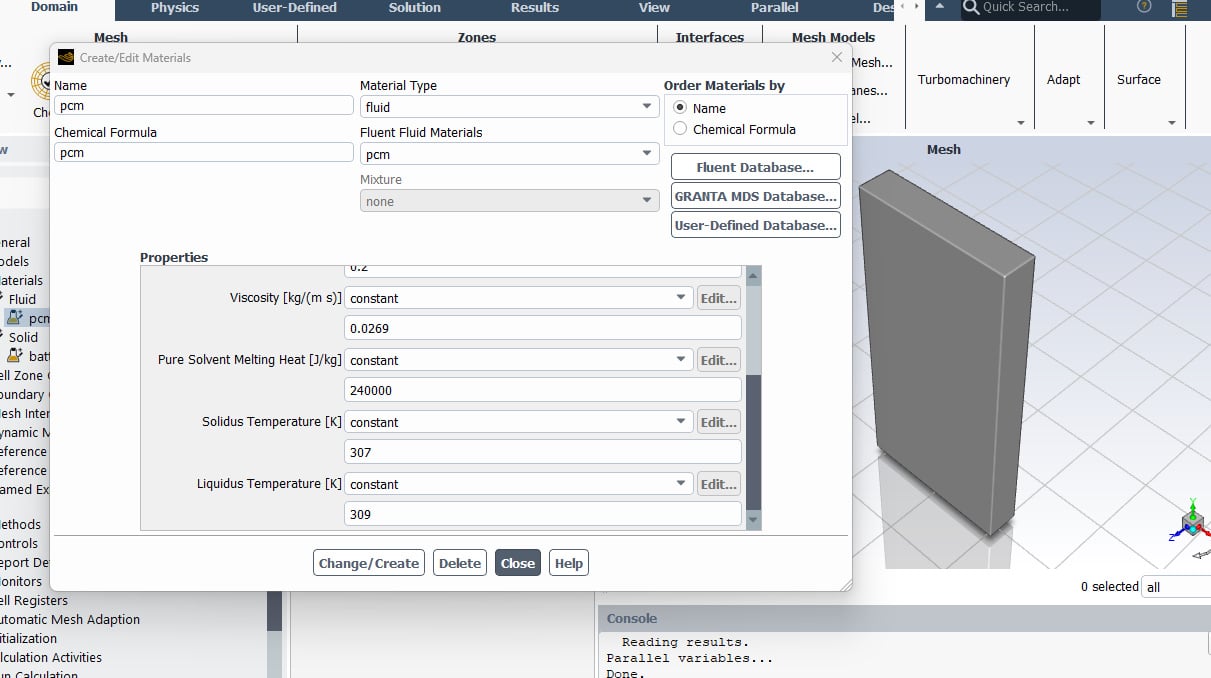
- We use the Solidification and Melting model to define phase change materials.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Description
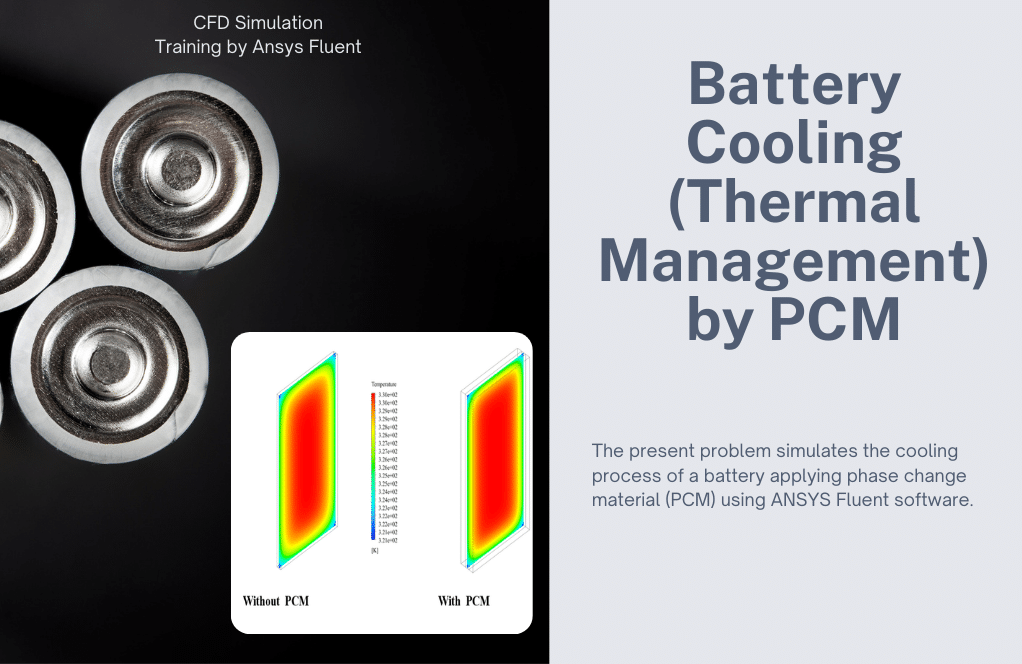
The present problem simulates the cooling process of a battery (battery cooling) by applying phase change material (PCM) using ANSYS Fluent software. We perform this CFD project and investigate it by CFD analysis.
The present simulation is performed in two stages; In the first stage, only one lithium battery is modeled, and in the second stage, two layers of phase change material are used on both sides of the battery.
This work aims to investigate the effectiveness of phase change materials in the cooling process of the battery.
The present model is designed in three dimensions using SOLIDWORKS and then imported into the Design Modeler. We design the geometry in two steps.
The battery designed in the initial modeling has a thickness of 11.3 mm, and its length and width are 335 mm and 167 mm, respectively. In the second model, we add two 12 mm thick layers to both sides of the battery body.
We carry out the model’s meshing using ANSYS Meshing software. The mesh type is Structured. The element number is 93090 and 276660 for the first and the second cases, respectively.
Moreover, due to the nature of the present problem, the transient solver has been enabled.
Battery Cooling Methodology
When the battery starts working, an electric current is established inside it. The current inside the battery can generate heat and increase the temperature of the battery. In this simulation, we define a volumetric heat source in the battery area to determine the amount of heat generation inside the battery.
The heat generated in the battery is equal to R*I², So R is equal to the battery’s internal resistance, and I is equal to the current intensity inside the battery. This modeling assumes that the battery’s internal resistance equals 10 mile-ohms, and the current intensity equals 86 amps.
As a result, the amount of heat generated inside the battery is approximately equal to 120,000 W/m3. In this simulation, the model of solidification and melting is used to define the phase change materials.
To define phase change materials, it should be noted that the maximum temperature at which the solid phase temperature is (solidus temperature) is 307 K, and the minimum temperature at which the liquid phase is dominant (liquidus temperature) is 309 K.
Also, the pure solvent melting heat is defined as 240000 j/kg. Moreover, the laminar model and energy equation are enabled to solve the fluid equations and calculate temperature distribution.
Battery Cooling Conclusion
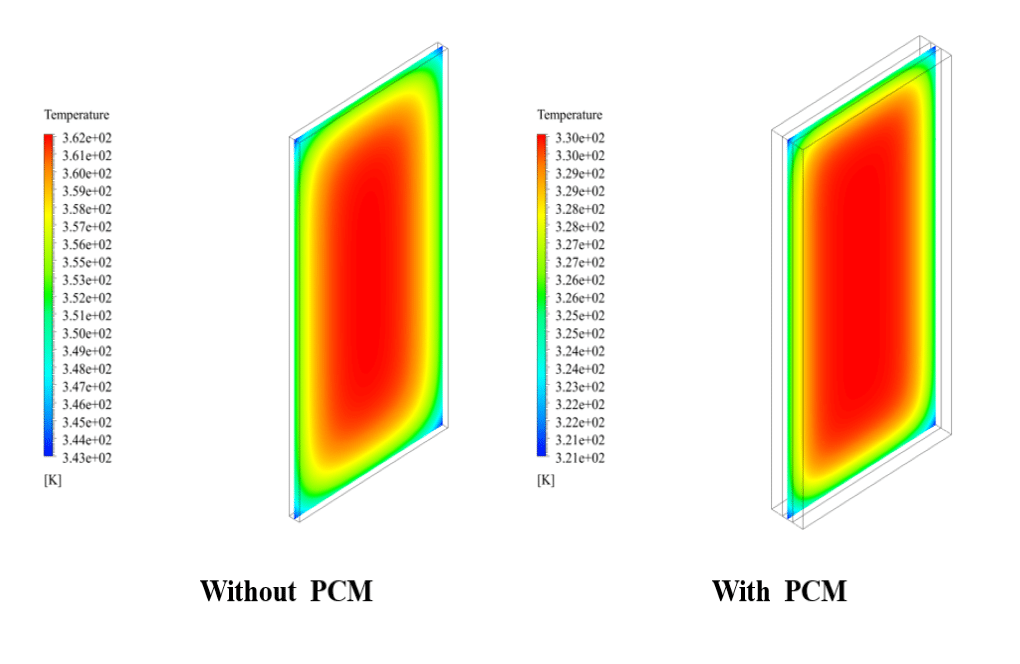
At the end of the solution process, we obtain two-dimensional and three-dimensional temperature contours in both simulation steps. We compare the temperature contours in both stages at the end of the simulation.
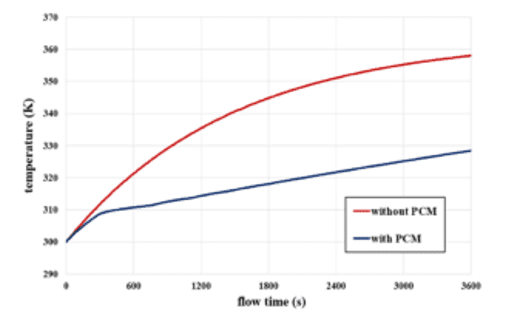
Also, we obtain the diagram of the average temperature changes of the battery in terms of time for the two states with and without phase change material. We present this chart in one hour.
The results show that applying a phase change material coating to the battery body will cool the battery and reduce the temperature growth rate.
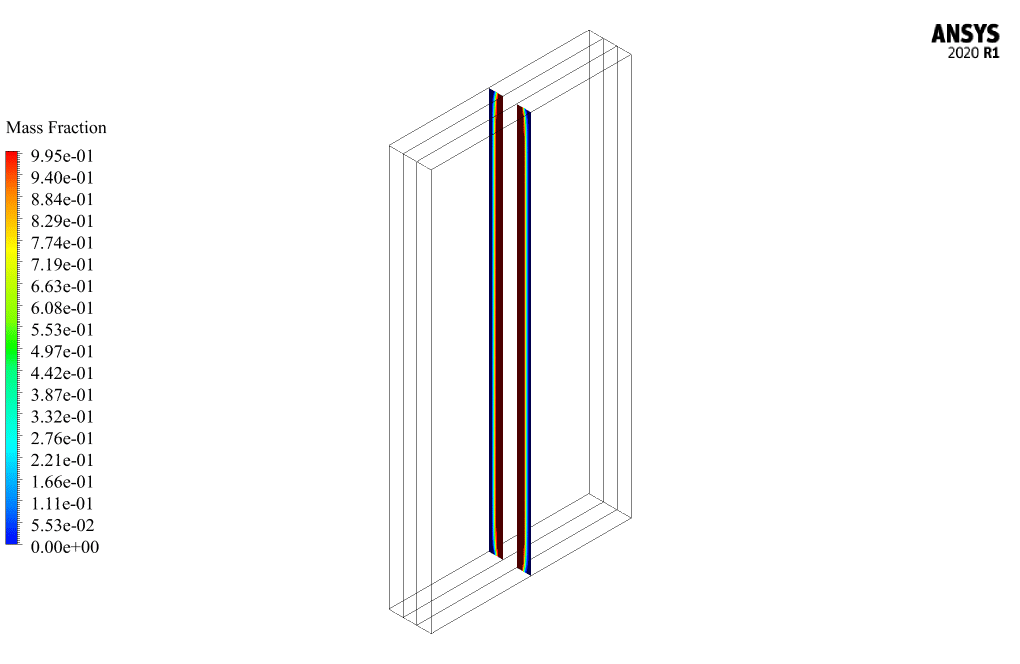
Also, two-dimensional and three-dimensional contours related to the volume fraction of liquid from the phase change material are obtained in the second stage of the simulation to show its effect on heat transfer with the battery body.


Guiseppe Tillman DDS –
I am very impressed by how the thermal management of the battery is simulated using PCM in ANSYS Fluent, as detailed in the coolings process description. This technical approach seems quite innovative and could be valuable for further research and practical applications.
MR CFD Support –
Thank you for your positive feedback! We’re pleased to hear that you found the battery cooling simulation using PCM insightful and useful. It’s our goal to provide comprehensive learning products that can support both academic and industry professionals. If you have any further inquiries or need more information, feel free to reach out!
Elna Mante –
This training was impressively thorough. Learning about battery cooling using PCM was insightful, and the inclusion of different simulation stages added depth to understanding the effectiveness of PCM for thermal management.
MR CFD Support –
Thank you for the positive feedback! We’re very pleased to hear that you found the training on battery cooling using phase change material insightful and the simulation stages helpful. Your understanding of the training materials validates our effort to provide comprehensive educational experiences. If you have further inquiries or need more information, do not hesitate to ask. We’re here to help!
Dr. Devyn Shields I –
I’m still not clear on how the PCM contributes to cooling after phase change, could you please explain?
MR CFD Support –
The PCM helps in cooling by absorbing heat from the battery as it changes from solid to liquid. When the battery heats up due to operation, the heat transfers to the PCM, causing it to melt. This phase transition from solid to liquid requires energy, which is taken from the surrounding heat, effectively reducing the temperature. Once the battery cools down, the PCM solidifies, releasing the absorbed heat in a controlled manner.
Dr. Carmen Schmeler DVM –
I really appreciated the clarity of the explanation on how the heat generation was modeled using R*I^2 for the heat source within the battery. Understanding this aspect is fascinating. Wonderful material for learning how to simulate complex thermal interactions within battery systems!
MR CFD Support –
Thank you for your kind words! We’re thrilled to hear that our product has helped enhance your understanding of thermal management through simulations. If you have any further questions or need additional learning materials, feel free to reach out. Your feedback is highly appreciated!
Joyce Kihn MD –
The training was fantastic! I learned so much about thermal management using PCMs. What were the specific temperatures when the phase change material started to melt and when it was fully liquid?
MR CFD Support –
In this CFD simulation, the phase change material starts melting at a solidus temperature of 307 K and becomes fully liquid at the liquidus temperature of 309 K as detailed in the provided simulation data.
Prof. Alena King –
The training product for Battery Cooling by PCM was superb! It helped me understand the thermal management complexities involved in lithium batteries using PCM. The simulation’s detailed approach allowed me to see the effectiveness of PCM layers in dissipating heat. Great job!
MR CFD Support –
Thank you for the positive feedback on our Battery Cooling by PCM training product. We are thrilled to hear that it effectively conveyed the cooling process using phase change materials and helped enhance your understanding of thermal management in lithium batteries.