Non-Newtonian Flow Between 2 Concentric Cylinders, Eulerian, ANSYS Fluent
$120.00 $60.00 Student Discount
The present problem simulates a non-Newton two-phase flow between two concentric cylinders using ANSYS Fluent software.
Click on Add To Cart and obtain the Geometry file, Mesh file, and a Comprehensive ANSYS Fluent Training Video.To Order Your Project or benefit from a CFD consultation, contact our experts via email (info@mr-cfd.com), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via info@mr-cfd.com after you buy the product.
Description
Non-Newtonian Flow Project Description
The present problem simulates a non-Newton two-phase flow between two concentric cylinders using ANSYS Fluent software. Fluids are divided into two categories in terms of viscosity: Newtonian and non-Newtonian fluids. Viscosity is a parametric fluid that indicates the degree of resistance of that fluid to flow. Newtonian fluids are fluids that follow Newton’s law of viscosity (shear stress in a Newtonian fluid changes linearly with strain rate) and also their viscosity depends only on the temperature and pressure of the fluid, and by applying a force to them in a constant temperature and pressure, their viscosity does not change.
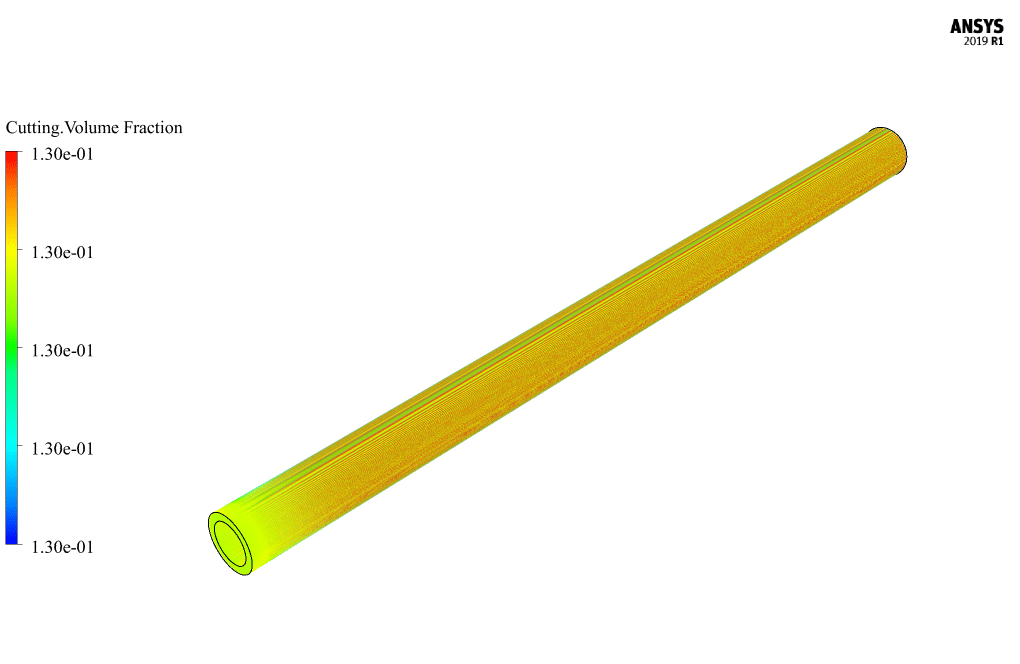
Non-Newtonian fluids, on the other hand, are fluids that do not follow Newton’s law of fluids, and their viscosity changes with the application of force. In this simulation, a two-phase flow is defined using the Eulerian model, the base fluid of which is a non-Newtonian fluid with a soluble fluid flowing through it. The base fluid has a density of 998.2 kg.m-3 and its viscosity is defined as non-Newtonian, which is non-Newtonian-power-law. The relation to the non-Newtonian viscosity value is as follows; So that k is equal to the criterion for measuring the average viscosity of the fluid and n is the criterion for the deviation of the fluid from the Newtonian state.
In this simulation, k is defined as 0.021 and n is defined as 0.75, and the minimum and maximum viscosity are 0.0001 kg.m-1.s-1 and 2000 kg.m-1.s-1, respectively. The soluble fluid in non-Newtonian fluid also has a density equal to 2000 kg.m-3 and a viscosity equal to 0.00111 kg.m-1.s-1.
Geometry & Mesh
The present model is designed in three dimensions using Design Modeler software. The model is a cylindrical channel with a length of 1 m and an inner diameter of 0.0225 m and an outer diameter of 0.03125 m.
We carry out the model’s meshing using ANSYS Meshing software. The mesh type is structured. The element number is 1396224. The following figure shows the mesh.
Non-Newtonian Flow CFD Simulation
We consider several assumptions to simulate the present model:
- We perform a pressure-based solver.
- The simulation is steady.
- The gravity effect on the fluid is ignored.
The following table represents a summary of the defining steps of the problem and its solution:
| Models (Non-Newtonian) |
||
| Viscous | k-epsilon | |
| k-epsilon model | standard | |
| near wall treatment | standard wall functions | |
| Multiphase Model | Eulerian | |
| number of eulerian phases | 2 | |
| formulation | implicit | |
| Boundary conditions (Non-Newtonian) |
||
| Inlet | Velocity Inlet | |
| gauge pressure | 0 Pascal | |
| velocity magnitude | 1.3566 m.s-1 | |
| volume fraction – primary phase | 0.87 | |
| volume fraction – secondary phase | 0.13 | |
| Outlet | Pressure Outlet | |
| gauge pressure | 0 pascal | |
| Inner wall | wall motion | Rotating wall (100 rpm) |
| Outer wall | wall motion | stationary wall |
| Methods (Non-Newtonian) |
||
| Pressure-Velocity Coupling | Coupled | |
| Pressure | PRESTO | |
| momentum | first order upwind | |
| turbulent kinetic energy | first order upwind | |
| turbulent dissipation rate | first order upwind | |
| volume fraction | first order upwind | |
| Initialization (Non-Newtonian) |
||
| Initialization methods | Standard | |
| gauge pressure | 0 Pascal | |
| velocity (x,y,z) | 0 m.s-1 | |
| volume fraction – primary | 1 | |
| volume fraction – secondary | 0 | |
Results & Discussions
At the end of the solution process, two-dimensional and three-dimensional contours related to pressure, velocity, volume fraction of non-Newtonian base fluid and volume fraction of soluble fluid were obtained.

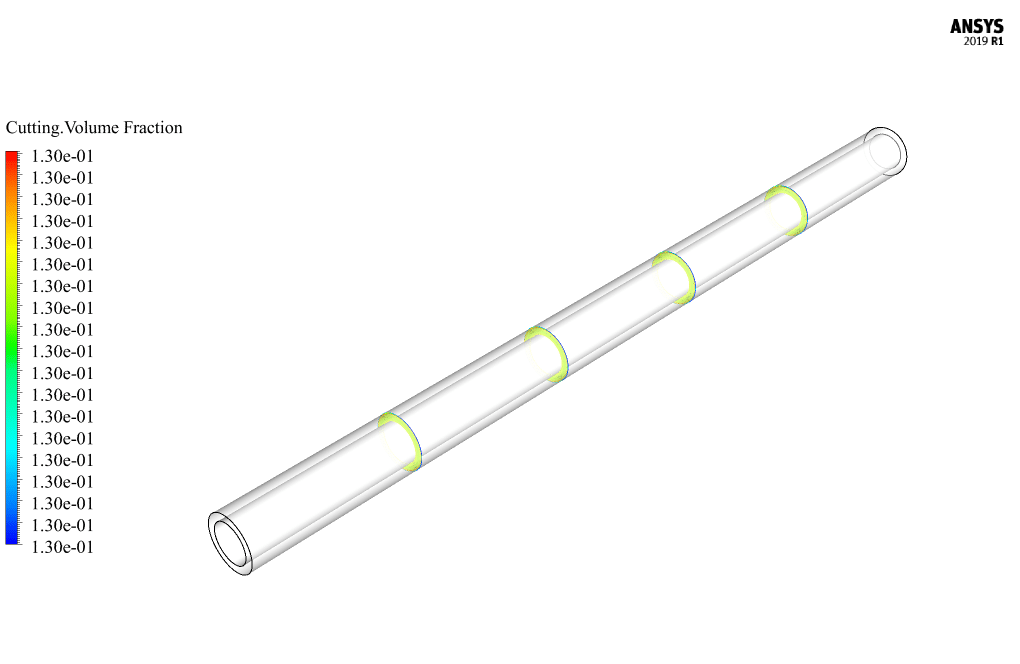
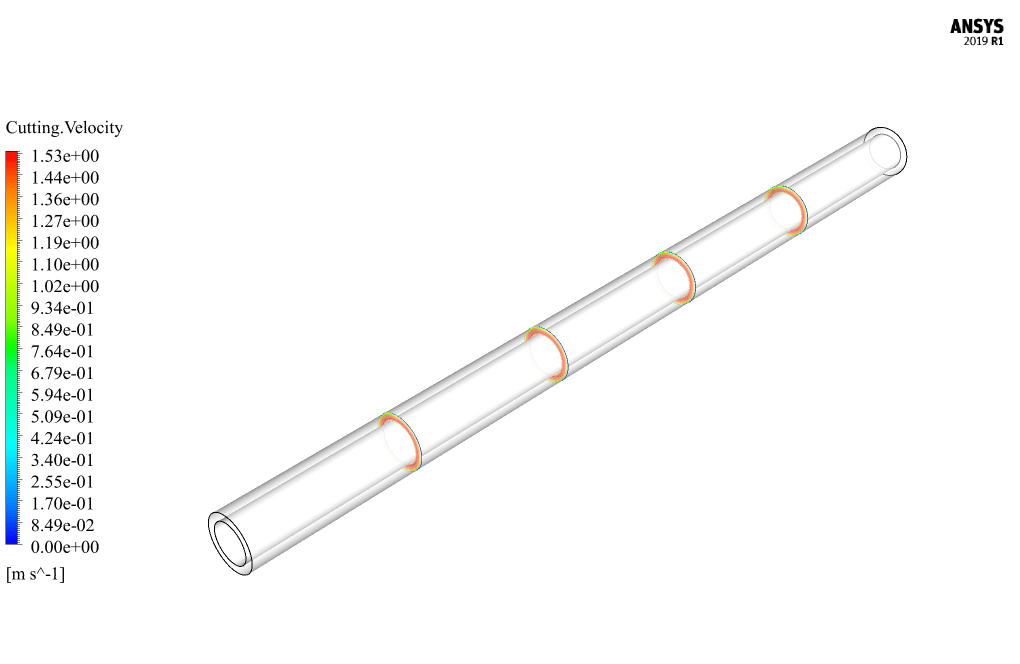

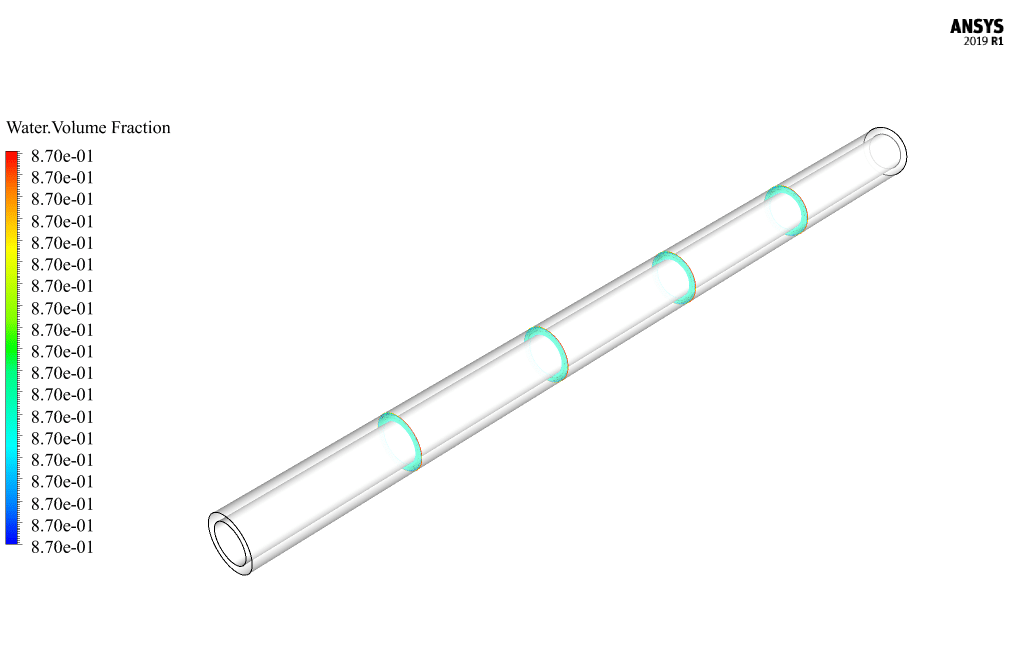
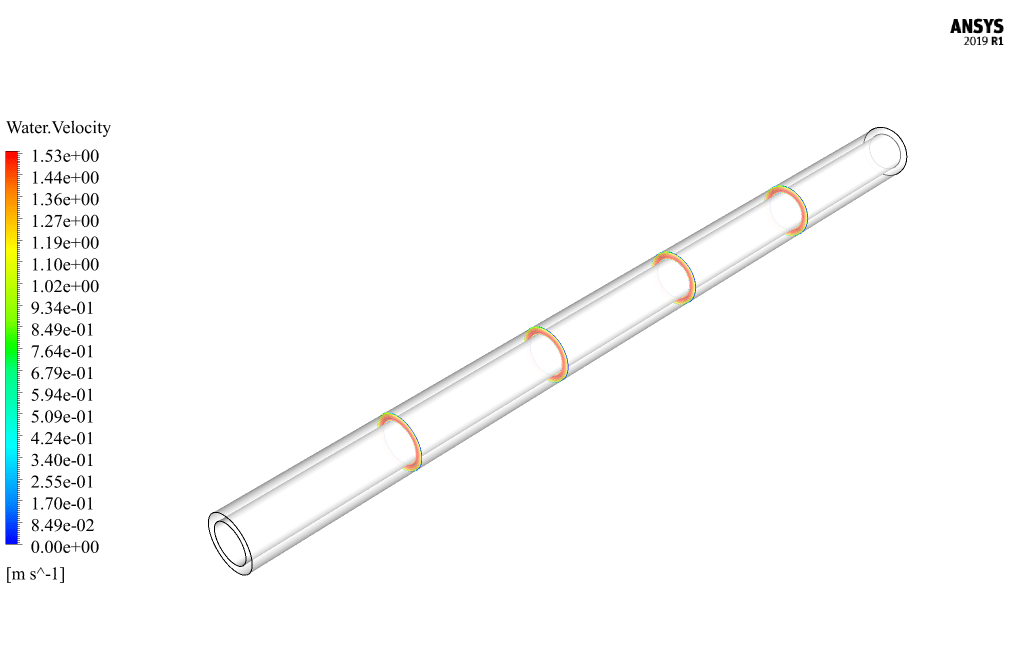

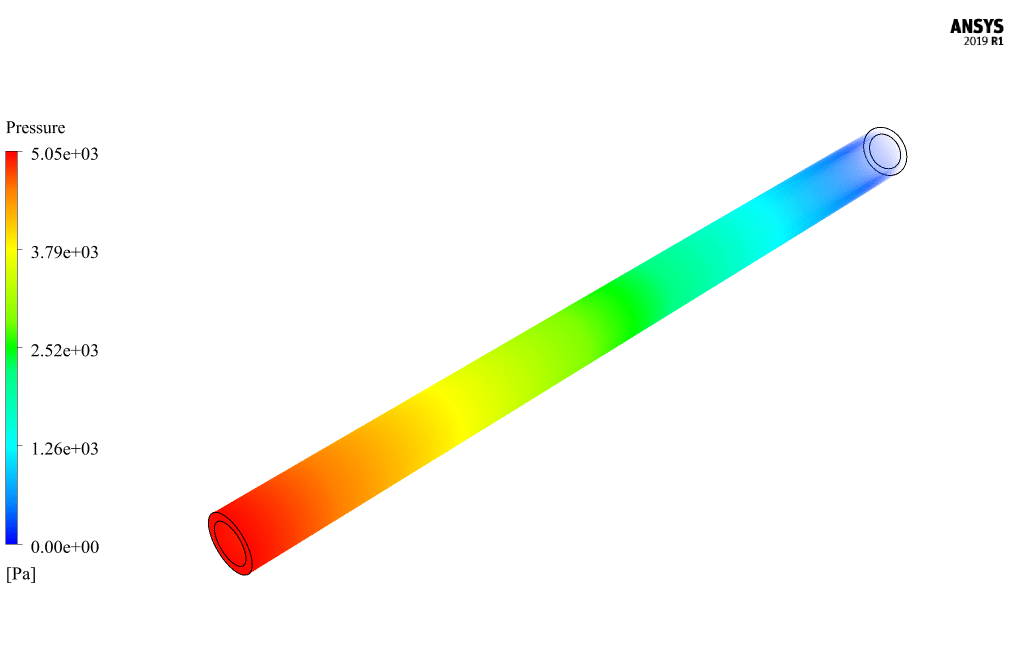


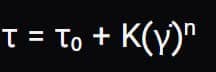





Toni Stokes –
I just wanted to express how impressed I was with the Non-Newtonian Flow Between 2 Concentric Cylinders simulation. The level of detail in the set-up and the comprehensive results provided deep insights into the fluid dynamics involved. Great work on illustrating the non-Newtonian behavior with clarity!
MR CFD Support –
Thank you so much for your kind words! We are pleased to hear that you found the simulation on Non-Newtonian Flow Between 2 Concentric Cylinders insightful and that it met your expectations. We strive to provide detailed and clear analyses, and your feedback validates our efforts. If you need further assistance or have more questions, don’t hesitate to reach out.
Jacky Streich –
I’m quite impressed with the simulation handling of non-Newtonian fluid dynamics. The explicit detail in setting up the Eulerian model for the two-phase flow, including the attention to the non-Newtonian fluid characterizations (parameter k for viscosity measurement and n for deviation from the Newtonian state), showcases a robust analysis. The structured mesh with over a million elements outlines a rigorous approach to capturing the fluid interactions accurately. However, can you elaborate how the simulation results reflect on the applicative use of non-Newtonian fluids for industrial processes?
MR CFD Support –
Thank you for your kind words about the simulation and the specific aspects of the Eulerian model and the non-Newtonian fluid characterizations. The richly detailed and precise simulation provides invaluable insight into the behavior of non-Newtonian fluids under different flow conditions. While the simulation was comprehensive, it didn’t address direct applicative use, but generally, understanding such flow characterizations is essential for applications involving complex fluids, such as in the food, cosmetic, and polymer industries. By understanding the detailed fluid dynamics from such simulations, engineers can better design equipment and processes that handle or utilize non-Newtonian fluids.
Edna Moore –
I found the explanation of non-Newtonian fluids particularly insightful! Great to see the intricate details involving viscosity and how it was adapted in the simulation.
MR CFD Support –
Thank you so much for your kind words! We’re thrilled to hear that our simulation has provided you with a deeper understanding of non-Newtonian fluids. It’s always our goal to deliver thorough and insightful analyses, and we’re glad this was reflected in our work. If you have any more questions or need further assistance in the future, feel free to reach out!
Katelynn DuBuque –
The simulation setup seems very detailed. Was experimental or field data used to validate the computational results of the non-Newtonian two-phase flow between the cylinders?
MR CFD Support –
The information provided does not indicate whether experimental or field data were used for validation. Verification and validation are indeed critical steps, but the provided data focuses on the simulation setup and results without mentioning validation practices.
Mr. Wellington Hills –
Which parameter determines the degree of deviation from the Newtonian state in this simulation?
MR CFD Support –
In this simulation, the parameter ‘n’, which is a part of the power-law model for non-Newtonian fluids, determines the degree of deviation from the Newtonian state.
Dr. Justen Medhurst Jr. –
Could you please elaborate on how the gravitational effects were omitted in the simulation and what impact this might have on the accuracy in an actual scenario?
MR CFD Support –
In this simulation, the gravitational effects were omitted to simplify the problem and focus solely on the non-Newtonian fluid behavior between the concentric cylinders. In reality, omitting gravity could impact flow patterns, especially if buoyancy effects are significant. However, the assumption is made here that for the specific case of steady, concentric flow, gravity would have minimal impact. The accuracy of this assumption would depend on the practical application and the density differential that gravity would influence.
Alverta Harris –
Just finished reviewing the Non-Newtonian flow simulation; I must applaud the in-depth analysis and stunning visuals provided. The explanations were quite insightful, and the results section really highlighted the crucial findings effectively.
MR CFD Support –
Thank you for your positive feedback! We’re thrilled to hear that you found the simulation analysis to be comprehensive and the visuals engaging. At MR CFD, we strive to provide quality educational content and are glad it was beneficial to you.
Johnny Mueller DDS –
What difference did you find between Newtonian and non-Newtonian fluid behaviors in this simulation, especially regarding their responses to the applied force?
MR CFD Support –
The primary difference seen in the simulation between Newtonian and non-Newtonian fluids is their behavior when force is applied. For the non-Newtonian fluid with a power-law behavior, its viscosity changes with force application with a demonstrable variance denoted by the power-law constants k and n. Unlike Newtonian fluids which sustain a constant viscosity at a fixed temperature and pressure, the non-Newtonian fluid in this simulation exhibited a change in viscosity with applied stress.
Myra Stanton –
Does the non-Newtonian fluid’s behavior impact the mixing process of the two fluids?
MR CFD Support –
Yes, the non-Newtonian behavior of the fluid can significantly impact the mixing process. Its variable viscosity means that it responds differently to shear rates than a Newtonian fluid would, which affects the overall flow and mixing patterns between the two fluids in the concentric cylinders.
Lauryn Keeling –
The learning material is so comprehensive and well-presented. The structured mesh detailing and in-depth explanation of Non-Newtonian flow physics enhanced my understanding significantly.
MR CFD Support –
Thank you for your kind words! We strive to provide well-structured and detailed learning materials, and we’re glad to hear that the product about non-Newtonian flow met your expectations. If there’s anything more you want to learn about, feel free to explore our other offerings.
Mr. Russ Beier –
What is the challenge of simulating non-Newtonian fluids compared to Newtonian fluids?
MR CFD Support –
The challenge of simulating non-Newtonian fluids, as opposed to Newtonian fluids, lies in the complexity of modeling their viscosity. Non-Newtonian fluids do not have constant viscosity, which means their flow characteristics cannot be described using a simple linear relationship between shear stress and strain rate as with Newtonian fluids. Instead, their viscosity can change under varying shear rates or deformations, making the determination of the flow field more complex and often requiring advanced rheological models and numerical methods.
Mr. Jaren Aufderhar PhD –
This product seems to have an in-depth approach to simulating non-Newtonian fluids. Can you tell me if the same methodology applied here for non-Newtonian fluids can be used for any type of non-Newtonian fluid in different geometries or setups?
MR CFD Support –
While the methodology employed in this simulation is designed for a non-Newtonian fluid using Eulerian multi-phase models, it is tailored to the specific parameters and the cylindrical geometry of the problem at hand. The principles can often be extrapolated to different geometries and non-Newtonian fluids; however, adjustments to the simulation parameters, such as viscosity models, boundary conditions, and meshing, would certainly be required. These adjustments depend heavily on the fluid properties and system characteristics of the new geometry or setup in question.