Wet Steam for Condensation inside a Steam Ejector

Wet Steam CFD Simulation for Condensation inside a Steam Ejector, ANSYS Fluent

The present problem simulates the process of steam condensation inside an ejector using ANSYS Fluent software.

The system in which the occurrence of the condensation process is investigated belongs to an ejector. An ejector is a mechanical device that uses an actuator fluid to suck in the secondary material.

Finally, the two actuator fluids and the suction substance are mixed and removed from the system. Ejectors have two main functions, including vacuuming and suctioning gases and mixing fluids.

The ejector structure is in the form of a convergent-divergent tube which, by entering the driving fluid into it and passing through the converging part of the nozzle, according to the continuity equation, causes the velocity of the passing fluid to increase by reducing the cross-sectional area of ​​the flow; In fact, the potential energy of the fluid is converted into kinetic energy.

Then, according to Bernoulli’s law, the fluid pressure decreases with increasing velocity and, consequently, the kinetic energy of the fluid.

The current model is designed in two dimensions using Design Modeler software. The model corresponds to an ejector’s two-dimensional plane, so it has a length of 0.411 m, an exit with a width of 0.02 m, a first entrance with a width of 0.0038 m, and a second entrance with a width of 0.0165 m.

Also, the lower edge of the model is defined as an axis; That is, the two-dimensional geometry of the model can be rotated around this axis and turned into a three-dimensional structure.

In fact, due to the perfectly symmetrical structure of the geometry of this ejector and to reduce the computational cost, the geometry is defined in two dimensions.

The meshing has been done using ANSYS Meshing software. The mesh type is structured, and the number of production cells is equal to 25984.

Wet Steam Methodology

When the Wet Steam multiphase model is used, two sets of transport equations are solved: the mass fraction of the condensed liquid phase and the number or concentration of droplets per unit volume.

This phase change model involves forming liquid droplets during a homogeneous non-equilibrium condensation process and is based on the classical non-isothermal nucleation theory.

This model causes the superheated dry steam to cool first after a rapid expansion of the steam and then to form a core, consisting of a two-phase mixture of saturated steam and liquid droplets called wet steam. Also, we perform a density-based solver.

Wet Steam Conclusion

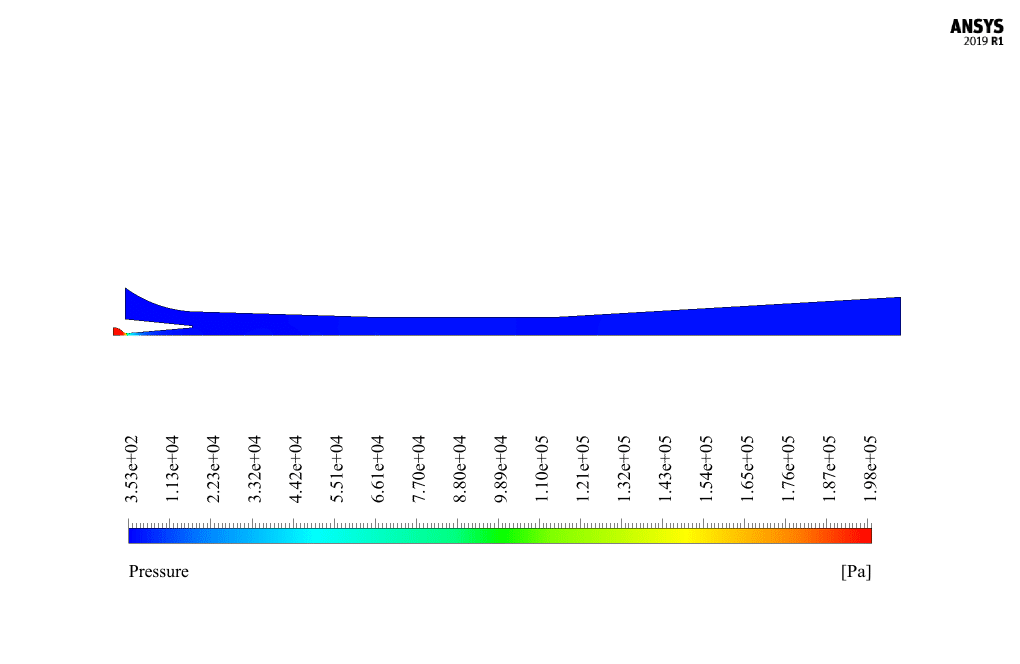
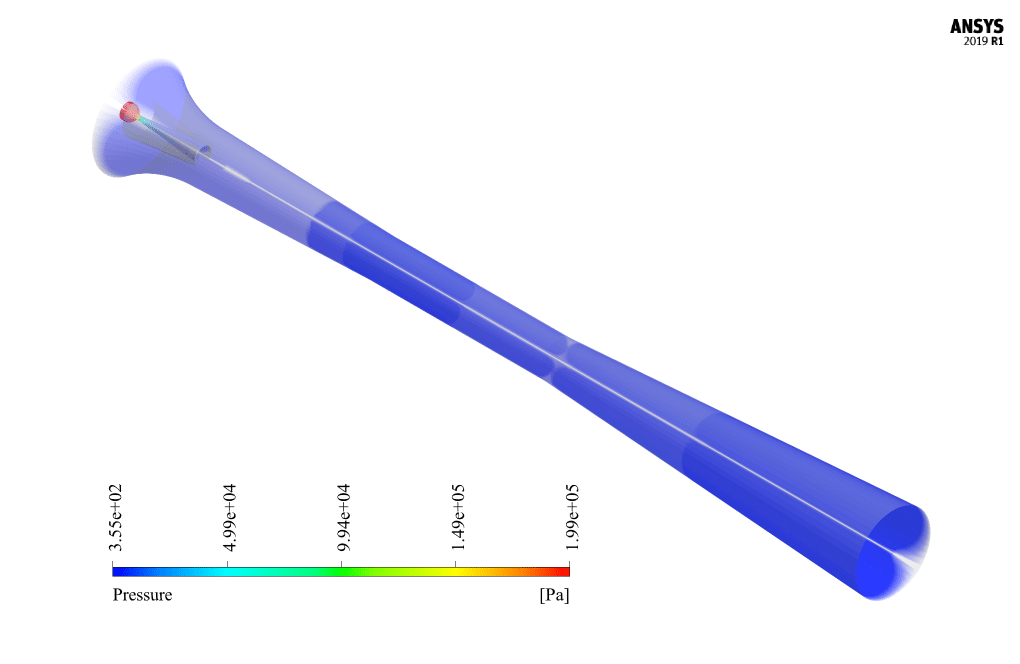
The resulting pressure drop creates a compressive vacuum inside the ejector, which causes the secondary material to suck into the ejector. The primary stimulation fluid and the suction secondary material are mixed and compressed in the diffuser section.

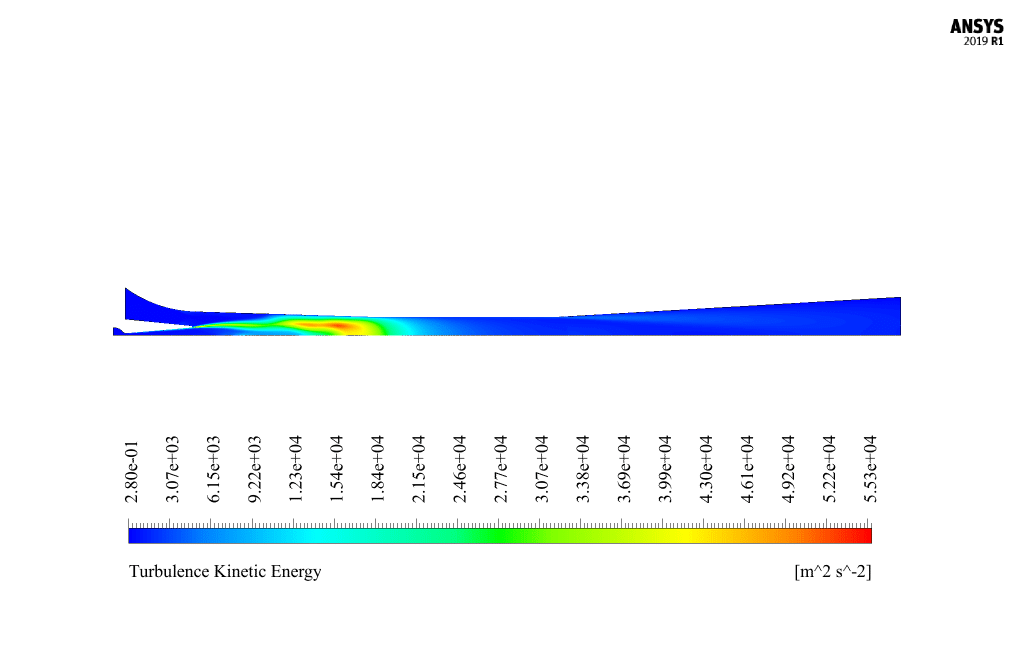
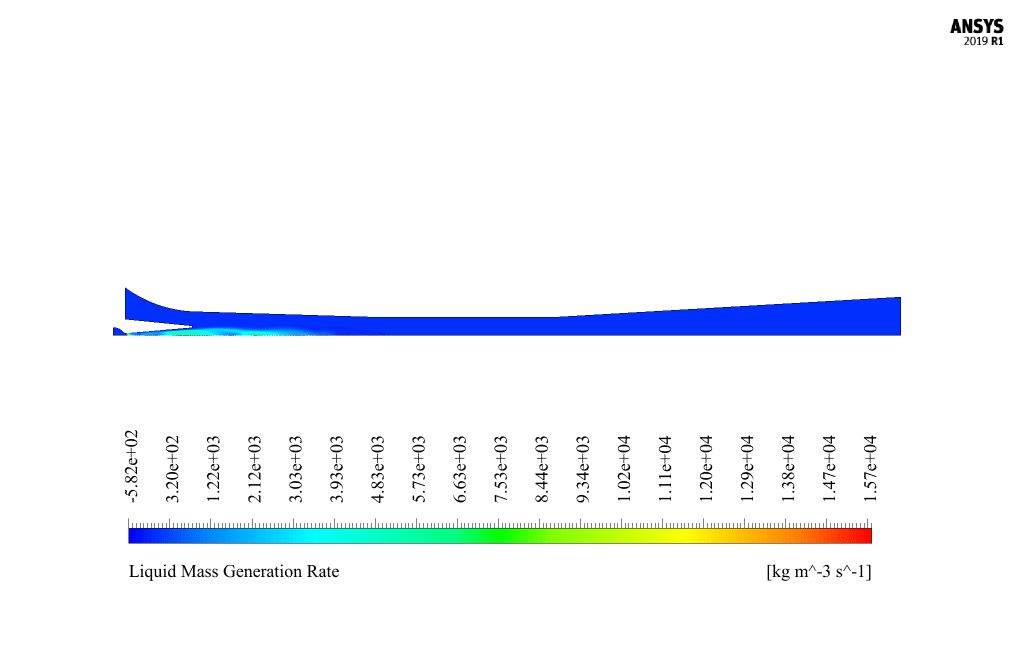
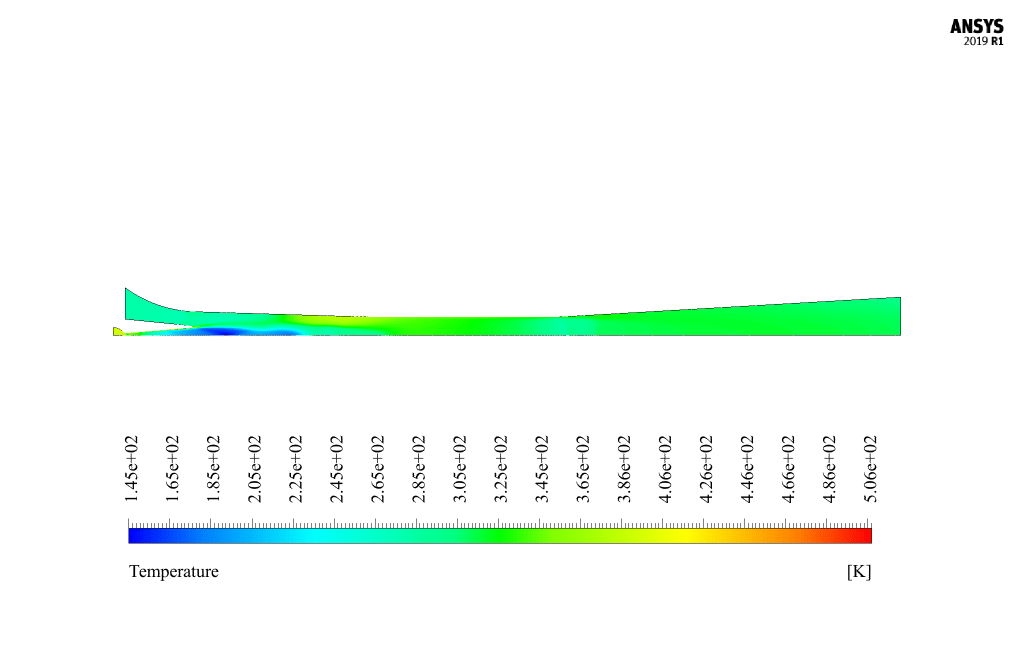
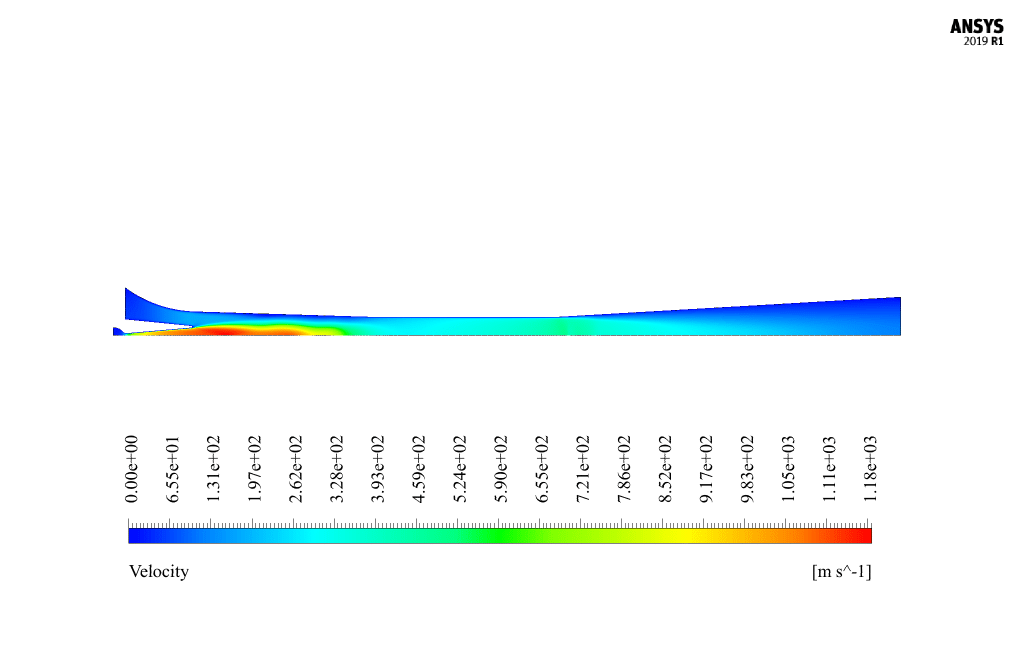
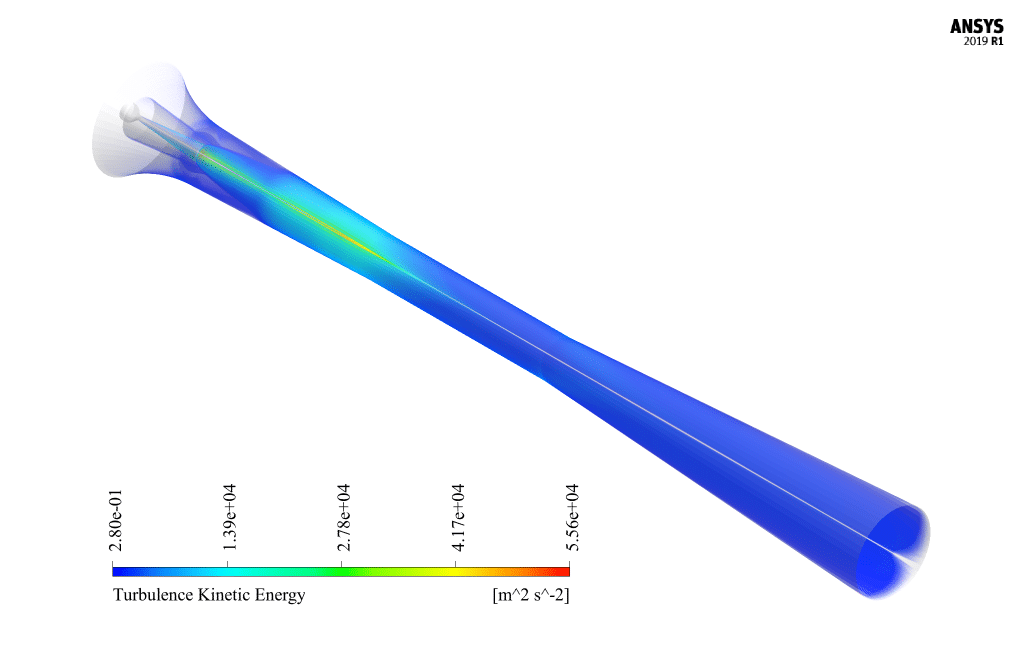
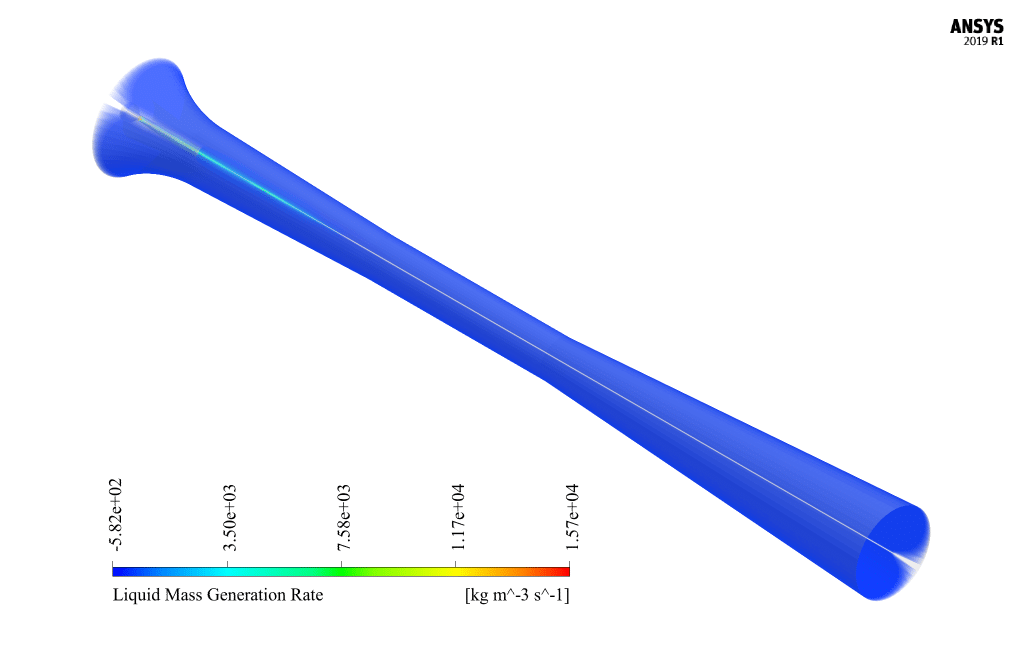
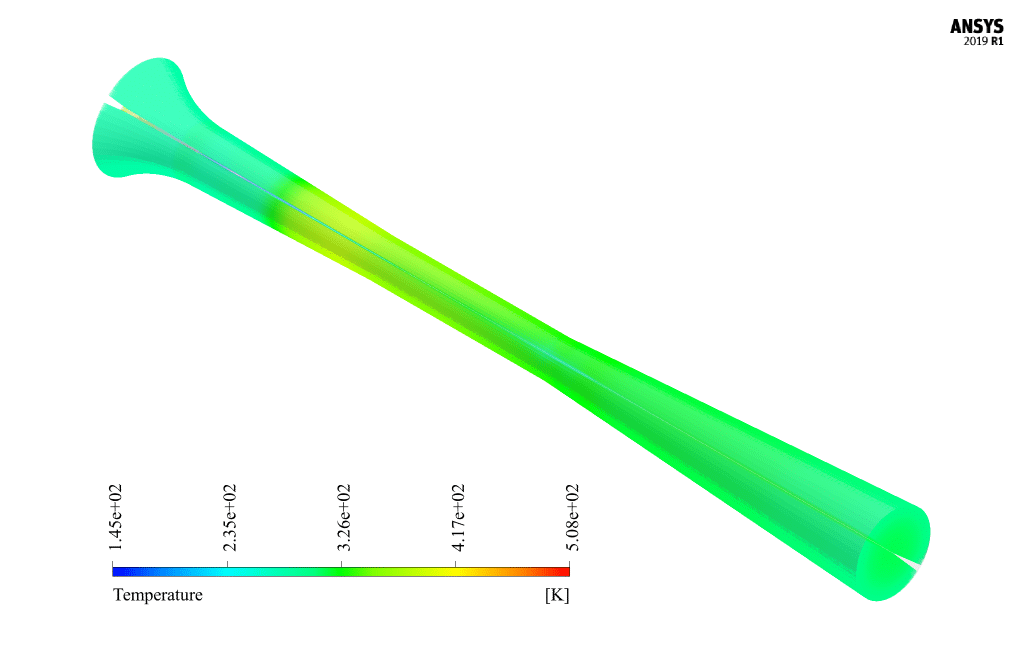
At the end of the solution process, we obtain two-dimensional contours related to pressure, velocity, temperature, turbulent kinetic energy, and the rate of mass production of liquid vapor (same as the density rate).

It is also possible to obtain a three-dimensional contour of these parameters by rotating this two-dimensional contour around the central axis. The liquid mass generation rate is one of the most important results and can be analyzed.