Porous Chamber Heat Transfer CFD Simulation, Tutorial
$80.00 Student Discount
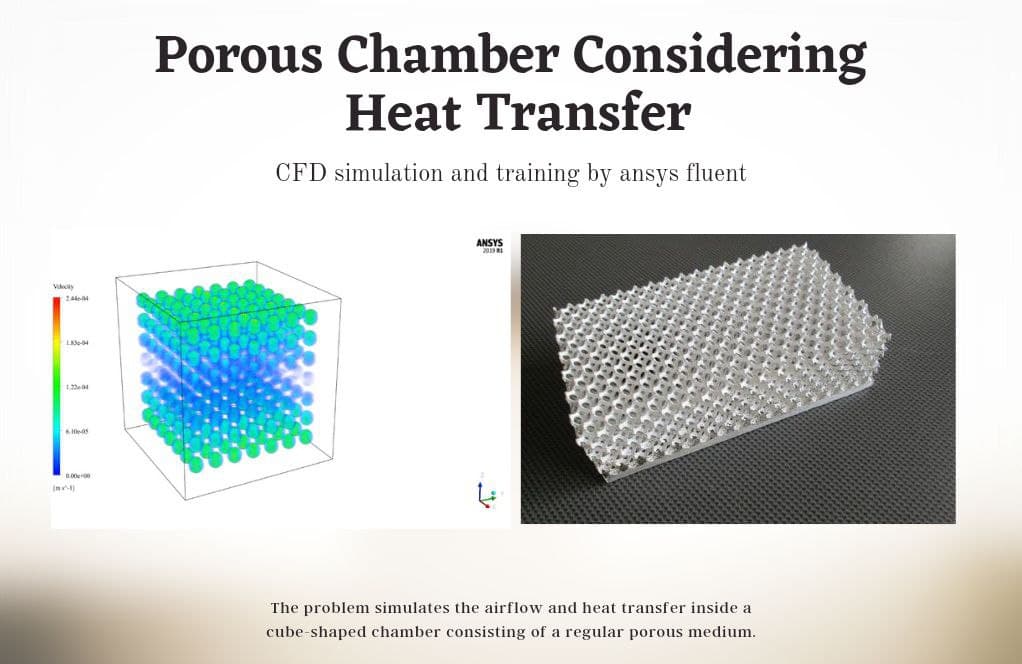
The problem simulates the airflow and heat transfer inside a cube-shaped chamber consisting of a regular porous medium.
Click on Add To Cart and obtain the Geometry file, Mesh file, and a Comprehensive ANSYS Fluent Training Video.To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Porous Chamber Considering Heat Transfer, ANSYS Fluent CFD Simulation Training
The problem simulates the airflow and heat transfer inside a cube-shaped chamber consisting of a regular porous medium by ANSYS Fluent software. The porous medium used in this chamber is in the form of rows and columns of several aluminum balls, the number of which is 343. These aluminum balls have a density of 2719 kg.m-3, a specific heat capacity of 871 j.kg-1.K-1, and thermal conductivity of 0.5 W.m-1.K-1.
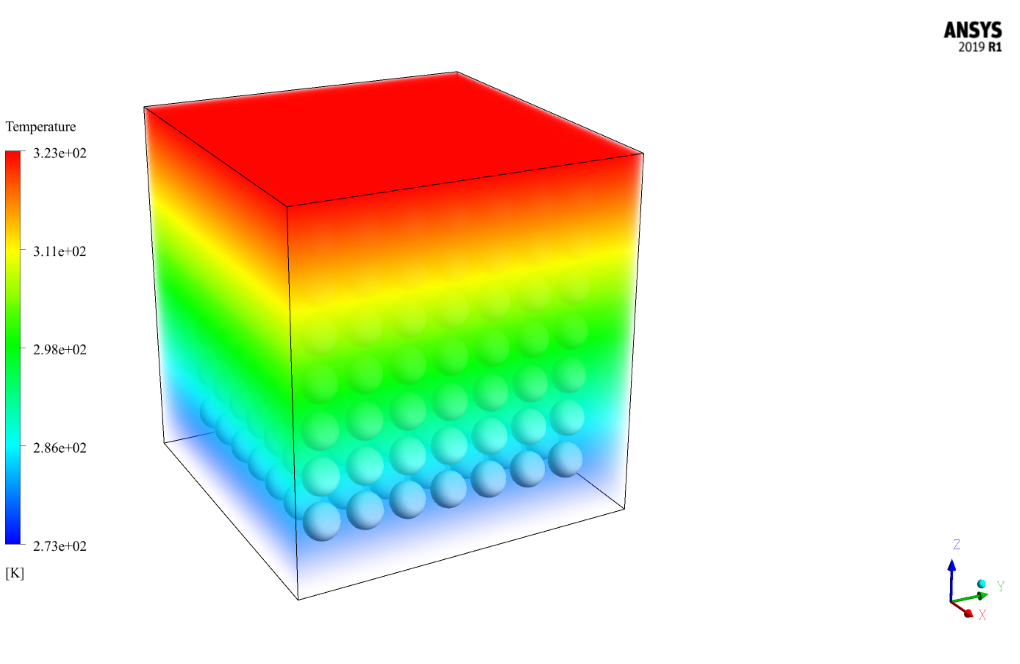
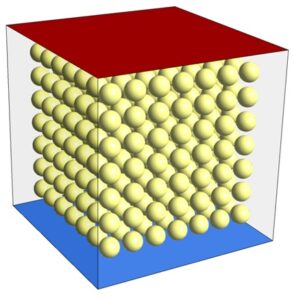
The fluid in this chamber is air and there is no special air inlet and outlet for the chamber. The main purpose of this study is to investigate changes in air temperature inside the chamber under the influence of these items as a porous medium. In fact, the upper surface of the chamber has a constant temperature of 323 K and the lower surface has a constant temperature of 273 K, and the side walls are also insulated.
Porous Chamber Geometry & Mesh
The present model is three-dimensional and is drawn using the ِ Design Modeler software. The present model is related to the chamber, which has seven spheres as a porous medium in three different directions. The total number of these spheres is 343. The figure below shows a view of the geometry.
The meshing of the model has been done using ANSYS Meshing software and the mesh type is unstructured. The element number is 3451362. The figure below shows a view of the mesh.
Heat Transfer in a Porous Chamber CFD Simulation
To simulate the present model, several assumptions are considered:
- The solver is a pressure-based perspective.
- The present simulation is steady.
- The gravity of -9.81 m.s-2 is considered.
A summary of the steps for defining a problem and defining its solution is given in the following table:
| (Porous) | Models | |
| Viscous model | k-epsilon | |
| k-epsilon model | standard | |
| near-wall treatment | standard wall function | |
| Energy | on | |
| (Porous) | Boundary conditions | |
| down wall | Wall | |
| wall motion | stationary wall | |
| temperature | 273 K | |
| up wall | Wall | |
| wall motion | stationary wall | |
| temperature | 353 K | |
| sides walls | ||
| wall motion | stationary wall | |
| heat flux | 0 W.m-2 | |
| (Porous) | Solution Methods | |
| Pressure-velocity coupling | Coupled | |
| Spatial discretization | pressure | standard |
| density | second-order upwind | |
| momentum | second-order upwind | |
| energy | second-order upwind | |
| turbulent kinetic energy | first-order upwind | |
| turbulent dissipation rate | first-order upwind | |
| (Porous) | Initialization | |
| Initialization method | Standard | |
| gauge pressure | 0 Pa | |
| velocity (x,y,z) | 0 m.s-1 | |
| temperature | 298 K |
Results
At the end of the solution process, two-dimensional and three-dimensional contours of velocity, pressure, and temperature, as well as two-dimensional and three-dimensional velocity vectors are obtained.






Bennett Fritsch –
Is it possible to use this simulation to represent heat transfer in porous media when different fluid properties are involved?
MR CFD Support –
Yes, the simulation can be adjusted to model heat transfer in porous media with a variety of fluid properties. This includes different types of fluids and their specific properties, such as viscosity and thermal conductivity.
Brando Hand –
I want to know how the simulation handles the impact of the porous medium’s material properties on heat transfer?
MR CFD Support –
The simulation takes into account the specific material properties of the porous medium, such as thermal conductivity and specific heat capacity. These properties can be set based on the specific material being simulated.
Ian Sauer Jr. –
Will the aluminum balls’ spacing or the size have a significant impact on the heat transfer within the chamber? Is there any comparison in the results section that helps to understand the effect of these parameters?
MR CFD Support –
The spacing between and size of the aluminum balls absolutely influence the heat transfer characteristics within the chamber. Changing these parameters can alter the flow and thermal fields significantly. Although the review doesn’t mention comparative results regarding different spacings or sizes, such an analysis would typically be included in a full CFD study to understand their effects comprehensively.
Zoey Cormier II –
The aluminum balls in the porous medium—do they act solely as a passive component for heat transfer, or do they have any mechanical interaction with the airflow as well?
MR CFD Support –
In the simulation, the aluminum balls primarily enhance heat transfer due to their material properties. While they influence the airflow by creating additional surface area through which air must move, thereby impacting flow patterns, their mechanical interaction—such as causing pressure drop or flow redirection—is also accounted for by their placement within the porous medium, influencing overall airflow behavior within the chamber.
Perry Rath –
Absolutely fascinating tutorial on porous media and heat transfer! Understanding the interaction of airflow with a porous medium and how temperature gradients affect the airflow was enlightening. The meticulous detail put into the simulation setup, especially defining the boundary conditions and the step-by-step process of defining the problem, highlights the high educational value of the product. Thank you for this comprehensive tutorial; it certainly broadens my knowledge in applying CFD to such scenarios.
MR CFD Support –
We’re thrilled that you found the porous chamber heat transfer simulation tutorial educational and valuable. It is our goal to provide comprehensive learning tools that expand our customers’ knowledge and application of CFD. Thank you for your positive feedback, and we are glad to have contributed to your learning experience.
Lavon Cormier –
How does the simulation account for the porosity of the medium?
MR CFD Support –
The simulation takes into account the porosity of the medium by adjusting the parameters such as permeability and inertial resistance. These parameters can be set based on the specific properties of the porous medium being simulated.
Micah Wisoky –
Can this simulation be used to model heat transfer in different types of porous media?
MR CFD Support –
Absolutely, the simulation can be adjusted to model heat transfer in a variety of porous media. This includes different types of materials, porosities, and permeabilities.
Dorcas Gibson –
The tutorial was extremely informative, particularly the step-by-step setup details. However, I’m a bit confused about the initialization method. Could you explain why the standard initialization method was chosen over others and how this affects the simulation results?
MR CFD Support –
The Standard initialization method is selected often for setting a starting solution based on the defined boundary conditions and estimations within the domain, providing a smooth start to iterating the solution. It affects the convergence behavior and can help in achieving a stable solution faster. It doesn’t influence the final steady-state solution, provided the simulation is run to convergence.
Ava Little –
The simulation training was articulate and comprehensive. But I’m curious about one part. How does your training handle the setup and explanation of porous zone parameters and their impact on the simulation outcomes?
MR CFD Support –
In our simulation training, we thoroughly address the setup of porous zone parameters such as porosity, permeability, and inertial resistance factors. These parameters significantly influence the flow and heat transfer within the porous medium. Our training covers how these parameters are derived, applied within the ANSYS Fluent software, and how they affect the predictions of temperature and fluid velocities, ensuring a deep understanding of their impact on simulation outcomes.
Mr. Diego DuBuque V –
Can this simulation be used to evaluate the performance of different types of heat exchangers?
MR CFD Support –
Yes, the simulation can be used to evaluate the performance of different types of heat exchangers. By accurately simulating heat transfer in the porous medium, it can help identify the most effective heat exchanger designs.
Allan Rutherford –
The training material discuss the results of the simulation. Could hyperbolic models have been more appropriate for convective heat transfer in the porous media instead of using a standard k-epsilon model?
MR CFD Support –
In the simulation of heat transfer in porous media, the k-epsilon model is an option for representing turbulence in the fluid flow. However, for convective heat transfer, one might argue for the potential use of a hyperbolic heat conduction model if the problem involves high-speed or rapidly changing conditions. This would depend on the specifics of the simulated scenario. The training provided focuses on steady-state conditions, where the k-epsilon model with standard wall functions is typically acceptable. If rapid transient effects were significant, exploring a hyperbolic model for the tutorial could be feasible, but in the context provided, the chosen models are sufficient as they are commonly used for steady porous flow simulations.
Mr. Jeffrey Schuppe –
The training was thorough! The steps explained for setting up heat transfer in a porous medium were clear and easy to follow—setting a solid foundation for my project on similar scenarios. Great job on outlining the discretization methods; it helped me better understand the solution strategy for refined results. Keep up with the fantastic educational content!
MR CFD Support –
Thank you so much for your kind words! It’s fantastic to hear that the training on heat transfer in porous media was helpful for your project and that the simulation steps were clear to you. If you ever have more questions or need further assistance on your learning path, don’t hesitate to reach out. We’re thrilled to contribute to your solid foundation in CFD!
Caleb Bergnaum –
This training seems quite comprehensive. Have you encountered any issues with convergence due to the complexity of the porous media interaction with the airflow, or was the process smooth with the settings provided?
MR CFD Support –
We are thrilled to hear your positive feedback! Rest assured, the tutorial has been designed to address potential convergence issues by fine-tuning solver settings and providing best practices for dealing with complex porous media simulations. Given the stringent boundary conditions and detailed setup guidelines provided, the convergence process should generally be smooth, especially with the second-order upwind discretization techniques adopted for most physics apart from the first-order treatment for turbulence models to initiate a more stable solution. Feel free to explore the tutorial and the intricate interactions between the porous media and airflow!
Lue Kreiger Jr. –
What was the rationale behind choosing the specific materials and properties for the porous medium I’m this study?
MR CFD Support –
The specific materials and properties like the aluminum balls with a density of 2719 kg.m-3, a specific heat capacity of 871 j.kg-1.K-1, and thermal conductivity of 0.5 W.m-1.K-1 represent a standard set used in such simulations to effectively simulate heat transfer within a porous chamber. The properties are chosen for their ability to approximate a realistic thermal response when subject to various temperatures.
Keeley Williamson –
Thank you for the highly detailed tutorial on simulating heat transfer in a porous chamber! It was especially helpful to see how the aluminum balls’ properties and arrangement affect airflow and heat distribution. The constant temperatures set for the upper and lower surfaces provided a clear temperature gradient, making it easier to understand heat transfer in the system.
MR CFD Support –
We’re thrilled to hear that our tutorial on the heat transfer simulation in a porous chamber was helpful to you! Understanding the intricacies of heat and airflow in complex systems is essential for accurate CFD analyses, and we’re glad we could assist in clarifying these concepts. Should you have any further questions or need more assistance on this topic or any others, please don’t hesitate to get in touch. Thank you for your positive feedback!
Ms. Zena Raynor Jr. –
I’m impressed by the attention to detail in this project. It’s clear from the elaborate setup that a thorough investigation of heat transfer in porous media was conducted, especially considering the effect of aluminum balls on airflow in the chamber. Well done on going the extra length to illustrate real-world applications!
MR CFD Support –
Thank you for your thoughtful review and kind words! We are delighted to know that the Porous Chamber Heat Transfer CFD Simulation tutorial met your expectations and was beneficial for your understanding of heat transfer in porous media. We are always here to support passionate learners like you. If you ever have any questions or need further clarification on our products, feel free to reach out.
Prof. Vincenzo Friesen IV –
I’ve completed the tutorial and was amazed by the temperature contours and the airflow pattern within the porous chamber. It was fascinating to see how heat transfer is simulated in such a system. Kudos to MR CFD Company for a well-structured and informative learning product. The step-by-step guide was particularly helpful.
MR CFD Support –
Thank you for your kind words! We’re thrilled to hear that you found the tutorial on ‘Porous Chamber Heat Transfer CFD Simulation’ informative and that the visual representation of heat transfer enhanced your learning experience. We strive to deliver clear and thorough instructions to assist our customers, and it’s rewarding to know that our efforts are making a difference. We appreciate you taking time to provide positive feedback!