Solar Still (3-D) by Species Transport Model, ANSYS Fluent CFD Simulation Training
$220.00 Student Discount
The present study investigates the performance of a solar-still thermal desalination unit.
Click on Add To Cart and obtain the Geometry file, Mesh file, and a Comprehensive ANSYS Fluent Training Video.To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Solar Still (3-D) by Species Transport Model
problem Description for Desalination
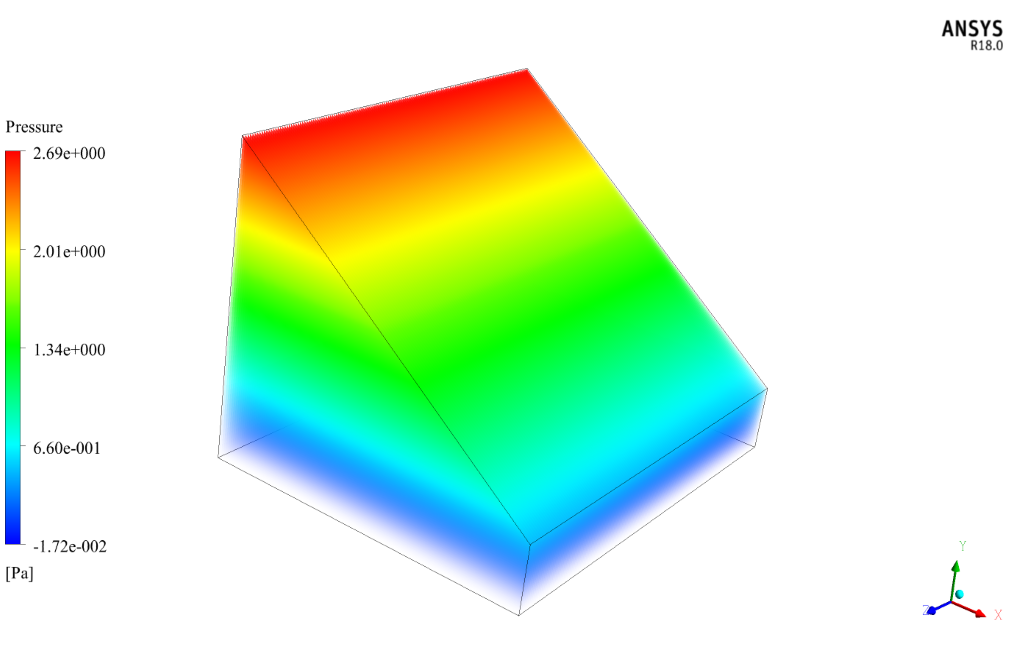
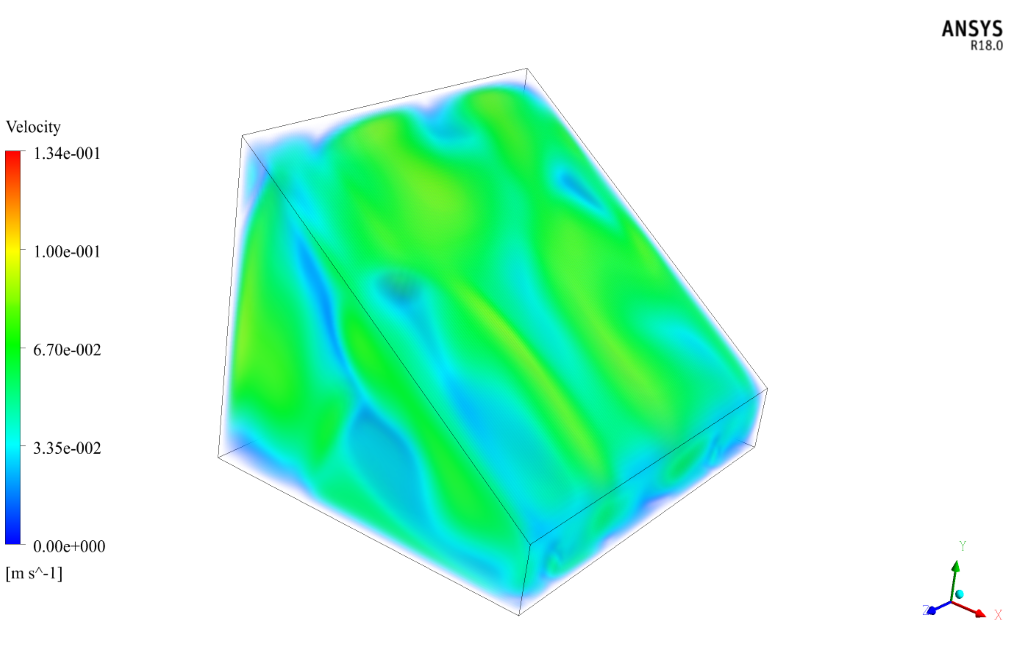
The present study investigates the performance of a solar-still thermal desalination unit by ANSYS Fluent software. The present model consists of a small chamber with a sloping glass surface at the top. The solar heat passes through the glass to the surface of the water in the enclosure and causes surface evaporation (applying a UDF for surface evaporation). The resulting vapor impact to the cold glass surface and undergo a distillation process. Pure water from hot vapor distillation moves down the slope of the glass plate and discharges as pure water.
To solve this problem, the Species Transport method is used. When using this method, saline water flow is not simulated in the device, unlike methods such as multiphase simulations that have much heavier computations. This assumes that there is a mixture of air and vapor inside the chamber interior. In fact, the simulation focuses solely on the amount of vapor produced in the system, and the purpose of the present study is to investigate the amount of vapor produced on the water surface and the cold surface of the sloping plate.
The Assumption for Solar Still CFD Simulation
There are several assumptions to simulate the present problem:
The simulation is Steady-State and the solver is Pressure-Based. The effect of the earth’s gravity on the flow is considered equal to 9.81 m.s-2 because in this problem the glass plate slope causes the downward movement of the distilled water.
Geometry and Mesh
The present 3-D model was designed by Design Modeler software. The geometry consists of a sloping glass surface at the top and a horizontal water plate at the bottom.
A structured mesh was performed using ANSYS Meshing software. The element number is 500,000.
Solar Still CFD Simulation
Here is a summary of the steps to define and solve the problem:
| Models | ||||
| Laminar | Viscous model | |||
| Species transport | Species | |||
| air and vapor | species | |||
| on | Energy | |||
| Boundary conditions for desalination | ||||
| wall | Walls type | |||
| 0 W.m-2 | heat flux | back, front, side walls | ||
| zero | diffusive flux for h2O | |||
| 343.95 K | temperature | ground walls | ||
| 1 | mass fractions for h2O | |||
| 338.05 K | temperature | glass walls | ||
| 1 | mass fractions for h2O | |||
| Solution Methods for solar still simulation | ||||
| Simple | Pressure-velocity coupling | |||
| PRESTO | pressure | Spatial discretization | ||
| first order upwind | momentum | |||
| first order upwind | energy | |||
| first order upwind | h2O | |||
| Initialization for Desalination simulation | ||||
| Standard | Initialization method | |||
| 341 K | temperature | |||
| 0 m.s-1 | velocity (x, y, z) | |||
Species Transport
This method assumes that there is a mixture of air and vapor inside the chamber interior and does not simulate distilled water flow. In fact, at the beginning of the simulation, the space inside the chamber is filled with air only; the bottom plane of the chamber is considered as the surface of the water, and since the water evaporates on the surface, it is assumed that the surface consists of vapor. It is also assumed that the sloping plate where the steam collides with, is composed of vapor only.
The equation governing the flow of gaseous species present in the simulation is as follows:
Species Transport
In the above equation, Yi represents the gas species present in the equation, which includes air and vapor in the present model. The first term on the left is equivalent to the time-dependent term (if unsteady) and the second term is the equivalent of the transport term. The first term is the equivalent of the diffusion term (including mass and thermal diffusion), the second term is the equivalent of the chemical reactions term (if any) and the third term is for heat sources (if any).
The two mass diffusivity and thermal diffusion coefficient parameters indicate mass diffusion and thermal diffusion, respectively. such that the mass diffusion coefficient is equal to the constant value of 2.88⨯10-5 m2.s-1 and the thermal diffusion coefficient is equivalent to the conductivity coefficient to specific heat capacity ratio, which is equal to 4.56754⨯10-5 kg.m-1.s-1.



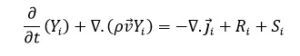



Emmy Mante –
It was great and perfect.
Dr. Craig Reinger IV –
How does the simulation handle the phase change from water to vapor?
MR CFD Support –
The simulation handles the phase change from water to vapor using the mass transfer model in ANSYS Fluent, which allows for accurate prediction of evaporation and condensation processes
Dr. Deshawn Haley –
Can the simulation be customized to fit specific requirements?
MR CFD Support –
Yes, at MR-CFD, we are open to contributions and can accommodate your desired simulations. Please feel free to reach out to us with your specific requirements.
Mr. Prince Lindgren –
MR-CFD was fluent and provided good content.
Dr. Mike Macejkovic –
Just finished the Solar Still CFD Simulation training, and it was fascinating to see how the species transport model could so effectively demonstrate the distillation process! The use cases for this are captivating.
MR CFD Support –
Thank you for your positive feedback! We’re thrilled to hear that you found the Solar Still CFD Simulation training informative and effective. If you have any further questions or need more insight into specific processes or applications, please don’t hesitate to reach out. Your enthusiasm for the subject is truly appreciated!
Jarvis Homenick MD –
I found the summary of the setup very detailed! It appears to cover all aspects of the analysis. Could you provide some examples of practical applications for this type of solar still technology?
MR CFD Support –
Certainly! This type of solar still technology is often used in regions with limited access to fresh water resources. It’s particularly suitable for small-scale desalination applications, such as providing drinking water in remote areas, for individual households or small communities. Additionally, it can be used in emergency situations or in arid regions to generate fresh, potable water from saline or brackish sources using renewable solar energy.
Marlen Swift –
This product made understanding the species transport model so much clearer! Visualizing vapor behavior in solar stills is fascinating, and it was helpful seeing how each component of the system contributed to the process of desalination.
MR CFD Support –
We’re thrilled to hear the training module on solar still desalination helped clarify the species transport model for you! Thank you for sharing your enthusiasm about visualizing vapor behavior within the system. Our goal is to provide clear and insightful learning experiences, and reviews like yours confirm we’re on the right path. If you have more feedback or need further learning materials, please don’t hesitate to reach out.
Tad Dickens –
The material was extremely informative, especially the detailed explanation of the species transport method. I’ve gained a clear understanding of how vapor production is analyzed without the heavy computations of simulating saline water flow. Great tutorial!
MR CFD Support –
We greatly appreciate your positive feedback on our Solar Still CFD Simulation Training! We’re delighted to hear that you found the material to be beneficial and that the tutorial helped in understanding the species transport method effectively. Thank you for taking the time to review our training product.
Zola Buckridge –
I’m really impressed with the level of detail in the Solar Still CFD Simulation Training. The incorporation of a UDF for surface evaporation seems key to accurately representing the desalination process. Is the user-defined function provided as part of the training or do we need to write it ourselves?
MR CFD Support –
Thank you for your compliment on the Solar Still CFD Simulation training. The UDF for surface evaporation is a critical component to simulate the desalination process accurately. The training material includes the UDF, and it guides you through how to implement it effectively in ANSYS Fluent to complete the simulation process.
Shea Ebert PhD –
The training was very informative, and the step-by-step instructions made it easy to follow along. I especially appreciated the clear explanations about setting up the Species Transport Model. It helped me understand the vapor production process in the solar still device.
MR CFD Support –
Thank you for your kind words! We’re thrilled to hear that you found our training informative and easy to follow. Understanding the vapor production process is crucial for effective CFD simulation of solar desalination units. We’re glad we could assist in enhancing your knowledge. If you need further assistance or have more questions, don’t hesitate to reach out!
Melvin Gusikowski DDS –
What are the advantages of using the Species Transport model in this solar still simulation compared to a multiphase simulation approach?
MR CFD Support –
Thank you for reaching out with your question. One of the advantages of using the Species Transport model over a multiphase simulation in this solar still setup is computational efficiency. This method simplifies the problem by focusing on the vapor production without tracking the liquid phase, which reduces computational resources and time. Moreover, since the interest is in the amount of vapor, Species Transport provides the necessary data regarding species concentration and distribution inside the chamber.
Meredith Lindgren –
The explanation for the CFD simulation of the solar still is quite impressive! It’s great to see a detailed approach towards understanding desalination.
MR CFD Support –
Thank you for the positive feedback! We’re pleased to know the detailed description of the solar still CFD simulation aided your understanding of thermal desalination processes.
Ima Bashirian –
Can the simulation model other types of solar stills?
MR CFD Support –
While this product is specifically designed for a 3D solar still, we can certainly customize the simulation to model other types of solar stills. Please contact us with your specific needs.
Kitty Runte V –
I’m really thrilled with how detailed the report is for the solar still simulation process! Could you explain how the cold glass surface affects the vapor flow inside the chamber?
MR CFD Support –
Thank you for your appreciation! The cold glass surface serves as a condensation site for the vapor inside the chamber. As the hot vapor rises and comes into contact with the cooler glass, it loses energy and condenses into pure water droplets. This phenomenon is the key to the distillation process in the solar still, as it helps separate the pure water from the original saline solution.
Mrs. Hilma Predovic –
The content is highly informative, thanks! Can you tell me what UDF stands for in this context?
MR CFD Support –
UDF stands for User-Defined Function, which provides a way to implement custom models or boundary conditions that are not available as a standard feature in ANSYS Fluent.
Dr. Henri Schimmel DDS –
The Solar Still 3-D simulation training seems very thought-provoking! Could you shed some light on how the structure of the mesh influences the accuracy and stability of the simulation?
MR CFD Support –
In CFD simulations, the mesh structure significantly impacts the accuracy and stability of the results. A structured mesh typically contributes to the stability and speed of convergence due to the orderly arrangement of elements. For complex geometries, adequate mesh refinement is crucial, especially in regions where high gradients are expected, such as the surface where evaporation occurs. The given mesh size meets these conditions, striking a balance between accuracy and computational resource requirements.
Owen Crooks I –
My compliments on the refined techniques used in the solar still simulation, especially how the Species Transport model streamlined the analysis. The solar still’s design and implementation strategy are fascinating, demonstrating superb user-engineering discourse.
MR CFD Support –
Thank you for your positive feedback! We are thrilled to hear that you found our solar still simulation with the Species Transport model insightful and effective for the desalination unit analysis.
Prof. Zoie Dietrich DDS –
The training session for the Solar Still using the Species Transport Model was illuminating! The inclusion of a UDF for surface evaporation seemed pivotal for the simulation realism. Was this UDF provided in the tutorial material, or did it require user creation?
MR CFD Support –
We’re glad to hear you enjoyed the training session! The User-Defined Function (UDF) for surface evaporation is, indeed, a crucial component of the simulation. Rest assured, it is typically included within the tutorial material. We aim to provide comprehensive guides so that users can replicate the results and understand each step of the process.
Rodrigo Bechtelar Sr. –
The training content for this Solar Still simulation is pretty detailed and comprehensive. I’m interested in knowing if this training includes any guidance on post-processing steps or techniques to analyze the distilled water production efficiency.
MR CFD Support –
Yes, our ANSYS Fluent Solar Still simulation training includes a section on post-processing. In this section, you will learn various techniques to analyze and visualize the results. This includes how to interpret species distribution, temperature fields, and the quantitative evaluation of distilled water production efficiency. We will guide you through using the ANSYS Fluent post-processing tools to extract meaningful insights from your simulation data.
Miss Reva Medhurst –
I am very satisfied with how clearly the course explains the function and setup of the laminar viscous model and species transport for simulating the solar still. The results perfectly demonstrated the processes of evaporation and distillation occurred effectively.
MR CFD Support –
Thank you so much for your positive feedback! We’re glad to hear that our course on Solar Still (3-D) CFD Simulation Training was able to provide a clear understanding of the processes and mechanisms of desalination through simulation. It is wonderful to know that the results fulfilled your expectations and effectively demonstrated the key concepts.
Amari Roberts –
What a detailed and practical guide on solar still desalination simulation! After studying the provided material, I am quite impressed with the hands-on approach to understanding species transport in such systems. However, I realized I have one clarification to seek regarding the practical implementation: once we simulate and confirm the operational effectiveness of the model, could you suggest any real-life parameters or conditions we might need to consider when scaling up from this simulation to a fully operational plant?
MR CFD Support –
Thank you for your appreciation and for reaching out with such a thoughtful question! When scaling up from simulation to a full-scale operational desalination plant, real-life parameters that should be considered include material durability against consistent exposure to salinity and temperature fluctuations, energy efficiency with respect to solar energy utilization, the ability to maintain a constant temperature gradient for the efficient condensation of vapor, and the real-life efficacy of heat flux in different climate conditions. Additionally, scalability in terms of modular expansion, maintenance procedures, operational costs, and the impact on the local environment and marine life must also be evaluated. It is essential to undertake a comprehensive feasibility study to assess these parameters vividly to ensure the transition from simulation to reality is as efficient as possible.
Dr. Kelton Hammes –
I am very impressed by the way the Species Transport model was used in this simulation to streamline the desalination process assessment. The setup optimizes computational resources by focusing on the vapor quantity rather than the multiphase flow of the saline water.
MR CFD Support –
Thank you for your positive feedback! We’re glad to hear that you appreciate the efficiency and effectiveness of using the Species Transport model in our Solar Still CFD simulation training. Our goal is to help users understand complex physical processes while also providing a learning experience that is both comprehensive and resource-conscious.
Jorge Kris –
The training was incredibly detailed and the step-by-step approach made it easy to follow. The use of the Species Transport Model simplified the simulation and the assumptions made were clearly stated, aiding my understanding of the desalination process through the solar still. Moreover, the explanation of the governing equation for the gaseous species flow was particularly helpful. The session on initializing the simulation provided a solid foundation for setting up my own models in the future. Kudos to the MR CFD team for effective teaching techniques and robust simulation methodology.
MR CFD Support –
Thank you very much for your positive feedback! We’re delighted to hear that you found the training detailed and easy to follow. Our team at MR CFD prides itself on providing clear and comprehensive learning materials, and it’s great to know that our approach to teaching the Species Transport Model has been helpful to you. We are also pleased that the explanation of the governing equations contributed to a greater understanding of the simulation process. We appreciate your kind words and are here to support you in your future simulation ventures. If you have any more questions or need further assistance, feel free to reach out!
Giuseppe Baumbach –
What a detailed and impressive approach to solar desalination simulation! The careful consideration of physical parameters and the use of species transport is commendable. Great job MR CFD in explaining such complex processes in an understandable way.
MR CFD Support –
Thank you very much for your kind words and appreciation of our Solar Still simulation experience. We strive to provide a clear and comprehensive explanation of the complexity behind CFD simulations, and we’re thrilled to know that our efforts are helpful to our users. If you ever have more questions or need further clarifications about our products, don’t hesitate to reach out.
Lennie Brakus I –
I just completed the Solar Still CFD Simulation Training with ANSYS Fluent, and I’m really impressed with the quality of the content provided. The step-by-step guidance helped me thoroughly understand the species transport model and its application in simulating thermal desalination. I could not have grasped the detailed setup of the boundary conditions or the species transport equations without the clear instructions and well-structured course material. This training equipped me with valuable skills for my research in desalination technology.
MR CFD Support –
We are thrilled to know that you enjoyed the Solar Still CFD Simulation Training and found it beneficial for your research! Hearing that our training materials provided clarity and enhanced your understanding of species transport modelling really validates the hard work our team puts into creating comprehensive and high-quality educational content. Thank you for your kind words, and we wish you the best in your desalination technology research. If you have any further inquiries or need more assistance, please feel free to reach out!
Shaun Monahan II –
The CFD tutorial for the solar still is amazing! The step-by-step guidance ensured I fully understood how to set up and simulate the desalination process. The attention to detail, especially in defining boundary conditions and utilizing the Species Transport method, has given me a solid grasp of the entire workflow within ANSYS Fluent. Excellent job compiling the training material – it flowed logically and made a complex process truly understandable.
MR CFD Support –
Thank you for your remarkable feedback! We are elated to hear that the tutorial on the solar still desalination process using ANSYS Fluent has significantly contributed to your understanding of the simulation workflow. It is truly gratifying to know the detailed instructions on Species Transport and boundary conditions setup were helpful to you. Should you need any further assistance or have more questions on any aspect of CFD applications, feel free to reach out!
Bridgette Stoltenberg –
I’m very impressed by the attention to detail in the CFD simulation process for the solar still! The step by step explanation of the methodology was clear and insightful. The inclusion of the UDF for surface evaporation demonstrates commitment to creating realistic predictions. Amazing work!
MR CFD Support –
We’re thrilled that you appreciate the complexity and detail of our solar still CFD simulation. Your feedback is of great value to us. Thank you for taking the time to share your positive experience with our product!
Ms. Mckayla Ondricka DVM –
The simulation tutorial was a clear guide to setting up the steady-state species transport model for desalination! I particularly appreciated the detailed step-by-step process and assumptions provided. Fantastic work!
MR CFD Support –
Thank you for your kind words and positive feedback on our Solar Still desalination CFD simulation tutorial. We’re delighted to hear that you found the guide clear and informative. If you have any more questions or need further assistance with your simulations, please feel free to reach out.
Dennis Brakus –
What a remarkable example of applying theoretical concepts to practical problem-solving! The detailed undertaking of simulating a solar still using ANSYS Fluent’s Species Transport Model underscores not only MR CFD Company’s ability to harness complex computational techniques but also their commitment to resource sustainability through desalination studies. The structured mesh approach and the employment of a User Defined Function to simulate evaporation exhibits the product’s versatility and user-centric development. Furthermore, by focusing on the production of vapor and ensuring the conservation of energy within the system, the product exemplifies its educational and practical value for those interested in alternative energy solutions. Congratulations to the MR CFD team on developing a thorough, instructive simulation package!
MR CFD Support –
We are thrilled to receive your positive feedback on our Solar Still CFD Simulation Training! It gives us great pleasure to know that the education and application value of our product met your expectations. Your acknowledgment of the detail and rigor applied in our simulation efforts to deliver an accurate depiction of a solar still enriches our dedication to addressing sustainability and alternative energy topics. Your commendation is sincerely appreciated, and we look forward to providing you with more quality learning materials in the future. Thank you for taking the time to recognize our efforts!
Stefanie Muller –
Just received my Solar Still design by Species Transport Model training from MR CFD, and I must say, the tutorial was incredibly enlightening. The explanations of the Species Transport method helped clarify many of my previous confusions and the focus on vapor production gave me insights into the desalination process that were quite intricate. Thanks to this, I feel more equipped to tackle my own simulations in the future!
MR CFD Support –
Thank you so much for your kind words! We’re absolutely thrilled to hear that our Solar Still by Species Transport Model training provided you with valuable insights and clarification for your simulations. It’s always our goal to empower our customers with understanding and skills that support their projects. If you have more queries or need further assistance in the future, don’t hesitate to reach out. Thanks again for choosing MR CFD!
Dr. Jan Walsh –
This training sounds perfect — exactly what I needed to get familiar with species transport in solar stills. How accurately does this model reflect real-world performance?
MR CFD Support –
Thank you for your kind words! We strive to ensure that our models are detailed and reflect real-world performance to a great extent. We combine theoretical data with computational fluid dynamics tools to deliver simulations that closely mimic actual operations. While all models have limitations and are simplifications of reality, we believe that our solar still simulation, with the species transport method incorporated, provides accurate insights into the performance of a desalination unit under the given assumptions and conditions.
Gina Carter –
I am very impressed with how the Species Transport Model was used in this simulation. Some simulations get too complicated with multiphase modeling, but this seemed just perfect for vapor tracking. This might be unique to the solar still desalination setup, right? The solution methods and the initialization process look carefully selected – great job on keeping the simulation efficient yet accurate!
MR CFD Support –
Thank you so much for your kind words! We’re thrilled to hear that you found the Species Transport Model approach satisfactory and efficient for the solar still desalination simulation scenario. You’re correct that using this model allows for accurate vapor tracking without overly complicating the simulation with a multiphase model. We always strive to provide a balance of precision and computational efficiency. Your appreciation means a lot to us and motivates us to continue delivering high-quality CFD training materials.
Dr. Loren Brown –
I’ve appreciated learning through the simulation of the solar still for desalination using ANSYS Fluent. The step-by-step breakdown provided a clear overview of the process which made the complex species transport model approachable. The addition of the UDF for surface evaporation was particularly insightful, and it was fascinating to see how the simulation effectively calculates vapor production without the need for simulating saline water flow. The thorough detailing in temperature and boundary conditions set within the simulation also played a crucial part in making the experience seamless.
MR CFD Support –
Thank you for the positive review of our Solar Still (3-D) CFD Simulation Training using the Species Transport Model in ANSYS Fluent. We’re delighted to hear that you found the tutorial insightful and user-friendly, particularly regarding the UDF for surface evaporation. Our goal is always to provide clear and efficient learning materials, and it’s great to know we’ve succeeded in your case. We appreciate the time you took to write about your experience, and we look forward to assisting you in the future.
Jena Denesik –
I recently completed the Solar Still (3-D) by Species Transport Model training, and I must say I’m thoroughly impressed. The use of a UDF for surface evaporation was a smart approach. The simulation captured the essence of real-life solar stills and provided an in-depth understanding of the desalination process. Kudos to MR CFD for an exceptional tutorial!
MR CFD Support –
Thank you for your kind words! We’re delighted to hear that our training provided you with comprehensive insight into solar thermal desalination and that you appreciated the application of UDF for surface evaporation in the simulation. Your positive feedback motivates us to continue creating high-quality and informative CFD tutorials. If you need any further assistance or have inquiries about other products, feel free to reach out. Thanks again for choosing MR CFD!
Dr. Hassie Hoeger I –
This training module seems comprehensive! I really appreciate the use of the Species Transport Model, making the simulation considerably resource-efficient by focusing only on vapor generation.
MR CFD Support –
Thank you for your positive feedback! We’re glad to know the training module met your expectations and you found the implementation of the Species Transport Model effective for simulating the solar still desalination process.