
Operating Pressure
This blog describes the type of pressure like stagnation or total, atmospheric, gauge, and operating pressures. Then we bring the equations of these pressures. Finally, we have thoroughly explained these pressures in ANSYS Fluent software.
Stagnation pressure
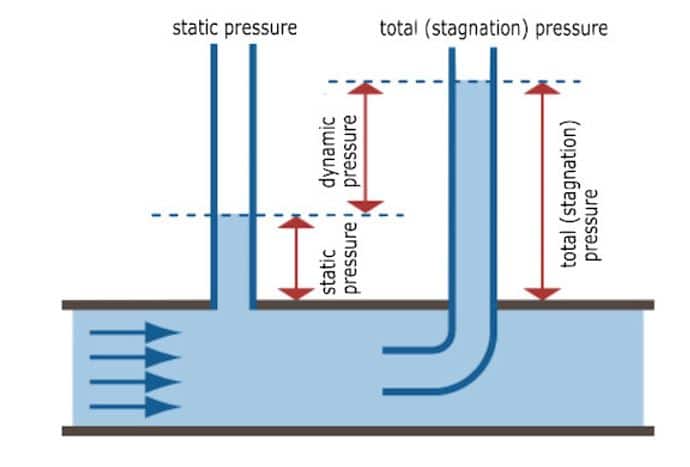
We know that the total pressure equals the sum of the static and dynamic pressure. The static pressure is the fluid pressure in rest, and dynamic pressure is the fluid pressure in moving mode. This fluid can be liquid or gas.
As seen from the equation above, dynamic pressure is dependent on the velocity and density of the fluid, meaning that with increasing the velocity and density of the fluid, dynamic pressure is increasing.
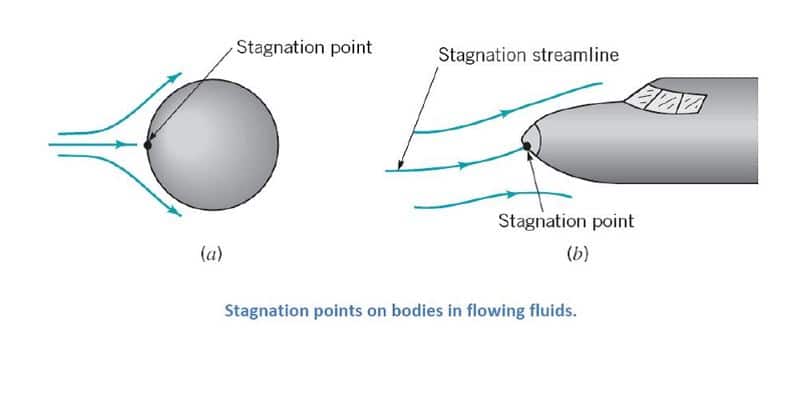
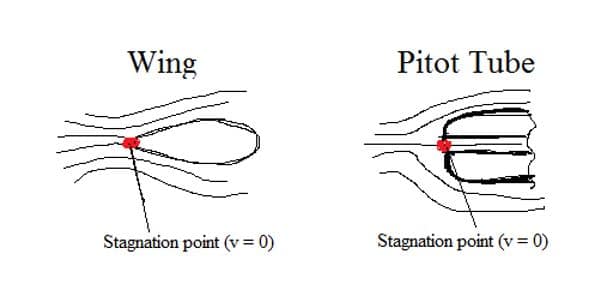
According to the figure above, the velocity of the fluid at the specified point is zero, and since the velocity is zero, the dynamic pressure is also zero:
So at the specified point, we have the maximum static pressure. This point is also called the stagnation point; we have the maximum static pressure in this case. The fluid velocity V becomes zero at the stagnation point, and the kinetic energy is converted into a pressure rise.
Atmospheric pressure
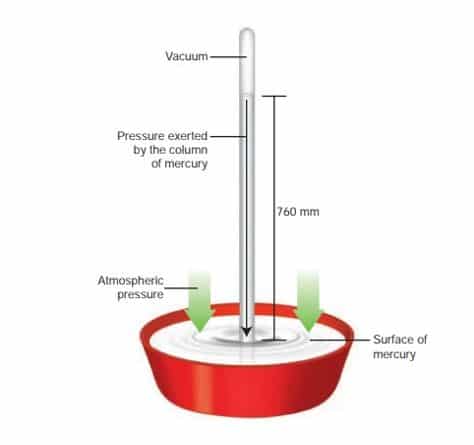
The pressure within Earth’s atmosphere is referred to as atmospheric pressure, or barometric pressure. A barometer is a device that measures the pressure in the atmosphere. We can use the Mercury barometer in a lab or weather station, etc.
The height of the mercury column on an average day at sea level is 760 mm. Let’s figure out the pressure due to the 760 mm mercury column, which equals atmospheric pressure. The density of Mercury is 13600 kg/m3.
One atmospheric pressure is the name given to this pressure (atm). A unit known as (bar) is also used to express such high-pressure values.
1 atm=101325 pa or 1 atm=1.01325 bar
The value is 101.325 kPa when expressed in kilopascals. This means that the force acting on each 1 m2 of the surface is 1.01325 KN.
Gauge pressure
The force applied to an area is known as pressure. Pressure can be measured in various ways, with gauge and absolute pressure being two of the most typical. The difference between measured and local air pressure is known as a gauge or relative pressure. If the measured pressure is less than the atmospheric pressure, the gauge pressure might have a negative value.
You can see the gauge pressure formula as below:
Operating pressure
You can ignore air pressure frequently by pressure gauges, resulting in a reading of zero at atmospheric pressure. As a result, Gauge pressure defines as the pressure corresponding to atmospheric pressure. For pressures over atmospheric pressure, gauge pressure is positive, while for pressures below atmospheric pressure, it is negative.
The absolute value of the force per unit area exerted on a surface by a fluid is referred to as absolute pressure. The difference between absolute and atmospheric pressure shows using gauge pressure.
Operating Pressure, Gauge Pressure, and Absolute Pressure in ANSYS Fluent software
To determine the pressure in incompressible flows, we can use Bernoulli’s formulation, and for compressible flows, also we can use the isentropic formulations.
-
Pressure in incompressible flow
In incompressible flows, the total pressure and static pressure in the Bernoulli equation are related to the velocity inlet.
-
Pressure in compressible flow
In compressible flows, we use isentropic relations for the ideal gas to establish a relationship between total pressure, stagnation pressure, and velocity at the pressure inlet boundary. Therefore, the value of total pressure entered by the user at the inlet boundary and the static pressure in the adjacent fluid element are related as follows.
Where:
The operating pressure appears in the equation because the amount of inlet boundary conditions are in terms of pressure relative to operating pressure. As explained in Setting up: solver, in compressible flows, the density is one of our unknowns, which is calculated from the following equation.
For gas mixtures of several species, the specific gas constant, R, determines using a molar or mass fraction. We can determine the amount of static temperature at the inlet by the total temperature entered by the user.
In ANSYS Fluent, all of the pressure that users determine and calculated pressures are gauge pressure.
How to go to the operating pressure task page?
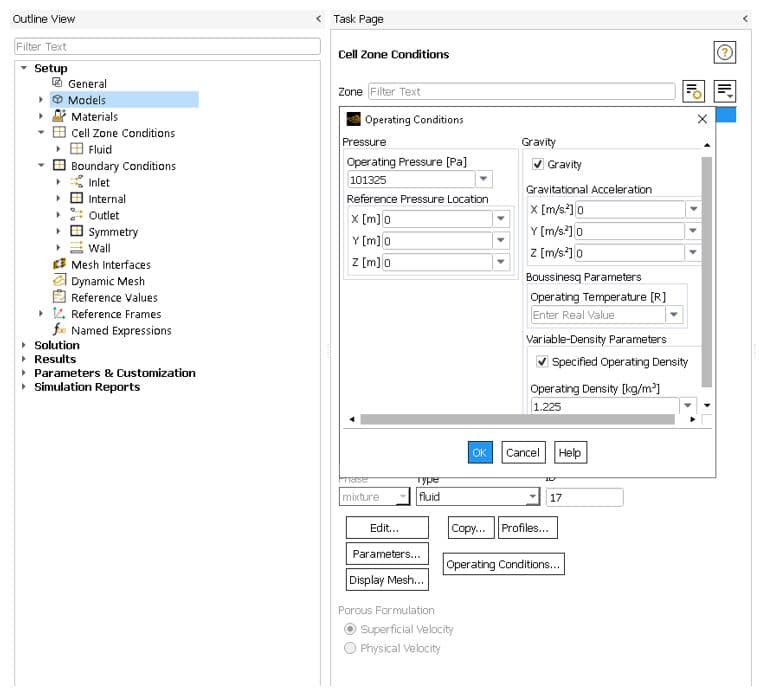
To set the operating pressure in ANSYS Fluent, apply the following path:
Physics >> operating pressure or setup >> cell zone conditions >> operating conditions…
According to the above figure, the default operating pressure in ANSYS Fluent is 101325 pa.
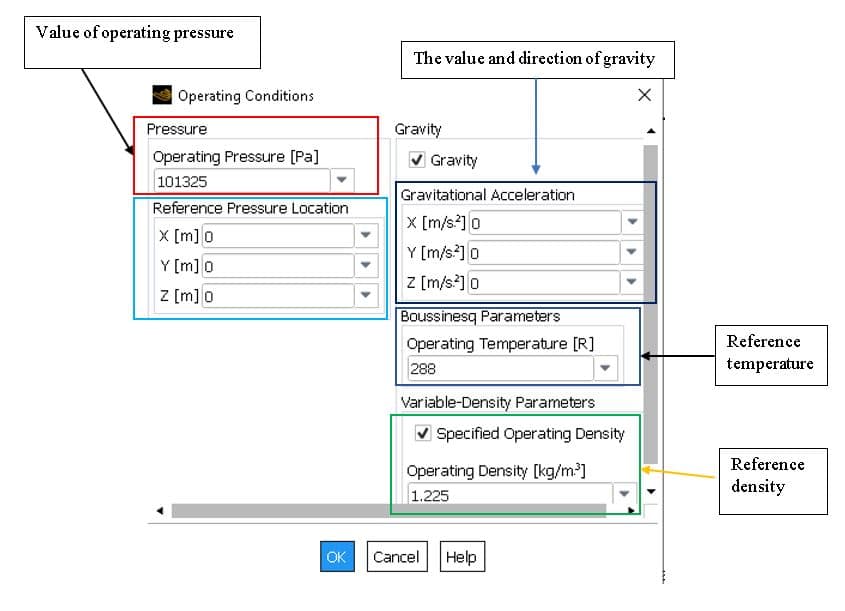
We show the sections of operating pressure as below:
The total pressure is the same as the relative pressure (Gauge) relative to the reference pressure defined in the Operating condition panel in the figure above.
Reference pressure location with type of pressure boundary conditions and without it
When there were pressure boundary conditions like pressure inlet, etc., we didn’t need to set the Reference pressure location, but when there weren’t pressure boundary conditions, it needed that determine the reference pressure location in a point of Computational point.
Summary
Consider a flow inside a pipe in which a fluid flow moves at a certain speed. According to the no-slip condition established on the walls, we know that the velocity of the fluid flow on the wall is zero.
Using a pitot tube to measure this pressure gives us this amount of static pressure. But if we put the pitot tube in the center of the tube, we will have the total pressure shown in the figure below:
We can summarize this section as follows:
- The stationary fluid has Static Pressure.
- The fluid which has moved has Dynamic Pressure.
- Total pressure = Static pressure + Dynamic pressure.
- The total pressure in any fluid remains constant, and static and dynamic pressure changes. (example: If a fluid is flowing in a nozzle, the dynamic pressure increases and static pressure decreases).
- In incompressible flows, the total pressure and static pressure in the Bernoulli equation are related to the velocity inlet, and in compressible flows, we used isentropic relations.
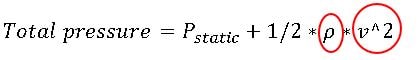
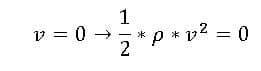
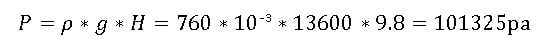
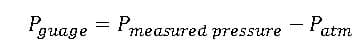
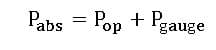
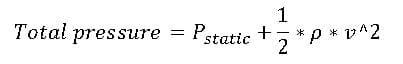
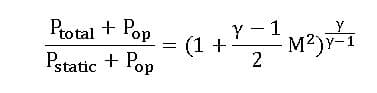
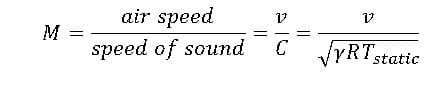
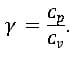
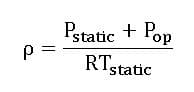
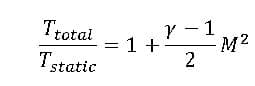
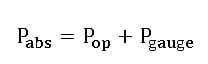



This Post Has 0 Comments