
Reference Values
Reference Values
In this article, you will find formulas for several important Dimensionless numbers (Lift, Drag, Pressure, pitching moment, and Convective Heat Transfer coefficient ), Friction drag, Reynolds number, Nusselt number, and then the applications of reference value in ANSYS Fluent. Typically, these equations are written Non-Dimensionally using dimensionless values obtained using appropriate characteristic scales.
There are many benefits to using Dimensionless variables. This reduces the number of variables appropriate for a problem and helps to determine the size of the terms of the conservation equations that are related and thus the sentences that can be ignored.
Dimensionless Form of Equations
Differential equations that represent conservation laws are rarely used with dimensional equations.
Kinetic Energy
Given that we deal with kinetic energy in many numbers, most Dimensionless numbers, we describe it.
We know that the kinetic energy equation equals 1/2*m*v2; now, how can I obtain the mass of water or air?
The answer to this question is the density or specific mass. Density is the mass of unit volume fluid.
Therefore, the kinetic energy of the fluid is equal to 1/2*ρ*v2. The specific mass of air is the mass of air per unit volume, but to get this value, for example, under the wing of an airplane, I have to calculate the total area under the wing, so we have to multiply the kinetic energy by the area of the wing 1/2*ρ*v2*s.
Where:
- ρ is the density of the fluid [kg/m3]
- v is the velocity of freestream flow [m/s]
- s is the area [m2]
This parameter will use in the following formulas.
Lift Coefficient
By flying fast through the air, the aircraft produces Lift. The vehicle’s wings have cross-sections that resemble airfoils. A pressure difference between the top and lower wing surfaces will be produced for a given flow speed with the airfoil positioned at an angle of attack to the approaching airstream. A high-pressure area will be below, and a very low-pressure area will be above. Lift is produced on the wing by the difference in these pressure forces. The amount of lift generated will depend on the size of the airfoil, its square velocity, the air density around it, and the angle at which the wing is attacking the incoming flow.
We can define the lift coefficient as:
Drag Coefficient
The drag coefficient or , which has non-dimensions is employed in fluid dynamics is a measurement of an object’s drag or resistance in a fluid environment like air or water. A lower drag coefficient means the object will have less aerodynamic or hydrodynamic drag, which it uses in the drag equation.
Pressure Coefficient
In fluid dynamics, the dimensionless number’s pressure coefficient describes the relative pressures present throughout a flow field. Aerodynamics and hydrodynamics both use the pressure coefficient. In a fluid flow field, each point has a specific pressure coefficient.
Pitching Moment Coefficient
The aerodynamic Pitching moment coefficient generates using aerodynamic forces applied to the body that tend to rotate the body. This object can be the wing of an airplane, a car, or a wind turbine blade. The rotation occurs when this rotational force applies outside the center of pressure or the aerodynamic center.
Friction Drag
The friction drag coefficient uses to characterize the friction drag brought on by shear stresses.
Reynolds Number
For defining the flow processes for Forced flows, the Reynolds number is a dimensionless similarity parameter.
When it comes to objects surrounded by flow, the characteristic length x used to get the Reynolds number is equal to the length of the object direction of the flow.
Nusselt Number
The Nusselt number describes the ratio of convective heat transfer compared to heat conduction.
Where x denotes the characteristic length of the system
h is the Convective Heat Transfer Coefficient and Its definition is given below:
Convective Heat Transfer Coefficient
You can define the convective heat transfer coefficient, h, as follows:
The heat transfer rate per unit surface area and unit temperature difference between a solid surface and a fluid.
q is the local heat flux [W/M2]
is the difference in temperature ( is the difference between wall temperature, Twall, and the bulk temperature, T∞)
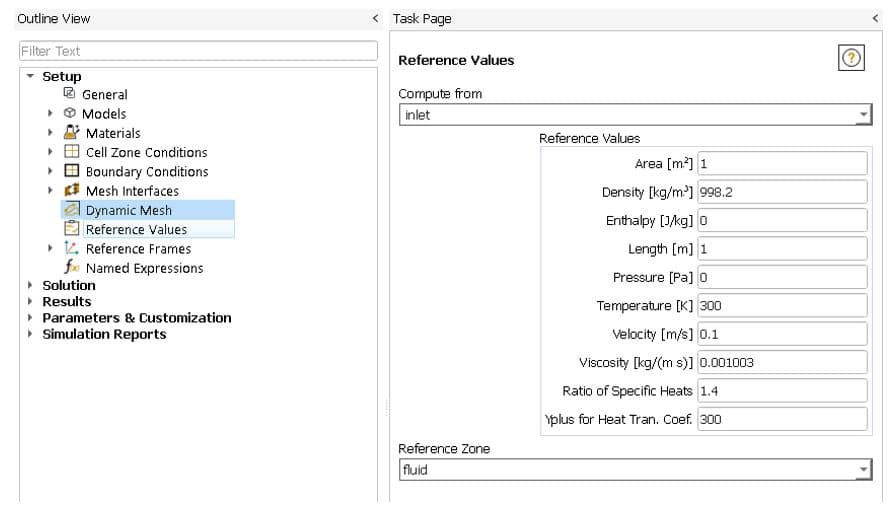
Application of Reference Value
To go to the reference value of the task page, we apply the following path:
Setup>> reference value
It contains inputs for the reference values.
The Reference Values to be Set are:
Area, Density, Enthalpy, Length, Pressure, Temperature, Velocity, dynamic
Viscosity and Ratio Of Specific Heats.
Area
We can use this parameter to find coefficients such as Lift, Drag, and momentum or pich:
Density
Used for the calculation of Force and Moment coefficient and Re:
Velocity
Used for the calculation of Forces and Moment coefficient and Re:
Depth
determines the reference depth for 2D cell volume computation (by default set as 1 m).
Enthalpy
Establishes the reference enthalpy, which controls the overall change in enthalpy.
Length
Used for the calculation of Force and Moment coefficient and Re:
Temperature
Temperature uses for the calculation of heat transfer coefficient and entropy.
Viscosity
This parameter uses for evaluating the Reynolds number
The Ratio of Specific Heat
It uses for the efficiency of turbomachinery.
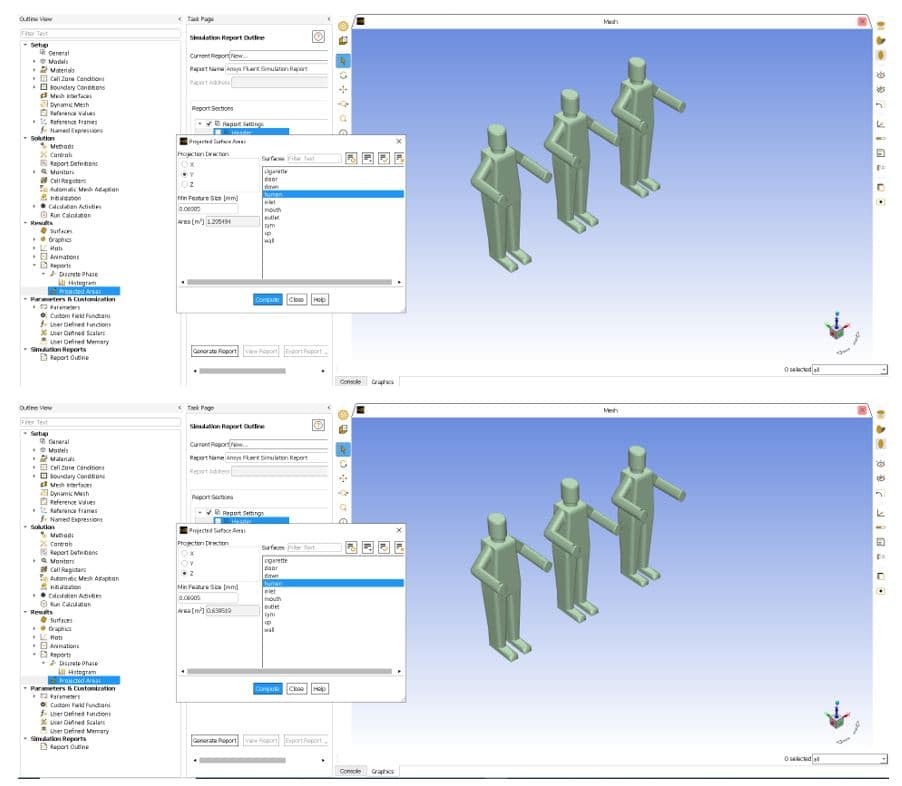
Projected Area
The surface area can refer to either the surface area perpendicular to the flow, or the surface area projected in the flow direction, depending on which form of drag predominates.
To find the projected area in fluent, we can apply the following path:
Results>>Reports>>Projected Areas
As you can see, the projected area in the flow direction (Y-Projected Direction) and the projected area perpendicular to the flow (Z-Projected Direction) are 1.295494 and 0.639519 [m2], respective.
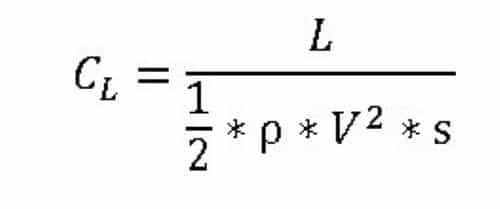
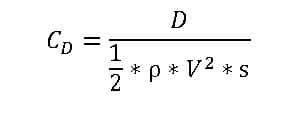
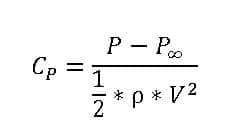
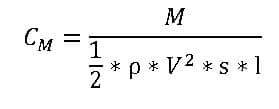
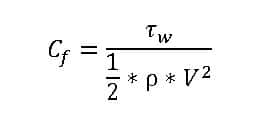
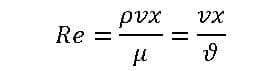

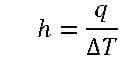
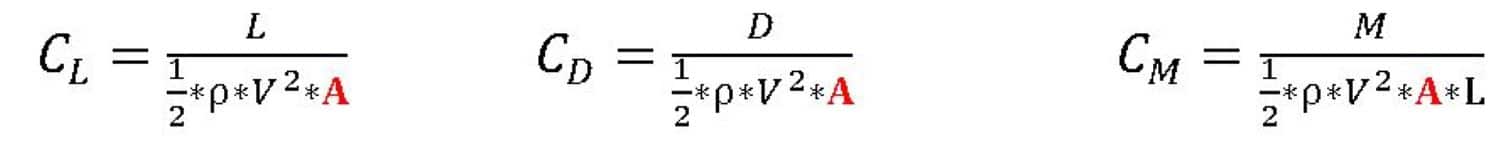
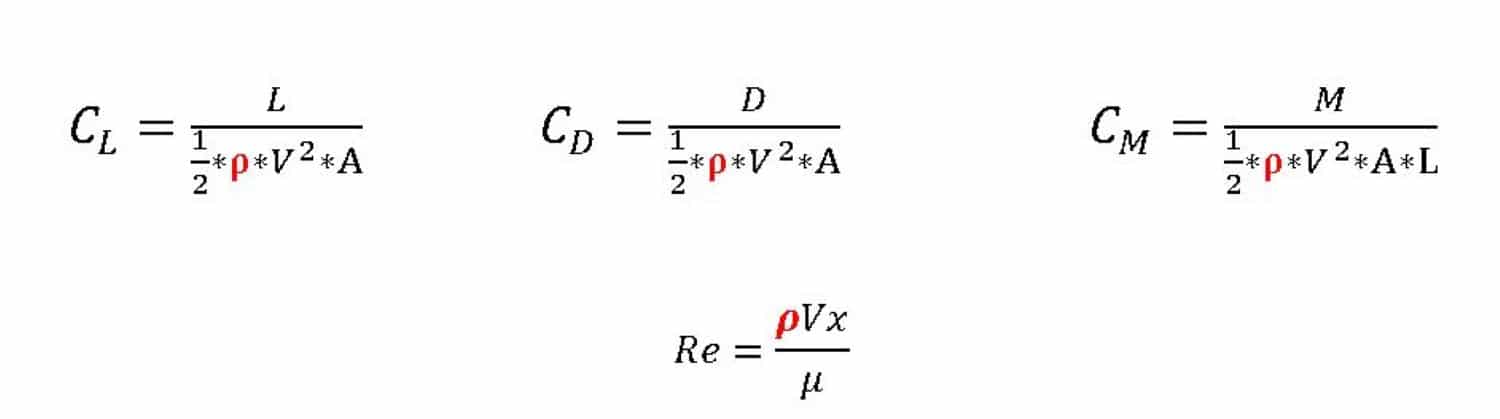
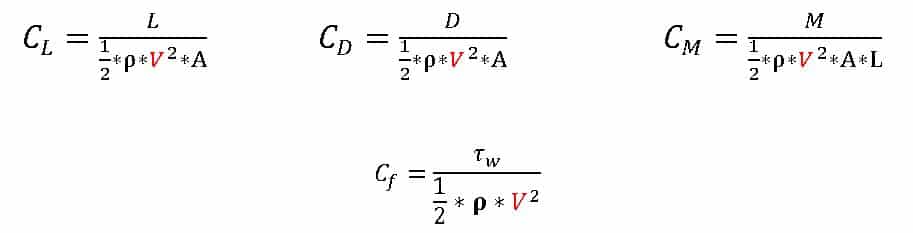
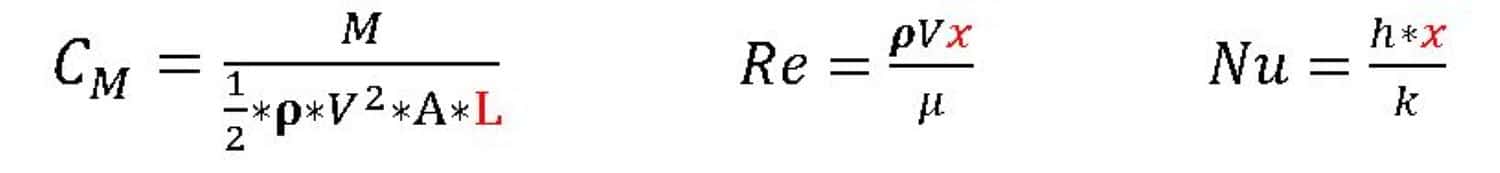
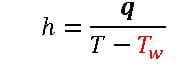
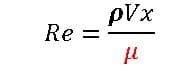
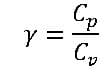




This Post Has 0 Comments