Cavitation in a Radial Flow Pump CFD Simulation
$200.00 Student Discount
- The problem numerically simulates the Cavitation in a Radial Flow Pump using ANSYS Fluent software.
- We design the 3-D model by the Bladegen software.
- We mesh the model with Turbogrid software, and the element number equals 63308.
- We use the Frame Motion (MRF) to define rotation movement.
- We use the VOF Multi-Phase Model to define water liquid and water vapor.
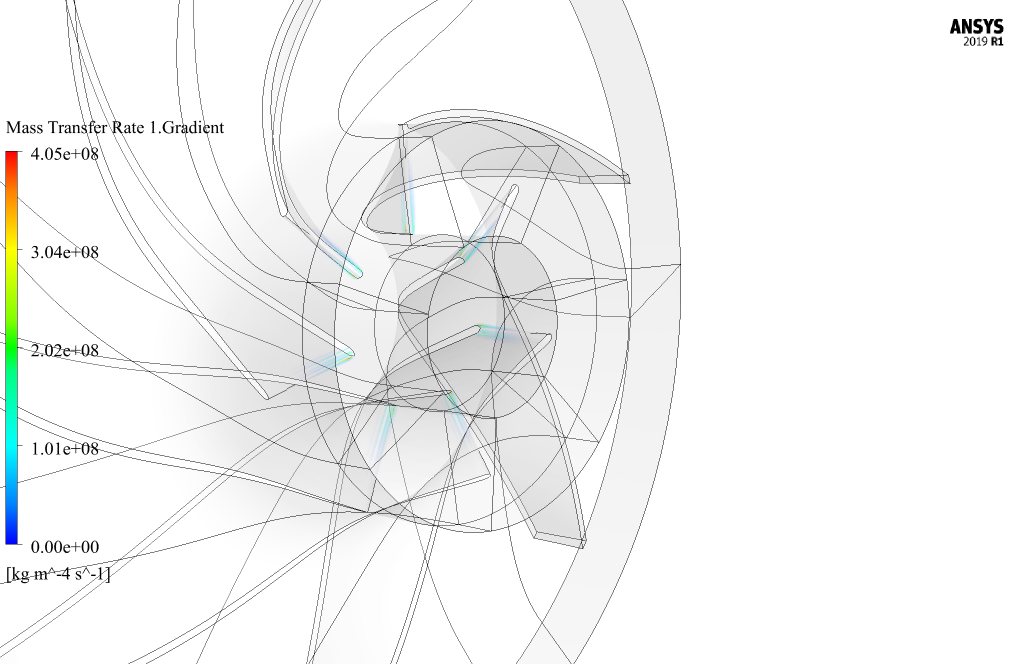
- We define a mass transfer between water and vapor to consider Cavitation.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Cavitation in a Radial Flow Pump CFD Simulation, ANSYS Fluent Tutorial
This product stimulates the cavitation phenomenon inside a radial flow pump using ANSYS Fluent software. We perform this CFD project and investigate it by CFD analysis.
This pump is of the centrifugal pump (radial flow) type; In this way, the desired fluid enters it parallel to the central axis and exits it radially or perpendicular to the inlet path. These pumps are commonly used to create high pressures at low flow rates and are also the most common type among pumps.
The cavitation phenomenon occurs when the pressure of a liquid falls below its vapor pressure at a constant temperature. In this case, the fluid turn from liquid to vapor, forming a bubble. This process is called cavitation.
Now, if these bubbles are transferred to the high-pressure parts of the pump, they will collapse. This collapse of the bubble creates a vacuum locally, as a result of which the liquid around the bubble moves towards the empty space at a very high speed and pressure.
Radial Flow Pump Methodology
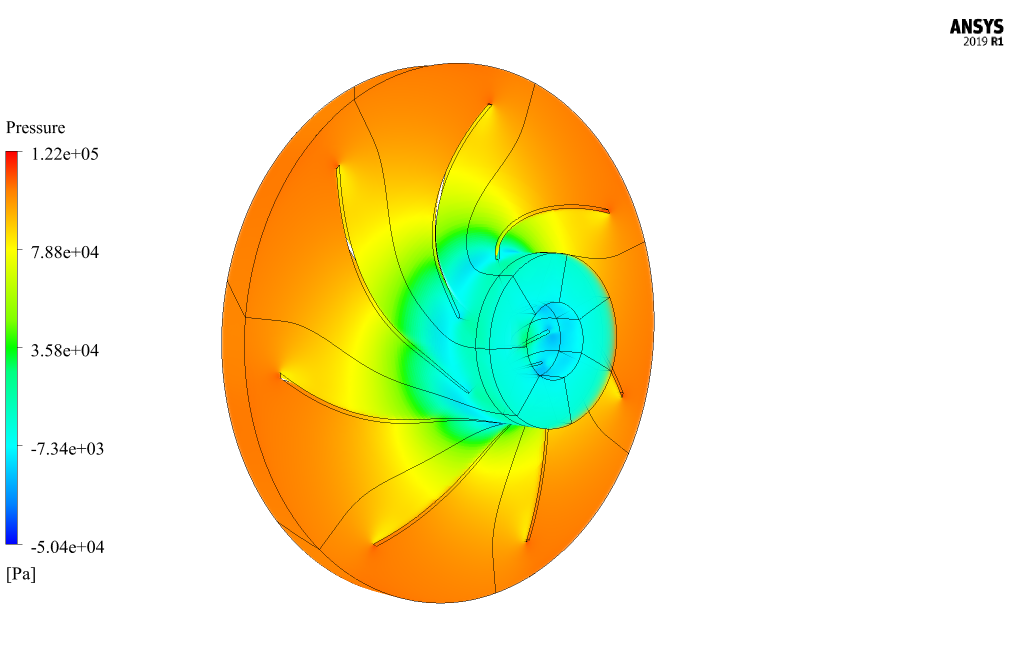
The working fluid used in this pump is liquid diesel; Thus, it has a density equal to 830 kg.m-3 and a viscosity equal to 0.00332 kg/m.s. Since pumps are devices that work inherently based on pressure changes, in this modeling, the pressure boundary condition at the inlet and outlet boundaries of the pump is used.
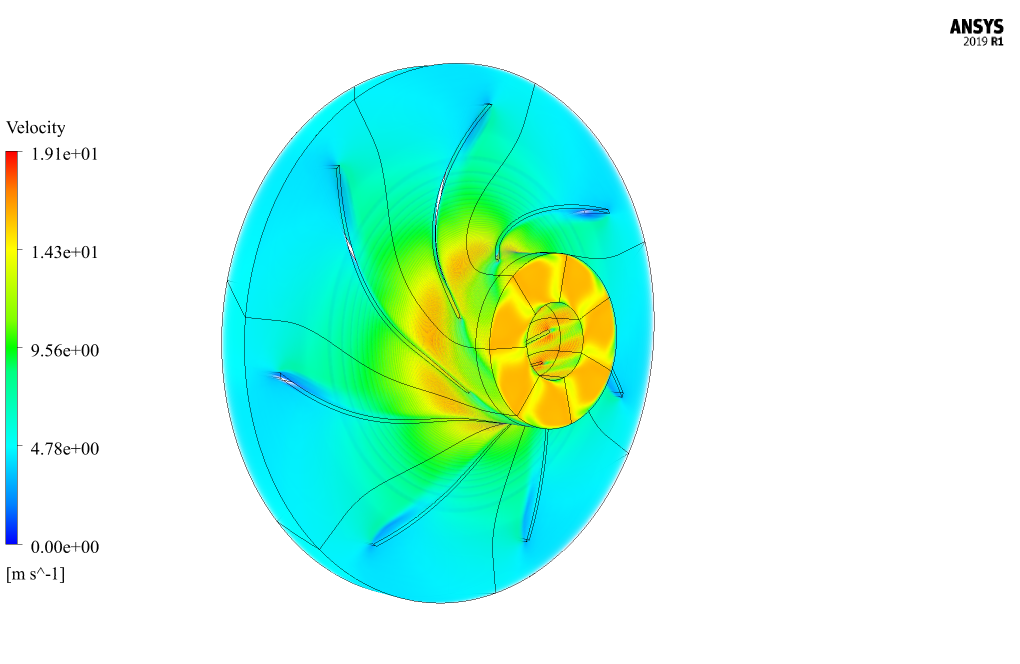
Thus, the liquid diesel flow enters the pump axially with a pressure of 0 pascal and exits it radially with a pressure of 109872 pascals. Also, to define the rotation of the fluid inside the pump, a frame motion (MRF) tool with a rotational speed equal to 20 rad/s has been used.
This process in areas close to the inner walls of the pumps and especially in the areas adjacent to the blades causes the liquid to hit the walls and blades with high force and, as a result, leads to damage to the pump and eventually shortens its life.
Therefore, one of the industry’s most critical issues is investigating the possibility of cavitation inside the pumps and solutions to reduce it. So in the present model, another fluid is defined as diesel vapor with a density equal to 9.4 kg/m3 and a viscosity equal to 0.000007, and also the multi-phase VOF model is used.
Thus, the primary fluid of diesel is liquid, and the secondary fluid is vapor diesel, and between these two fluids, a mass transfer is defined in the form of cavitation. The vapor pressure required for cavitation is defined as 50900 pascals.
The present model is designed in three dimensions using Bladegen software. Since the current model is radially symmetrical, only one piece of it can be drawn radially and then expanded around the central axis.
Therefore, the model consists of a single piece that, on the one hand, has an axial flow input section and, on the other hand, a radial output section. On both sides of this piece, the periodic boundary type is used, and a blade is drawn as a curve in the middle.
A radial flow pump with seven blades will be created if we expand this piece around the central axis. The meshing of the present model has been done using Turbogrid software. The mesh type is structured, and the element number equals 63308.
Radial Flow Pump Conclusion
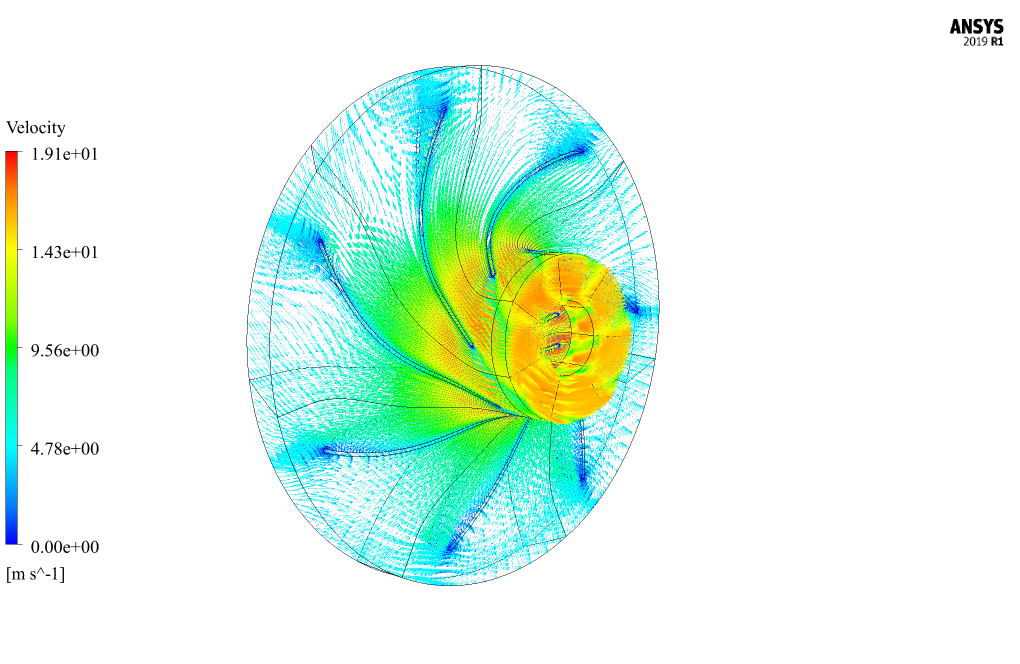
The purpose of this work is to investigate the cavitation phenomenon inside the pump. At the end of the solution process, we obtain three-dimensional contours related to pressure, velocity, vapor phase volume fraction, liquid phase volume fraction gradient, and mass transfer rate gradient.
We also present 3D velocity vectors. The most vital results of this study are vapor volume fraction and mass transfer rate contours that show where the cavitation happened.






Reviews
There are no reviews yet.