Magnetic Field Effect on Nanofluid, CFD Simulation, ANSYS Fluent Training (2-D)
$210.00 Student Discount
- The problem numerically simulates Magnetic Field Effect on Nanofluidusing ANSYS Fluent software.
- We design the 2-D model by the Design Modeler software.
- We mesh the model with ANSYS Meshing software.
- The mesh type is Structured, and the element number equals 9282.
- We use the magnetic hydro-dynamic model (MHD) to investigate the effect of a Magnetic Field on the nanofluid.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Description
The present problem simulates a magnetic field’s effect on a nanofluid in a two-dimensional channel using ANSYS Fluent software. We perform this CFD project and investigate it by CFD analysis.
The present model is designed in two dimensions using Design Modeler software. The model is a channel drawn in two dimensions due to its symmetrical geometry.
This model has a length and width of 0.49 m and 0.01 m; It has an input boundary on the left and an output boundary on the right, and the lower boundary of this area is defined as the central axis. Also adjacent to the channel’s outer wall, a boundary is defined as the fluid and solid region interface.
The meshing of the present model has been done using ANSYS Meshing software. The mesh type is Structured, and the element number equals 9282.
Magnetic Field Methodology
Whenever particles of metal or alloy with tiny dimensions around the nano-scale are mixed inside the base fluid, nanofluid is produced that can have applications such as enhancing heat transfer due to the metals’ conductivity.
Also, in this simulation, the effect of a magnetic field on the nanofluid behavior and its heat transfer has been investigated. Therefore, the magnetic hydro-dynamic model or MHD has been used. The magnetic induction method has been used in the present work to define the magnetic field.
When this method is used, an external magnetic field is generated to apply a specific magnetic flux in different Cartesian coordinates’ directions.
The nanofluid defined in the model is made of iron oxide called Fe3O4 and contains 2% nanoparticles. This applied nanofluid has a density of 1081.158 kg/m3, a specific heat capacity equal to 3841 j/kg.K, a thermal conductivity equal to 0.640835 W/m.K, and a viscosity equal to 0.001055 kg/m.s Is.
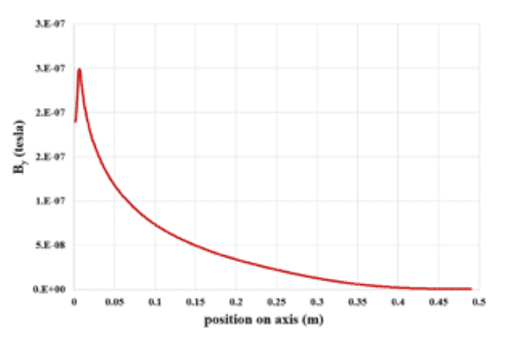
A constant magnetic field is used in the present work, and the magnetic flux equivalent to 1 tesla is defined only along the y-axis or the same as the channel radius.
In terms of boundary conditions, the insulation condition is used for the outer wall of the channel, i.e., no electric current passes, and also for the inner wall and the common boundary between the solid and fluid parts of the model, the Coupling condition is used to transmit electric current bilaterally.
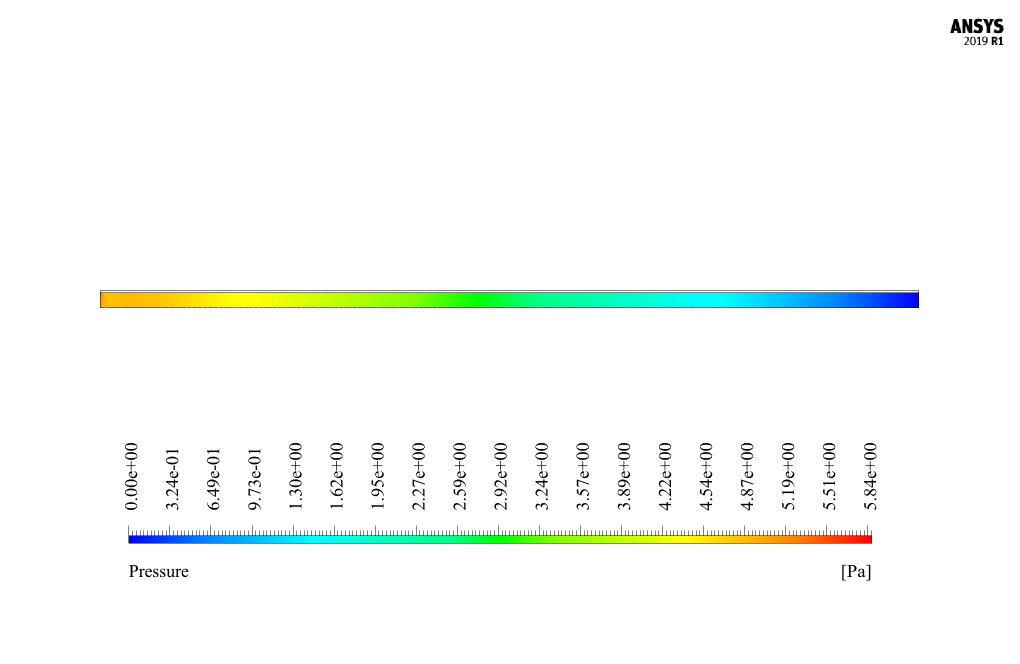
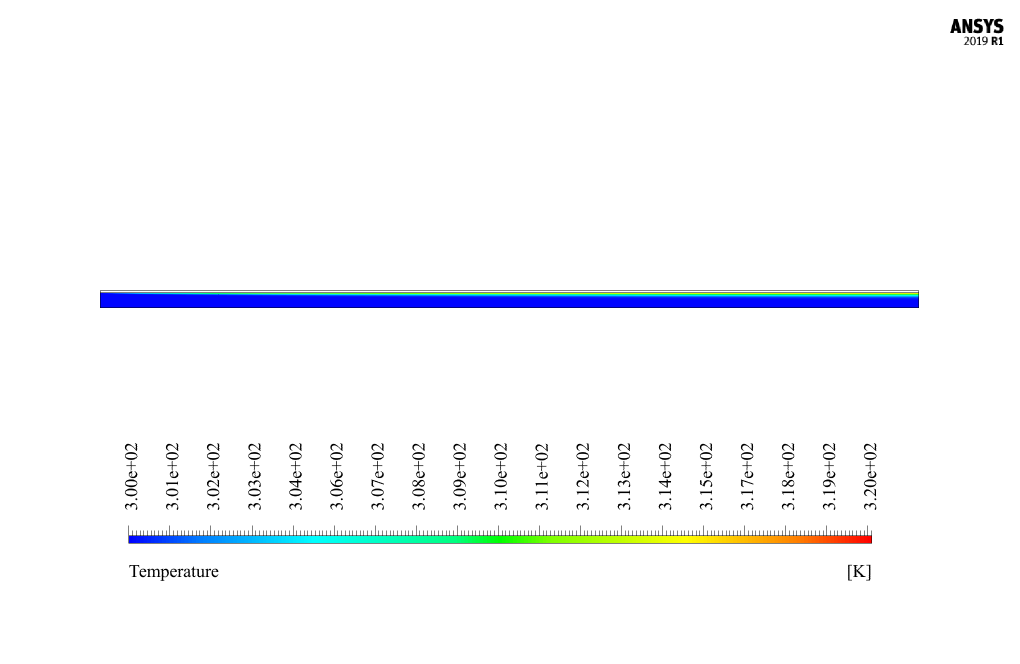
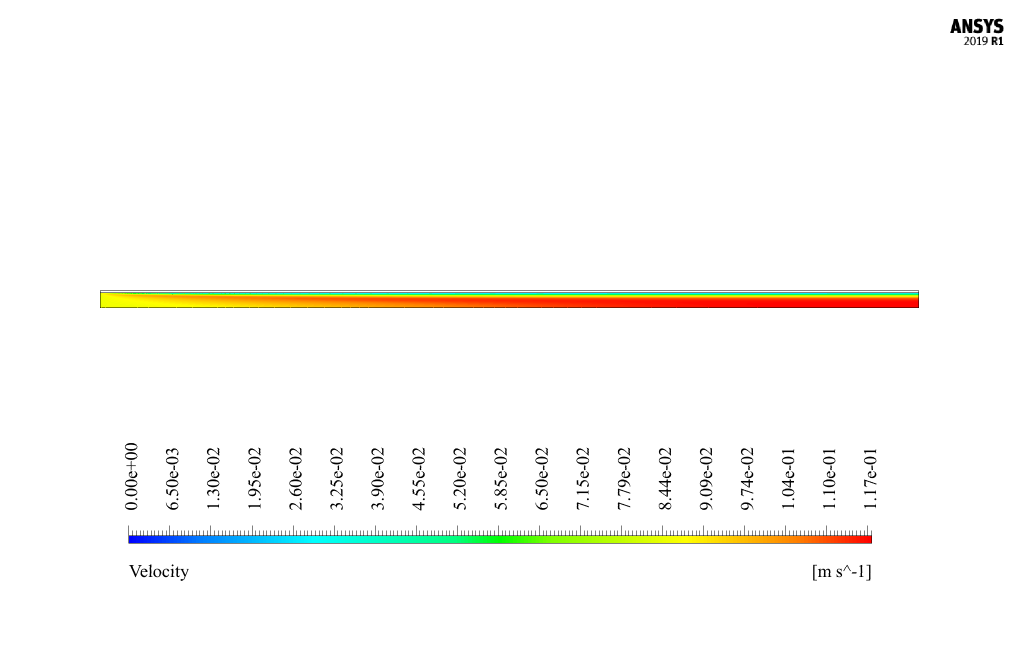
The nanofluid stream enters the channel with a velocity of 0.0837 ms-1 and a temperature of 300 K. It exits the canal with a pressure equal to atmospheric pressure. The channel’s outer wall also has a constant thermal temperature condition of a temperature equal to 320 K.
The laminar model and the energy equation are enabled to solve the turbulent fluid equation and calculate temperature distribution inside the domain, respectively.
Magnetic Field Conclusion
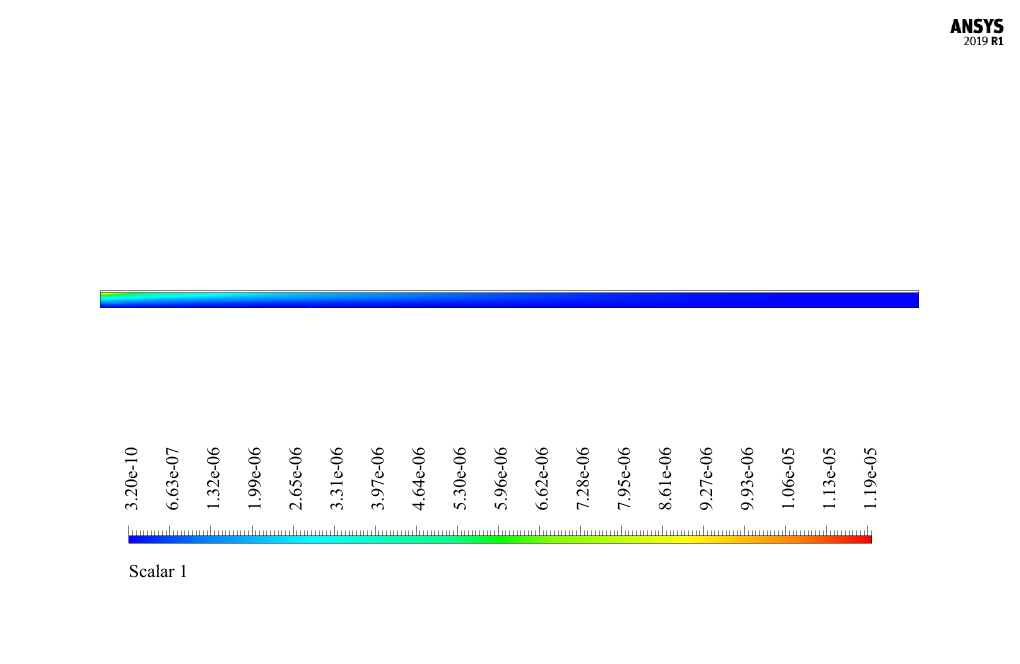
At the end of the solution process, we obtain two-dimensional contours related to pressure, velocity, temperature, and magnetic field in horizontal and vertical directions in the model.
Also, we obtain the diagram of the perpendicular magnetic field changes in the longitudinal direction of the central axis of the channel. The present results show the effect of applying a magnetic field and thermal boundary condition on nanofluid flow and its heat transfer.



Pauline Schiller –
Absolutely insightful tutorial! The integration of magnetic field effects on the behavior of the nanofluid really shed light on how this interaction can enhance heat transfer.
MR CFD Support –
Thank you for your positive feedback! We’re pleased to hear that you found the tutorial on the effects of a magnetic field on nanofluids helpful and insight-provoking. Should you have any more questions about heat transfer or CFD simulations, please don’t hesitate to reach out. We’re always here to help expand your CFD knowledge!
Sylvester Balistreri –
The appliance of magnetic field is amazing in enhancing heat transfer. The magnetic induction technique sounds intriguing. Are special materials or configurations required in practical applications to sustain the magnetic field? And also, how does this apply to industries that rely heavily on thermal management?
MR CFD Support –
Thank you for your positive feedback! In practical applications, specific materials that can withstand or enhance the magnetic field, such as ferromagnetic materials or soft magnetic composites, may be required, especially for high-intensity fields. Configurations would involve careful placement of magnets or coils and consideration of the overall system’s magnetic permeability. In industries like electronics, automotive, aerospace, etc., efficient thermal management is critical, and the use of nanofluids under a magnetic field could potentially lead to more effective cooling systems, heat exchangers, or even electronic component cooling, translating into enhanced performance and reliability.
Bette Walker –
The simulation’s insightful analysis was great, especially how the external magnetic field influenced the nanofluid behavior. How significant was the impact of the magnetic field, considering the adjusted parameters? Were you able to measure the efficiency change in heat transfer?
MR CFD Support –
Thank you for your compliments on the simulation! The magnetic field notably affected the nanofluid’s thermo-physical properties. By applying a magnetic flux of 1 tesla, we could observe that both fluid dynamics and heat transfer rates within the nanofluid were altered compared to a scenario without magnetic influence. The change in heat transfer efficiency was quantified in our study and reflected in the temperature and velocity contours, showcasing the power of magneto-hydrodynamic control over nanofluid behavior.
Eda Larkin –
This was a super interesting topic! I’m particularly impressed by the detailed analysis of the magnetic field’s effect on nanofluid behavior. It’s fascinating how the presence of a magnetic field can influence the thermal conductivity and overall heat transfer characteristics of the fluid.
MR CFD Support –
Thank you for your positive feedback! We’re glad to hear that you found the topic of magnetic field interaction with nanofluid behavior engaging and that our CFD simulation could provide detailed insights. The intersection of magnetohydrodynamics and nanotechnology presents intriguing opportunities for innovation, and we’re excited to deliver training that explores these advanced concepts through practical analysis. If you have any more questions or need further simulations to supplement your understanding, don’t hesitate to reach out!
Miss Oma Auer Jr. –
I’m amazed by the detailed explanation provided. What impresses me most is the application of the magnetic hydro-dynamic model to see the effect on heat transfer.
MR CFD Support –
Thank you for your kind words! We’re glad you appreciated the comprehensive details and the use of complex modelling in our CFD simulation. Understanding the impact of the magnetic field on nanofluid behaviour is critical for advancing in fields like enhancing heat transfer. If there’s any aspect of the simulation you’d like to learn more about, feel free to reach out!
Amber Lueilwitz –
I was amazed by the detail in your simulation of the magnetic field effect on nanofluid flow! Was it challenging to simulate the interaction between the nanofluid and the magnetic field using ANSYS Fluent?
MR CFD Support –
Thank you for your kind words! We appreciate that you highlighted the detailed approach to our simulation. Simulating the interaction between the nanofluid and the magnetic field did present challenges due to the complexities of magnetic hydro-dynamics and nanoscale particles. However, using the advanced capabilities of ANSYS Fluent and our expertise in CFD analysis, we meticulously addressed the challenges to obtain accurate and detailed results on the effect of magnetic fields on nanofluid behavior and heat transfer.
Prof. Riley Veum –
I am very interested to know how the simulation actually demonstrates the impact of the magnetic field on the heat transfer enhancement. Can you explain this effect with some results?
MR CFD Support –
The simulation showcases the impact of the magnetic field on heat transfer enhancement in nanofluids by demonstrating changes in fluid flow and temperature distribution. Within the magnetic field, the movement of the nanofluid particles changes due to the Lorenz force, which can lead to altered thermal conductivity and convective heat transfer rates. Thus, the contours of temperature and velocity provide insights into how the magnetic field influences the overall heat transfer efficiency of the nanofluid. The increase in thermal conductivity and alterations to flow patterns in the presence of a magnetic field contribute to the heat transfer enhancement, as illustrated in the results of the simulation.
Shayne Turcotte DDS –
I learned so much about nanofluids and the impact of magnetic fields through this course! The visualization of the temperature and velocity profiles was especially helpful for understanding the concepts.
MR CFD Support –
We’re thrilled to hear that our course helped enhance your understanding of nanofluids and the influence of magnetic fields on their behavior. The team takes great pride in producing high-quality visual content to aid learning. Thank you for your positive feedback!
Jayne Heidenreich –
The learning material was top-quality, and the concepts about the MHD model and nanofluids were explained clearly. Understanding the impact of the magnetic field on the nanofluid flow was fascinating. The contour plot analysis provided valuable insight into how the field influences temperature and velocity profiles.
MR CFD Support –
We appreciate your feedback! It’s fantastic to hear you gained valuable insights from the simulation project. We strive to offer clear and thorough training, and we’re glad the contour plot analysis contributed to your understanding of magnetic field effects on nanofluids.
Alessandro Glover DDS –
The integration of CFD and MHD in the simulation is brilliant. I’m particularly impressed with the comprehensive approach towards investigating the nanofluid behavior under a magnetic field. Well done!
MR CFD Support –
Thank you for your kind words! It’s great to hear that you’re impressed with the combination of CFD analysis and MHD modeling to explore nanofluid dynamics. We strive to deliver detailed and accurate simulations to aid in understanding complex phenomena. Your appreciation means a lot to us.
Dr. Billy Schaefer –
Fantastic learning resource! The step-by-step process to simulate the impact of a magnetic field on nanofluid was extremely informative. The material was well-presented, making the complex physics behind MHD and nanofluid behavior very approachable. Can’t wait to apply these concepts in my own simulations.
MR CFD Support –
Thank you for your kind words! We’re thrilled to hear that our ANSYS Fluent training on the effect of magnetic fields on nanofluid was helpful for you. It’s great to know that you found the materials comprehensive and easy to understand. Best wishes on applying these simulations to your work!
Minerva Mueller –
Amazing results. Learned a lot about the influence of magnetic fields on nanofluid behavior in thermal applications. Cheers for the incredibly detailed layout and clarity of the simulation process.
MR CFD Support –
Thank you for your kind words! We’re thrilled to hear that our simulation was informative and helpful in understanding the complex behaviors of nanofluids under magnetic fields. We always strive to provide clear and detailed analyses. Your feedback is greatly appreciated!