Magnetic Field Effect on Nanofluid Heat Transfer (MHD)
$210.00 Student Discount
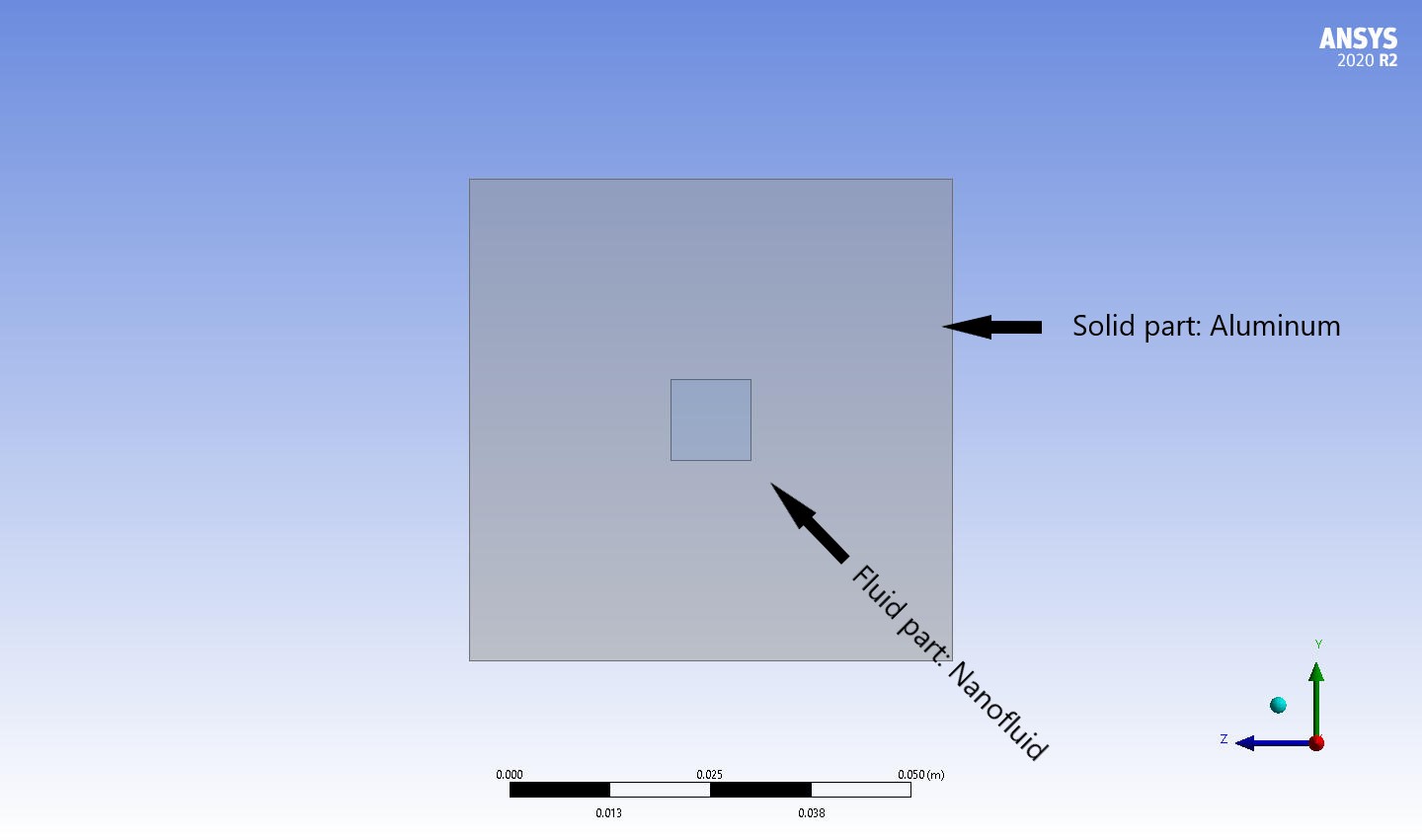
In this project, nanofluid flows in a solid aluminum channel in the presence of an applied magnetic field.
Click on Add To Cart and obtain the Geometry file, Mesh file, and a Comprehensive ANSYS Fluent Training Video.To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Magnetic Field Effect on Nanofluid Heat Transfer (MHD), ANSYS Fluent CFD Simulation Training (3-D)
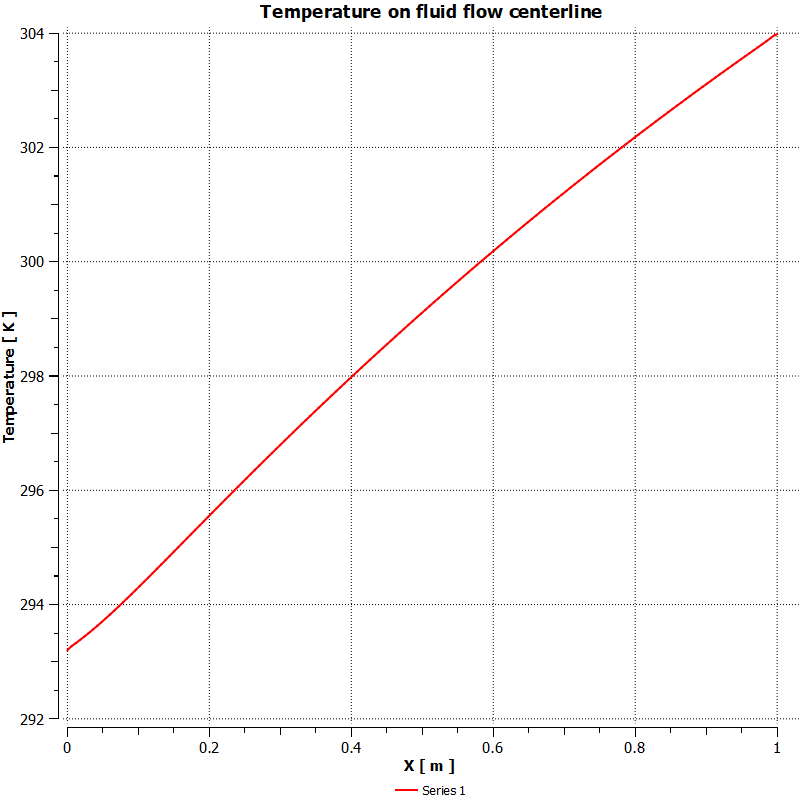
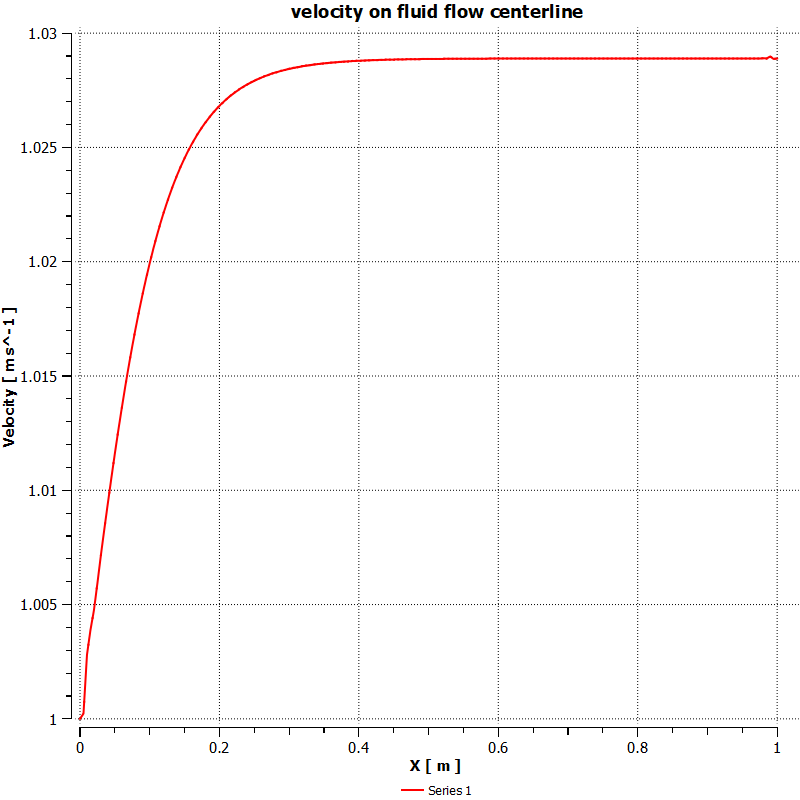
In this project, nanofluid flows in a solid aluminum channel in the presence of an applied magnetic field are simulated by ANSYS Fluent software. Fluid flow is steady and is simulated as one single-phase flow, however, the thermophysical properties of nanofluid are calculated using the below formulas. The surface average of the nanofluid’s temperature is equal to 293.2 and 304.175K at the inlet and outlet, respectively.
where are density, viscosity, specific heat, and thermal conductivity coefficient of nano-fluid and volume fraction of nano-particles in fluid.
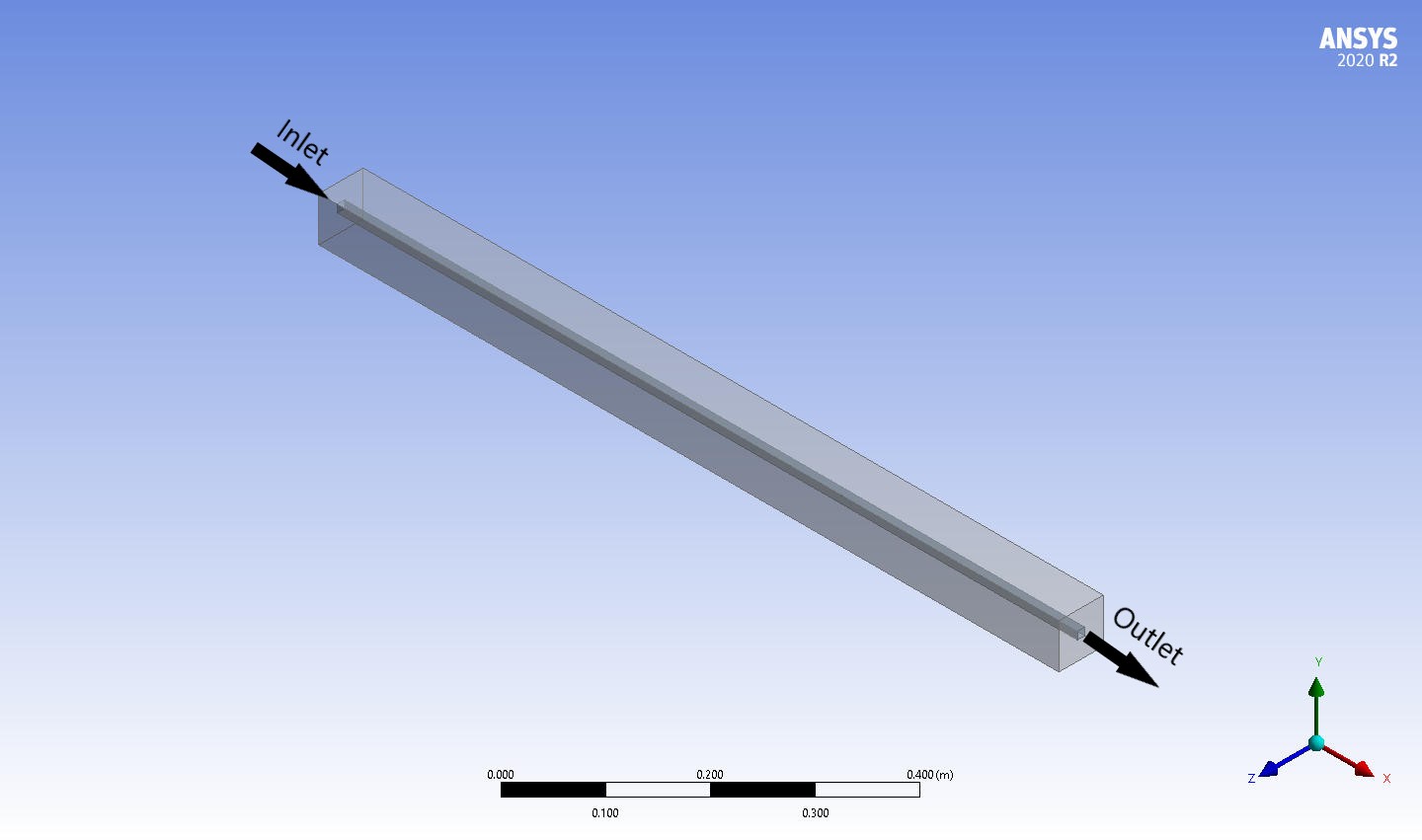
Geometry and mesh
The geometry of the fluid domain is designed in Design Modeler and the computational grid is generated using Ansys Meshing. The mesh type is unstructured and the element number is 26000.
CFD Simulation
Critical assumptions:
- The solver type is assumed Pressure Based.
- Time formulation is assumed Steady.
- Gravity effects are neglected.
The following table is a summary of the defining steps of the problem and its solution.
Solver configurationModels |
||
| Energy | On | |
| Viscous | K-epsilon (standard) | Standard wall function |
| MHD model | MHD method | Magnetic induction |
| Solution control | Solve MHD equation (on) | |
| Include Lorentz force (on) | ||
| Include Joule heating (on) | ||
| Under relaxation (0.9) | ||
| Boundary condition | Solid outer wall (insulating wall) | |
| Fluid-solid interface (coupled wall) | ||
| External field B0 | B0 input option (patch) | |
| B0 component | Bx amplitude (1T) | |
| By amplitude (0T) | ||
| By amplitude (1T) | ||
Solver configurationMaterials |
||
| Fluid | Definition method | Fluent Database |
| Material name | NanoFluid (based on water, with modification) | |
| Density | 1312 kg/m3 | |
| Specific heat (Cp) | 3248 J/kg.K | |
| Thermal conductivity | 1.09387 w/m.K | |
| Viscosity | 0.0011 kg/m.s | |
| UDS diffusivity | constant | |
| Electrical conductivity | 1000000 siemens/m | |
| Magnetic permeability | 1.257e-6 | |
| Solid | Definition method | Fluent Database |
| Material name | Al (based on Aluminum with modification) | |
| Density | 2719 kg/m3 | |
| Specific heat (Cp) | 871 J/kg.K | |
| Thermal conductivity | 202.4 w/m.K | |
| UDS diffusivity | constant | |
| Electrical conductivity | 3.541e7 siemens/m | |
| Magnetic permeability | 1.257e-6 | |
Solver configurationCell zone conditions |
||
| Fluid | Material name | NanoFluid |
| Source terms | Mass (0) | |
| X momentum (1) | ||
| Y momentum (1) | ||
| Z momentum (1) | ||
| Turbulent kinetic energy (0) | ||
| Turbulent dissipation rate (0) | ||
| Energy (1) | ||
| B_x (1) | ||
| B_y (1) | ||
| B_z (1) | ||
| Solid | Material name | Aluminum |
| Source terms | Energy (2)
1. UDF MHD energy source 2. 1000000 w/m3 |
|
| B_x (1) | ||
| B_y (1) | ||
| B_z (1) | ||
Solver configurationBoundary conditions |
||
| Inlet | Type | Velocity inlet |
| Velocity magnitude | 1 m/s | |
| Turbulence intensity | 5% | |
| Turbulent viscosity ratio | 10 | |
| Temperature | 293.2 K | |
| Outer Wall solid | Temperature | 320 K |
| Solver configurations | ||
| Pressure-velocity coupling | Scheme | SIMPLE |
| Spatial discretization | Gradient | Least square cell-based |
| Pressure | Second order | |
| Momentum | Second order Upwind | |
| Turbulent kinetic energy | First order upwind | |
| Turbulent dissipation rate | First order upwind | |
| Energy | Second order Upwind | |
| B_x | First order upwind | |
| B_y | First order upwind | |
| B_z | First order upwind | |
| Initialization | X velocity | 1 m/s |
| Temperature | 293.2 K | |
Magnetic Field Effect on Nanofluid Heat Transfer Results and discussion
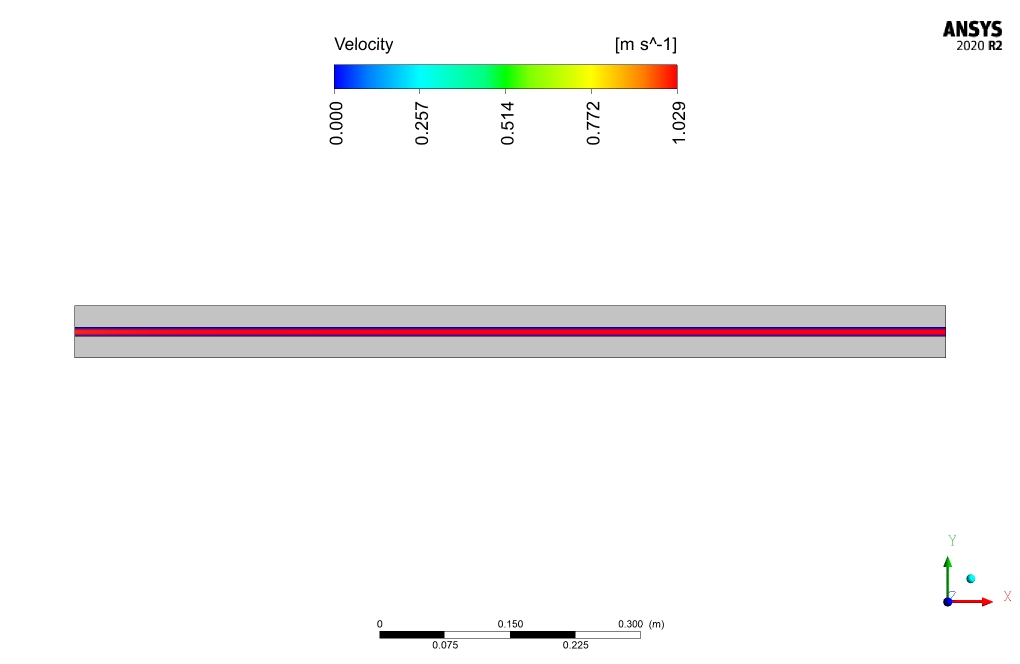
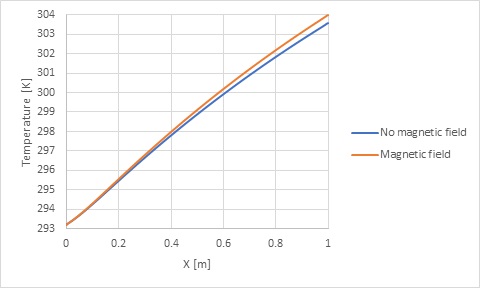
The nanofluid flow average temperature at the inlet and out location is 293.2 and 304.175K respectively. In case of no magnetic field affecting the nano-fluid, the temperature at the outlet decreases to 303.74K. Heat flux to nanofluid is equal to 112102.2 w/m2.
Comparison between outlet temperature of nano-fluid in the presence and absence of magnetic field, reveals the effectiveness of magnetic field application in the present work. Magnetic field application increases outlet temperature by 1K and heat transfer to nano-fluid by 200w/m2.

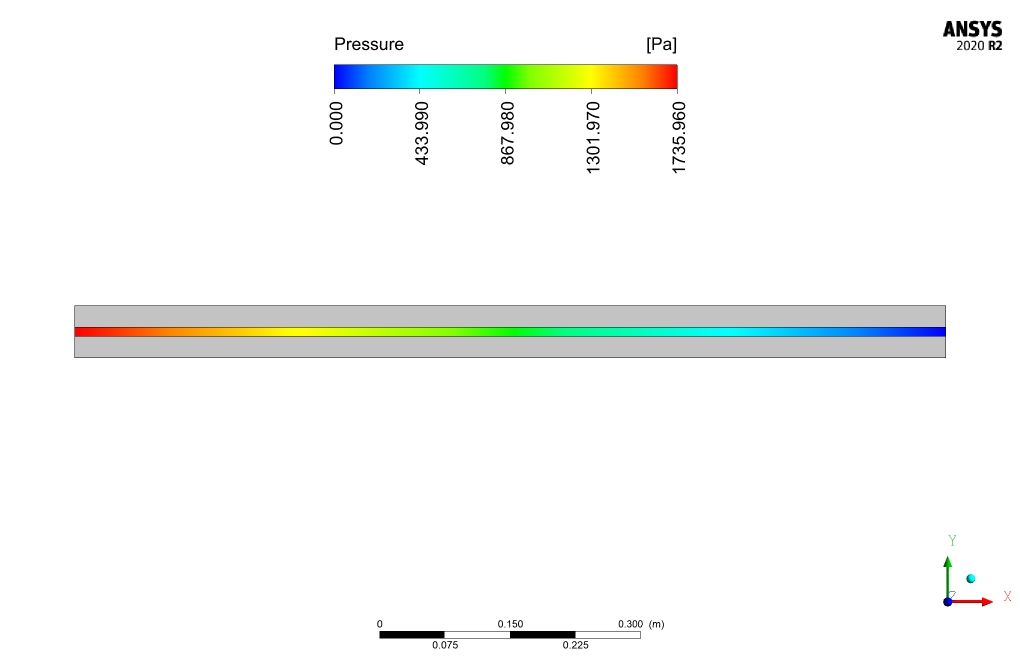

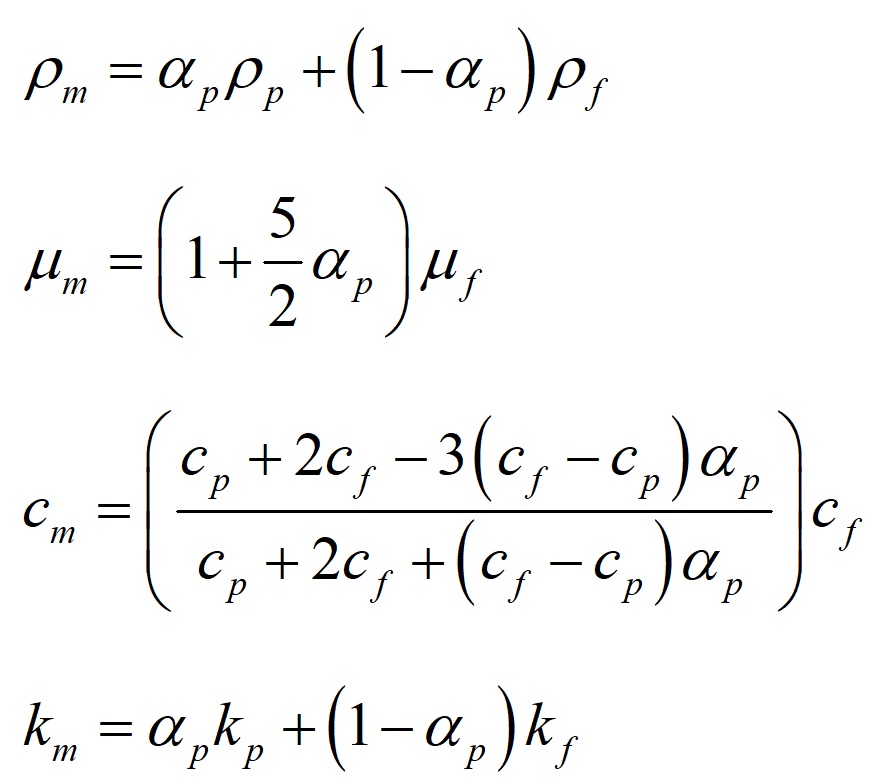


Demond Langosh –
Can this simulation be used to estimate the energy consumption of the heat exchanger?
MR CFD Support –
While the current simulation does not directly estimate the energy consumption, it can provide valuable insights into the pressure drop across the heat exchanger, which can be used to estimate the energy consumption.
Sylvia Waelchi –
Can this simulation be extended to model transient heat transfer scenarios?
MR CFD Support –
Yes, this simulation can be extended to model transient heat transfer scenarios. We are open to contributions and can accommodate your desired simulations.
Gilbert Gibson DVM –
Wow, this training session seems thoroughly insightful and detailed. The results clearly display the effect of a magnetic field on the heat transfer of the nanofluid. This could prove immensely valuable in real-life applications.
MR CFD Support –
Thank you for your positive feedback. We’re pleased to hear that the training session met your expectations and provided valuable insights into the impact of magnetic fields on nanofluid heat transfer. If you have any further questions or need assistance in the future, please don’t hesitate to reach out to us.
Marlin Bernhard –
Just finished going through the Magnetic Field Effect on Nanofluid Heat Transfer (MHD) course. The provided explanation on the impact of a magnetic field on the heat transfer was insightful. Learning about the Lorentz force and Joule heating effects in conjunction with magnetic fields has broadened my understanding of MHD in nanofluid flow within solid channels. I found the simulation results particularly impressive—seeing how the application of a magnetic field can enhance the heat transfer effectively. Excellent training material overall.
MR CFD Support –
Thank you for your wonderful feedback on our Magnetic Field Effect on Nanofluid Heat Transfer (MHD) course! We’re thrilled to hear that the training material was comprehensive and insightful for you and that you were impressed by the simulation results. It’s fantastic to know that we could help broaden your understanding of MHD in nanofluid flows. We appreciate you taking the time to share your experience, and we hope that you’ll find our other training materials just as beneficial.
Ward Luettgen –
How does the simulation model the pressure drop across the heat exchanger?
MR CFD Support –
The simulation models the pressure drop across the heat exchanger using the momentum equations, which capture the resistance to the flow caused by the heat exchanger.
Miss Charlotte DuBuque V –
Can this simulation be used to predict the performance of the heat exchanger at different operating conditions?
MR CFD Support –
Yes, the simulation can be used to predict the performance of the heat exchanger at different operating conditions. This is an important capability for the design and analysis of heat exchangers.
Mr. Brook Yundt –
I am truly in awe of the detailed simulation and training provided for the Magnetic Field Effect on Nanofluid Heat Transfer in ANSYS Fluent. The incorporation of the MHD model adds significant value to the learning experience, ensuring a comprehensive understanding of how magnetic fields influence nano-fluid dynamics and heat transfer. It’s impressive to see results on how the magnetic field increases the outlet temperature and how it intensifies the heat transfer process. Excellent work on designing such an insightful and technical project!
MR CFD Support –
We are so grateful for your positive review! It’s rewarding to know that the details and complexity of the Magnetic Field Effect on Nanofluid Heat Transfer simulation have provided a valuable learning experience. Our goal is to offer in-depth knowledge that can be both educational and practical for our customers. Thank you for acknowledging the effort put into this ANSYS Fluent training module. Your appreciation truly means a lot to us!
Craig Koss –
I’m fascinated by the impact of a magnetic field on nanofluid heat transfer. Could you clarify if non-isotropic materials were considered in the simulation and how the magnetic field exactly enhances heat transfer?
MR CFD Support –
In this simulation, the nanofluid and aluminum channel are assumed isotropic, meaning their properties are uniform in all directions. The application of a magnetic field, known as magnetohydrodynamics (MHD), can influence the movement and energy exchange of the charged particles within the nanofluid. By affecting the fluid motion and creating different flow patterns, a magnetic field can enhance the heat transfer rate. This is demonstrated by the increase in outlet temperature and heat input to the nanofluid when the magnetic field is present.
Manuela Jenkins –
I’m very impressed with how the Magnetic Field Effect on Nanofluid Heat Transfer (MHD) simulation worked! The detailing of how the nanofluid interacted within a magnetic field really gave me a comprehensive view of Heat Transfer phenomena.
MR CFD Support –
Thank you for your positive feedback! We’re thrilled to hear that our simulation product gave you a clear understanding of heat transfer processes in nanofluids within a magnetic field. Your satisfaction with the details and comprehensive view offered by our simulation is our greatest goal. Should you have any further interest in exploring related topics or have any questions, don’t hesitate to reach out.
Josie Feest –
I was impressed with the level of detail and organization in your report on the Magnetic Field Effect on Nanofluid Heat Transfer (MHD). The step-by-step explanation of the solver configuration and boundary conditions is commendable. This clarity helps in understanding how the magnetic field influences nanofluid heat transfer within the channel.
MR CFD Support –
Thank you very much! We appreciate your positive feedback on our training material. Our goal is always to provide a comprehensive guide that can be of help to both beginners and experts in the field of CFD. We’re thrilled that you found our report on the Magnetic Field Effect on Nanofluid Heat Transfer to be clear and informative!