Plastic Cover Effect in Banks Regarding COVID-19, ANSYS Fluent Simulation
$180.00 Student Discount
- The problem numerically simulates virus particles’ release from a patient’s mouth inside a bank using ANSYS Fluent software.
- This project is performed in two modes: with and without the plastic cover.
- We design the 3-D model by the Design Modeler software.
- We Mesh the model by ANSYS Meshing software, and the element number equals 1570219 and 1618366, respectively.
- We perform this simulation as unsteady (Transient).
- We use the discrete phase model (DPM) to define virus particles dispersed from the mouth.
- We define an Injection as the Droplet which is evaporated.
- We use the Species Transport model to define evaporating gas species.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Description
In this project, based on the CFD method and using ANSYS Fluent software, an attempt has been made to simulate virus particles’ release from a patient’s mouth inside a bank. We perform this CFD project and investigate it by CFD analysis.
The present model is designed in three dimensions using Design Modeler software.
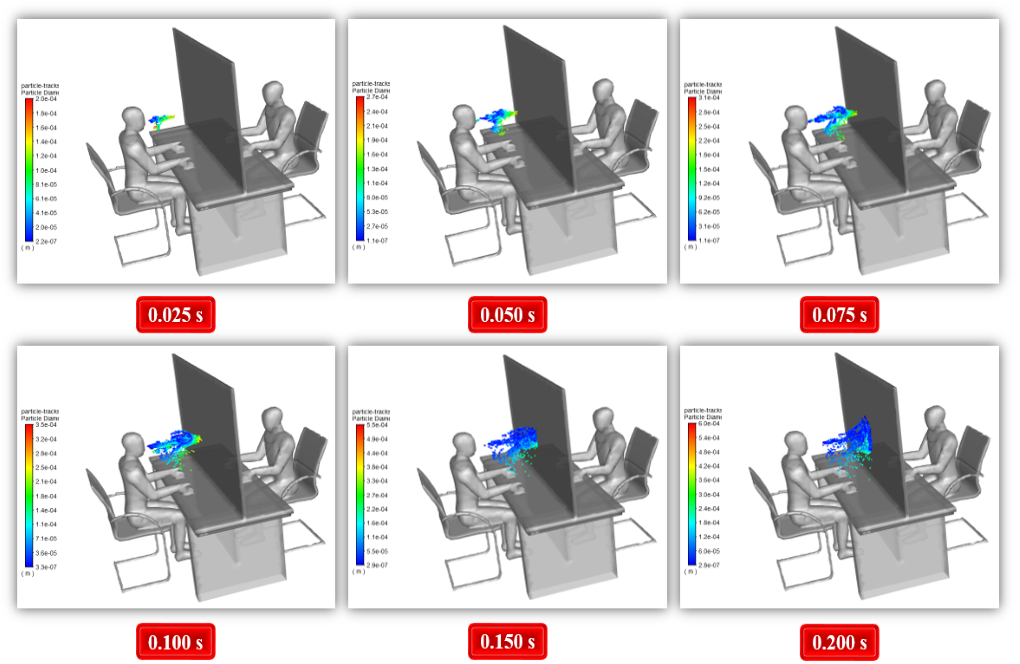
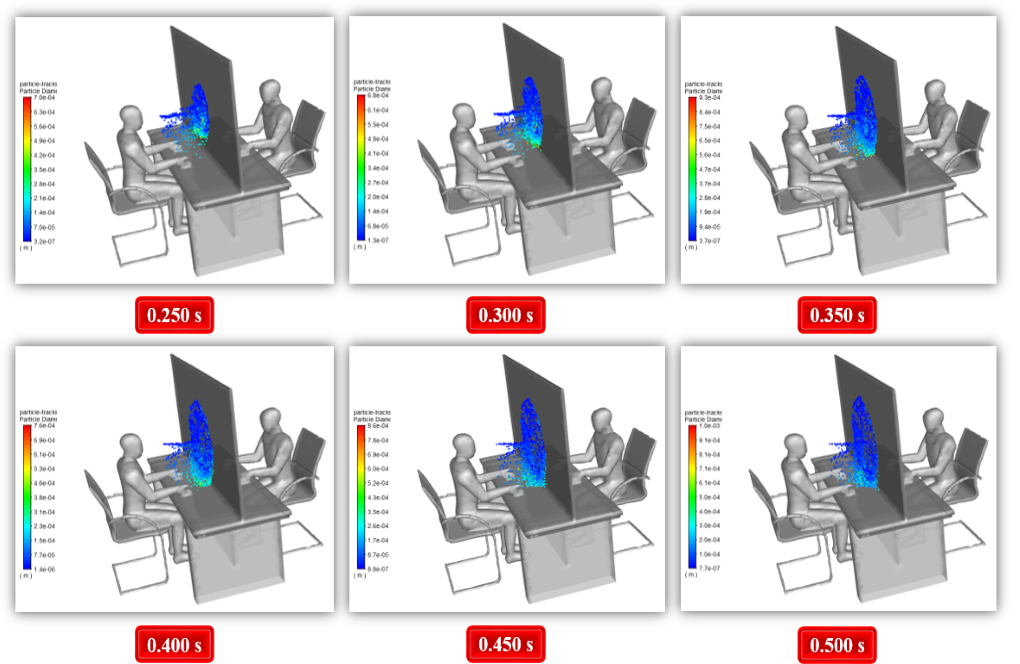
The model’s geometry includes a computational domain of the interior of a bank that includes a table, two chairs, and two people. In this modeling, one of the two humans is a sick person. We defined him as the virus’s source via cough.
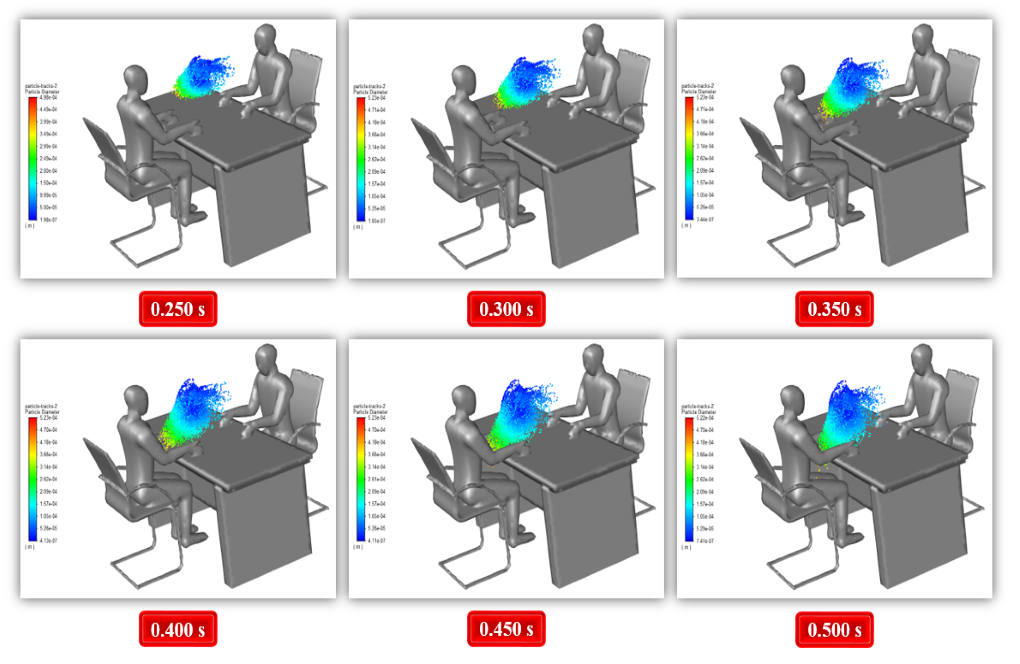
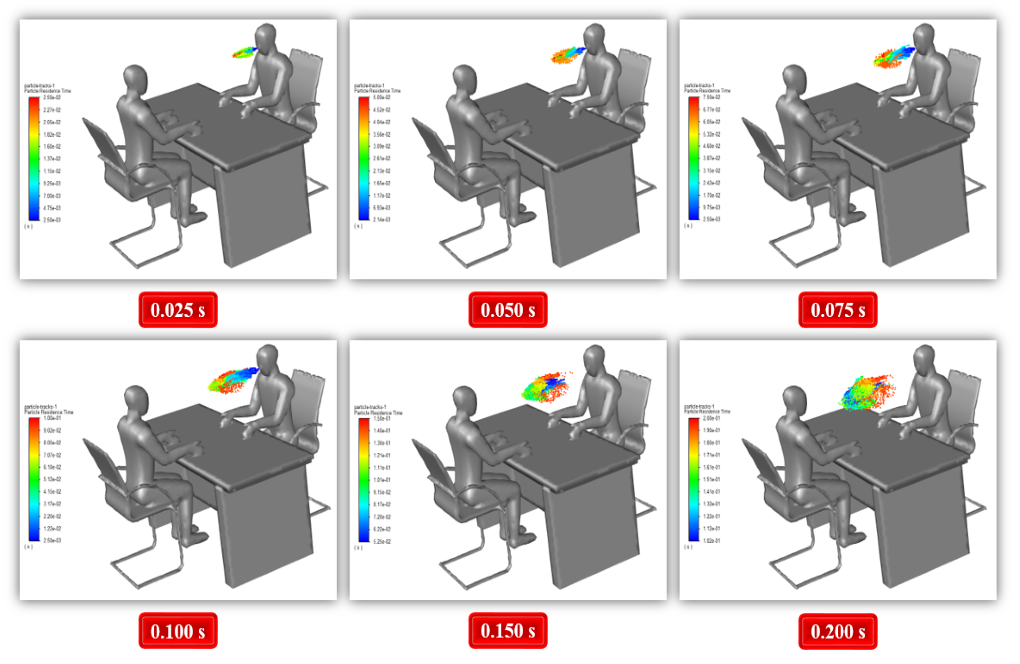
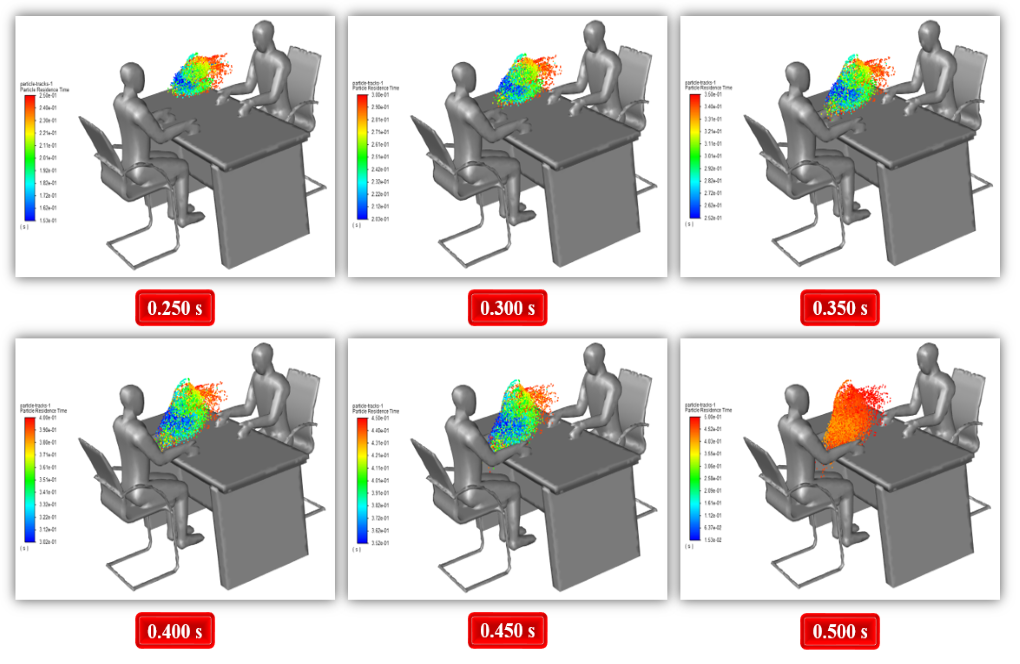
This model assumes the mouth as the reference surface of the discrete phase virus release. In this simulation, two different geometric models are designed, including a case with no plastic cover and another case considering a thin plastic cover between two people on the table.
The meshing of the model has been done using ANSYS Meshing software. The element numbers are 1570219 and 1618366 for the first case (without plastic cover) and the second case (considering plastic cover), respectively.
Also, a transient solver has been used due to the nature of the project (i.e., particle/virus dispersion).
Plastic Cover Methodology
This study investigates coronavirus particles’ ability to spread inside the bank from a bank customer to a healthy bank employee. This simulation process is performed in two different modes.
In the first modeling, no cover is located between the client and the bank employee to show the virus’s transmission power. In the second model, an attempt is made to make a thin plastic cover between them.
The cover should be defined to demonstrate the process of preventing the transmission of virus particles as a barrier. For the present simulation, the discrete phase model (DPM) is used; Because this model allows us to study a mass of particles discretely or bit by bit in a continuously fluid space.
The physical models of discrete particles defined in this simulation include two-way turbulence coupling, meaning two-way interaction between continuous and discrete phases activating the interaction with continuous phase mode.
Stochastic collision means irregular droplets colliding with each other, coalescence means droplets merging, and breakup implies the droplets’ collapse. The type of discrete phase behavior will also be time-dependent and with a time step of 0.001 s (activating the unsteady particle tracking mode).
After activating the discrete phase model, the injection process must be defined, determining the type and quality of discrete particles injected into the model. In this model, injection particles are defined as Droplets; Thus, water is defined as droplets, and water vapor is defined as an evaporating gas species.
The injection is performed superficially and through the Surface of the patient’s mouth. According to this definition of injection, virus particles from a sick human cough are physically expelled from the patient’s mouth by water droplets evaporating in space.
These virus droplets have a temperature of 310 K, a velocity of 32 m/s, and a flow rate of 0.018 kg/s, emitted at intervals of 0 s to 0.1 s.
The virus particle size during propagation is not constant, and the rosin-rammler-logarithmic distribution method is considered for the diameter’s size.
Following this method and the suitable formulation, the values related to the minimum, maximum and average diameter size determine the exponential parameter of the spread and the number of diameters per injection.
It should be noted that the Droplet mode is applied when the species transport model is also activated. In this model, three different gases, including oxygen (O2), nitrogen (N2), and water vapor (H2O), are considered, and thus the computational area of our model will have airflow.
Also, the RNG k-epsilon model and energy equation are enabled to solve the turbulent fluid equations and calculate the temperature distribution inside the domain.
Plastic Cover Conclusion
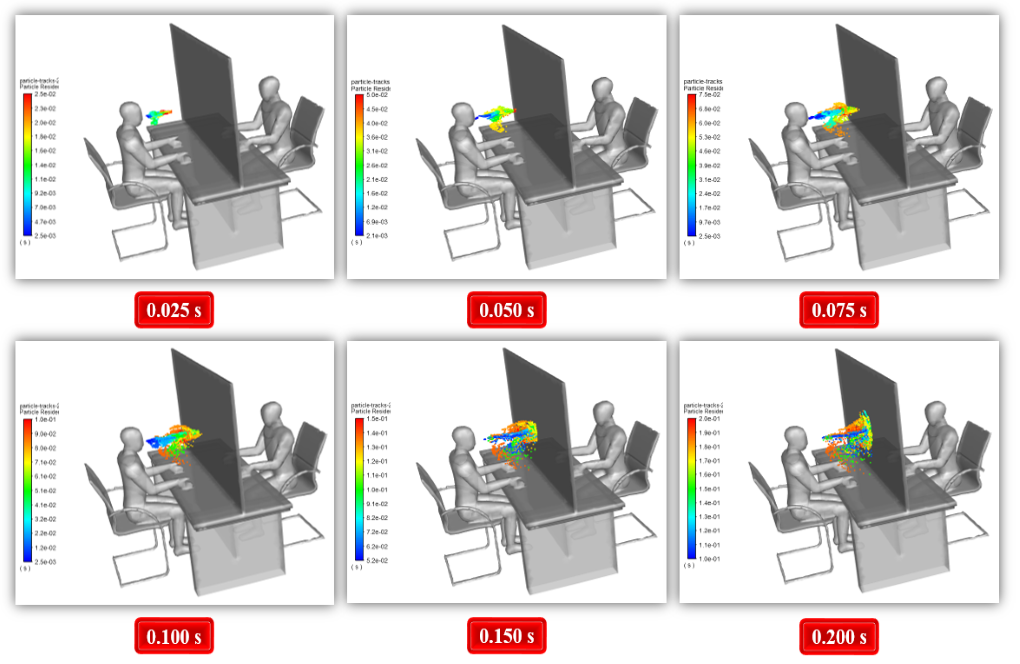
At the end of the solution process, we obtain particle tracking of the virus particles at different time intervals of the simulation process. This particle sequence is based on the residence time of the particles and the particle diameter size.
We perform this simulation process in two modes, with and without the plastic cover. The effect of plastic cover in preventing coronavirus dispersion is evident from the results, demonstrating how the modeled cover can prevent the spread of the virus.
Reviews
Related products
-
Non Newtonian Blood Pulse Flow in a Vein, ANSYS Fluent CFD Training
Rated 4.75 out of 5$120.00 Student Discount -




Prof. Santos Stanton DDS –
The simulation comparison of virus spread with and without the plastic cover is brilliant. It really showcases the effectiveness of simple barriers in infection control.
MR CFD Support –
Thank you for the compliment! We’re delighted to hear that our simulation provided clear insights into the importance of protective measures. If you have any further questions or need additional information on our simulations, feel free to ask. We’re here to help!
Prof. Marion Simonis –
I’ve just completed my simulation project on the dispersion of virus particles and was impressed with the clarity of the modeled spread. Seeing how protective barriers function was fascinating. Well done!
MR CFD Support –
Thank you for your positive feedback! We’re thrilled to hear that the simulation was clear and informative, and that you found the visualization of protective barriers and their functionality insightful. Your satisfaction with the results is very important to us. If you ever have more questions or need further assistance for your future projects, feel free to reach out!
Diana Stoltenberg –
What were the specific benefits observed with the plastic cover in the simulation?
MR CFD Support –
The simulation showed that the plastic cover effectively prevents the spread of virus particles by acting as a barrier. It significantly reduced the number of virus particles transmitted between the client and the bank employee, indicating its potential to curb the transmission of infections like COVID-19 in indoor public spaces such as banks.
Prof. Bell Harris –
The study is truly intriguing! Could you clarify how the plastic cover’s effectiveness was assessed in the simulation, particularly regarding the virus particles’ dispersion?
MR CFD Support –
In the simulation, two scenarios were compared: without a plastic cover and with a plastic cover. The effectiveness of the plastic cover was assessed by tracking virus particle dispersion in both scenarios. In the case with the plastic cover, the model evaluated how the cover acted as a barrier restricting the transmission of virus particles from the infected person to the healthy bank employee. The discrete phase model (DPM) allowed for observing the behavior and interaction of the particles with the plastic cover, providing a visual representation and quantitative data on the particles’ spread and the cover’s effectiveness.
Dedric Hartmann Sr. –
I am impressed by the detailed approach to visualizing how the coronavirus particles move with and without the plastic cover. The application of discrete phase modeling in this context is really insightful.
MR CFD Support –
Thank you for your positive feedback! We’re glad that you found the use of the discrete phase model in visualizing virus particle movement to be valuable. We strive to provide detailed and insightful simulations to aid in understanding complex fluid dynamics, especially in relevant health and safety scenarios.
Jamaal Von –
I’m so impressed by the modeling detail in this CFD project regarding simulations of real-world public health situations. The use of ANSYS Fluent to analyze virus particle spread in a bank setting is a powerful demonstration of utilizing technology for safeguarding environments against airborne threats. Great job at balancing computational rigor with meaningful insights.
MR CFD Support –
Thank you for your positive feedback! We appreciate your acknowledgement of the details involved in this simulation project. MR CFD takes pride in using the latest technology for meaningful and impactful research. If you have any more thoughts or need further information about our simulations and other services, feel free to reach out.
Anahi Sauer –
I was fascinated by the study on the effectiveness of plastic covers in banks. Can you explain further how the cover impacts virus particle behavior compared to when there is no cover present? Does it show any disturbance in airflow that could affect virus transmission?
MR CFD Support –
The plastic cover acts as a physical barrier that prevents the droplets containing the virus particles from directly reaching the bank employee. When no cover is present, the virus particles can travel freely by following the airflow, potentially reaching the healthy individual. The presence of the cover changes the airflow pattern, causing a disturbance that redirects the airflow. This disruption helps to reduce the number of particles that can reach the other side of the cover. The simulation compares two scenarios—one with and one without the plastic cover—showing how the tailored use of the cover diminishes the likelihood of virus transmission due to altered airflow and particle trajectories.
Luz Beatty –
I found the details of the methods on virus particle distribution very comprehensive. How effective was the plastic cover in preventing the spread compared to having no cover at all based on your results?
MR CFD Support –
Our CFD simulation results clearly demonstrated the efficacy of the plastic cover. When the plastic cover is present, it acts as a barrier and significantly restricts the spread of virus particles from the infected individual to the bank employee, in comparison to the scenario where no cover is used. Therefore, the plastic cover is highly effective in preventing virus dispersion between the two individuals in the bank setting.
Adriana Hill –
Did the simulation show any specific situations in which the plastic cover was less effective, or did it consistently prevent the spread of virus particles regardless of particle size or other variables?
MR CFD Support –
In the simulation, the plastic cover effectively prevents the spread of virus particles in both scenarios, regardless of the size of the particles or other variables. The results demonstrate consistent prevention of virus transmission with the inclusion of the plastic cover barrier.
Alvis Upton –
This product’s details show immense potential for improving safety in banks. I especially appreciate the practical approach towards diverse situations like with and without the plastic cover. Can’t wait to see how this study might inform future designs and safety protocols in public spaces.
MR CFD Support –
Thank you for your kind words! We’re thrilled to hear that our product could contribute to enhancing safety measures. Real-world application and providing actionable insights is a top priority for us, and we hope our simulation outcomes will indeed influence design strategies and improve public health protocols. Stay tuned for more innovative solutions!
Mr. Westley Brekke I –
I found the methodology for the Plastic Cover Effect in Banks study to be very comprehensive. The attention to detail, especially in defining the behavior of virus particles and their interactions, is impressive.
MR CFD Support –
Thank you for your kind compliments on our Plastic Cover Effect in Banks simulation study. We strive to ensure that our CFD analysis is detailed and accurate, and we are glad that the thoroughness of our methodology has been well-received. We appreciate your feedback!
Dawson Maggio II –
The simulation’s results sound impressive! The idea of using a thin plastic cover as a barrier to virus spread is quite ingenious. It’ll be exciting to visualize how this setup has made a difference.
MR CFD Support –
Thank you very much for your compliment! We are pleased to know that our CFD simulation product has met your expectations and provided valuable insights. Visualizing the impact of protective measures like a plastic barrier is indeed essential, and we’re glad we could clearly demonstrate it through the simulation. We’re excited for the opportunity to aid in the understanding of virus transmission and prevention measures.
Garnet Rippin –
Great use of CFD for public health safety! Kudos.
MR CFD Support –
Thank you for the kind words! We’re glad to provide tools that can help visualize and understand complex phenomena such as virus dispersion, contributing to public health safety.
Jeanne Denesik V –
This CFD simulation is fascinating. Does the simulation take into account changes in cough dynamics, such as varying droplet sizes or cough strength?
MR CFD Support –
Yes, the simulation does consider such variations. Droplet size is distributed using the rosin-rammler-logarithmic distribution to account for a range of droplet sizes emerging from a cough. The simulation also defines a specific initial velocity and temperature for the expelled droplets to mimic the dynamics of a cough.
Retta Bogisich Sr. –
The simulation results sound promising! Has the study considered different cough intensities and plastic cover sizes to evaluate the effectiveness more comprehensively?
MR CFD Support –
Thank you for your kind words and interesting question. However, the information provided does not detail varying cough intensities or plastic cover sizes. It solely focuses on the predefined setup mentioned in the description with specific input parameters. For broader analysis, additional simulations with varied conditions would indeed be required.
Reva Block –
I was quite impressed with the level of detail in simulating the effect of the plastic cover in banks for Covid-19. The use of ANSYS Fluent to study the particle behavior and the differences between cases with and without the cover provided great insights. Great work!
MR CFD Support –
Thank you for your review! We’re delighted to hear that you found our simulation detailed and insightful. We strive to provide accurate and comprehensive analyses using ANSYS Fluent, and it’s rewarding to know you appreciate the effort. If you have any further questions or need more information on this or other simulations, don’t hesitate to reach out!
Prof. Stefanie Marquardt –
The simulation was wonderfully detailed and the visual results were impressive! I could really see how the plastic cover impacts virus particle spread.
MR CFD Support –
Thank you for your positive feedback! We’re thrilled to hear the results of the ‘Plastic Cover Effect in Banks Regarding COVID-19’ simulation were clear and informative. Your satisfaction with our product is our highest priority. Should you have any further inquiries or need more details, feel free to reach out.
Theodora Shanahan –
I was impressed with how meticulously the Plastic Cover Effect project replicated the real-world transmission scenario of the virus particles inside a bank setting. The usage of different models to delineate the presence and absence of a plastic cover provided clear insights into the protective measures. The detailed attention paid to vaccine particle temperatures, velocities, and the rosin-rammler-logarithmic distribution for droplet sizes was truly commendable.
MR CFD Support –
Thank you for your positive feedback! We are glad you appreciated the thoroughness and level of detail in our simulation study. It’s always our goal to provide insightful and realistic modeling results that can be informative in practical applications, such as understanding and mitigating virus transmission. Your appreciation motivates us to keep delivering high-quality CFD analyses that meet and exceed expectations.