Corona Virus Spread due to a Cough in Open Air
$160.00 Student Discount
- The problem numerically simulates coronavirus spread due to human cough in the open air using ANSYS Fluent software.
- We design the 3-D model with the Design Modeler software.
- We Mesh the model with ANSYS Meshing software, and the element number equals 584587.
- We perform this simulation as unsteady (Transient).
- We use the Discrete Phase Model (DPM) to define an injection of droplet various.
- We use the Species Transport model to consider evaporating species.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Corona Virus Spread due to a Cough in Open Air, ANSYS Fluent CFD Simulation Training
The present problem aims to simulate coronavirus spread due to human cough in the open air using ANSYS Fluent software.
This spreads the virus particles in the open air and can infect a person at a certain distance from the patient.
Therefore, one of the most up-to-date topics that researchers are constantly researching is calculating and examining the minimum appropriate distance between a sick person and a healthy person to prevent the spread and transmission of viruses when a patient coughs or sneezes, called social distancing or physical distancing.
This model involves a human placed in a cube-shaped computational domain as the open air, and the human mouth is distinguished as a source of virus transmission.
The present 3-D model is designed using SOLIDWORKS and Design Modeler software.
The model meshing has been done using ANSYS Meshing software, and the mesh type is unstructured. The mesh accuracy is higher in areas close to the patient’s mouth than elsewhere. The element number is 584587.
CFD Methodology
This project uses a two-way discrete phase model (DPM). The behavior of discrete phase particles in the unsteady state is also defined, and it is also assumed that the behavior of the particles is affected by the continuous flow (interaction with continuous phase).
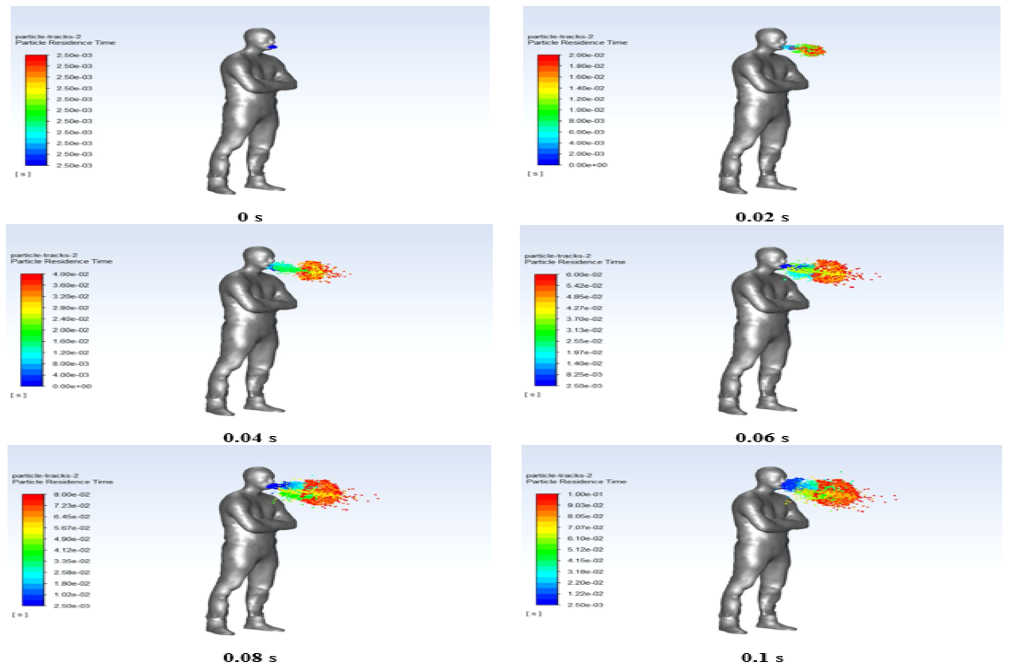
The physical states defined for the discrete phase model include stochastic collision, coalescence, and breakup. These droplets have a temperature of 310 K, a velocity of 31.85 m.s-1, and a flow rate of 0.018 kg.s-1, which are emitted in the interval of 0 s to 0.1 s.
The diameters of these particles are not constant and equal to each other; therefore, the rosin-rammler-logarithmic distribution method is considered for the size of the diameters. Determine the minimum, maximum and middle diameter size, spread parameter and the number of diameters per injection.
It should be noted that the droplet mode is applied when the species model is enabled. In this model, the mode of species transport is activated to simulate the droplet and evaporation; thus, the working space of the model around the patient will have airflow.
According to the definition of injection, virus particles from a human cough are physically expelled from the mouth by water droplets evaporating in space.
Corona Virus Spread Due to a Cough Conclusion
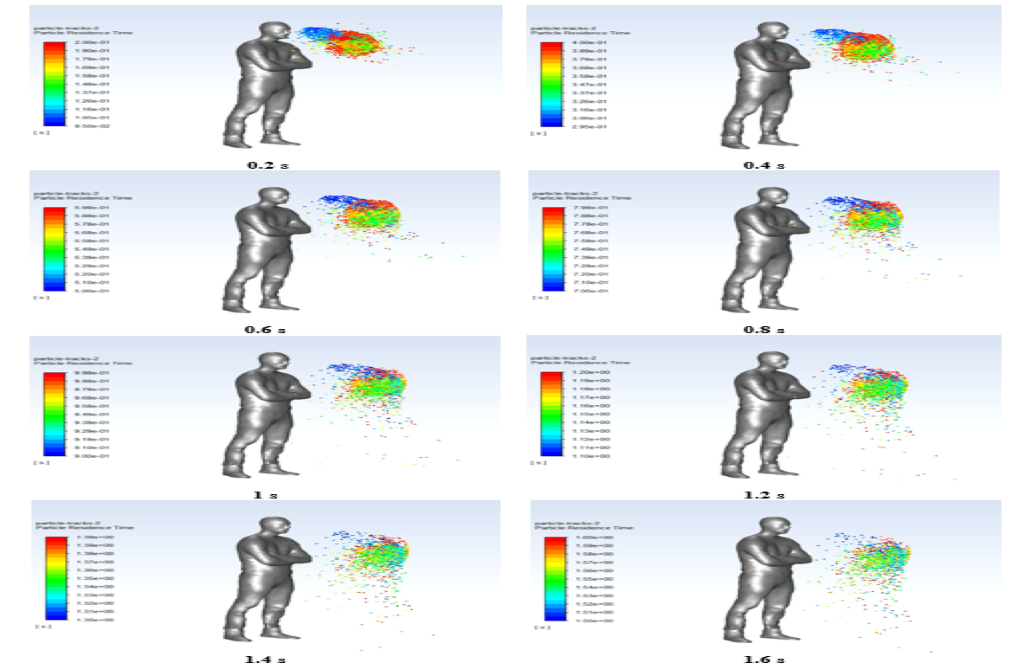
At the end of the solution process, we obtain the particle tracking of the virus particles. This particle sequence is based on the output resistance time. We take out the animation of the virus release and its disappearance over time.
Also, we obtain and present the images related to the virus particle sequence at different times. The results show the virus spread during the patient’s cough, which occurs in the open air from 0.1 s to 1.75 s.

Dr. Lesley Hamill –
The subject of your products is significantly updated.
Vincenza Rosenbaum –
I’m going to solve this product for a 2-way project. Can this product help me?
MR CFD Support –
The physical model of the discrete particles in this product is considered as a two-way DPM. So this training product will be so practical for your 2-way purpose.
Miss Constance Rodriguez –
This simulation is a fantastic tool for understanding the complex transmission dynamics of the coronavirus!
Hollis VonRueden Sr. –
Can I contribute to this simulation?
MR CFD Support –
What is the benefit of using CFD for analyzing the spread of the virus due to a cough?
Alysson Schowalter –
It is a fantastic collection of current subjects.
Thank you, Mr. CFD.
Shaylee Sporer –
I am impressed by the level of detail in this simulation.
Jody Harber –
I am immensely satisfied with how the simulation represents virus particle spread due to coughing in open air. The precision involved in setting up the initial boundary conditions and considering the various aspects of airborne transmission reflects a well-thought-out approach, which can be extremely valuable for public health studies.
MR CFD Support –
We’re thrilled to hear that our simulation met your expectations and you found it insightful! Ensuring accuracy and precision in such important public health simulations is a top priority for us, and we appreciate your positive feedback. Thank you for taking the time to review our product.
Liam Jakubowski –
What measures are in place to ensure realism in the cough simulation and accuracy in determining social distancing guidelines?
MR CFD Support –
In the simulation, realism is achieved by incorporating the discrete phase model (DPM) to simulate virus particle behavior, along with droplet modes that include evaporation. The simulation also considers various droplet sizes distributed according to the rosin-rammler-logarithmic method. These sizes are also coupled with the species transport model to simulate the airflow around the coughing patient accurately. Additionally, the droplets are emitted with realistic temperatures and velocities. Social distancing guidelines can be fine-tuned by analyzing the particle tracking results to determine the range and behavior of virus particles during a cough over time.
Ms. Karlee Shanahan –
Can you please explain how the social/physical distancing factor is determined using this simulation? Sort of unclear to me from the description.
MR CFD Support –
In this simulation, physical distancing is determined by analyzing the spread of virus-laden particles from a cough. We track the particles across time and space and identify how far they travel before settling or evaporating to provide insights into the safe distances individuals should maintain to minimize the risk of virus transmission.
Caleigh Terry –
What surface inside the model would be a likely target for the virus particles spread by a cough, according to the simulation setup?
MR CFD Support –
In this simulation scenario, the most likely target surface for virus particles spread by a cough would be the surfaces directly in front of the patient, within the trajectory of the expelled particles. The area directly opposite the mouth’s release point would receive the highest concentration of viruses due to direct exposure to the initial velocity and dispersion pattern of the cough.
Carmine Thompson –
Which factors are considered to impact the spread of virus particles in this simulation?
MR CFD Support –
In this simulation, the factors considered for the impact on virus particle spread include the velocity and temperature of the cough droplets, the flow rate of the cough, the size and distribution of the droplets, the ambient airflow, and the evaporation process. Moreover, the discrete phase model accounts for interactions between the particles and the continuous phase, as well as stochastic collision, coalescence, and breakup of droplets.
Prof. Dante Champlin DVM –
The simulation provided excellent insights into the dynamics of virus spread due to a cough. Fantastic work visualizing something so crucial for public health during such times as a pandemic.
MR CFD Support –
Thank you for your positive feedback! We’re pleased to hear that the simulation was informative and helpful in understanding the important aspect of virus transmission through coughing. Our team strives to create simulations that are not only accurate but also valuable for educational and research purposes.