Radiator Transient Heat Transfer in a Room Simulation
$100.00 Student Discount
- The problem numerically simulates Radiator Transient Heat Transfer in Room using ANSYS Fluent software.
- We design the 3-D model by the Design Modeler software.
- We Mesh the model by ANSYS Meshing software, and the element number equals 4148881.
- We perform this simulation as unsteady (Transient).
- The Energy Equation is activated to consider heat transfer.
Click on Add To Cart and obtain the Geometry file, Mesh file, and a Comprehensive ANSYS Fluent Training Video.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Radiator Transient Heat Transfer in Room, ANSYS Fluent CFD Training
The problem is simulating heat transfer by a Radiator inside a room by ANSYS Fluent software. We perform this CFD project and investigate it by CFD analysis.
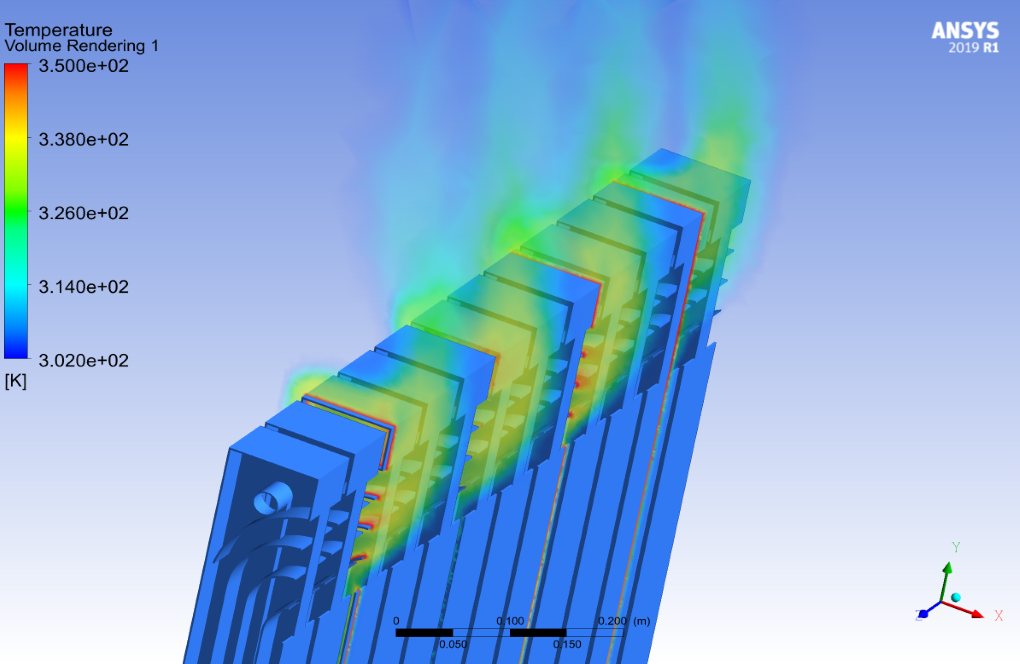
The radiator is attached to a sidewall, which is a heat source. The radiator consists of hot water flow pipes and aluminum fins. It is assumed that the hot water flow inside the pipes has a constant temperature. As a result, the body of the pipes has a constant temperature equal to 353 K.
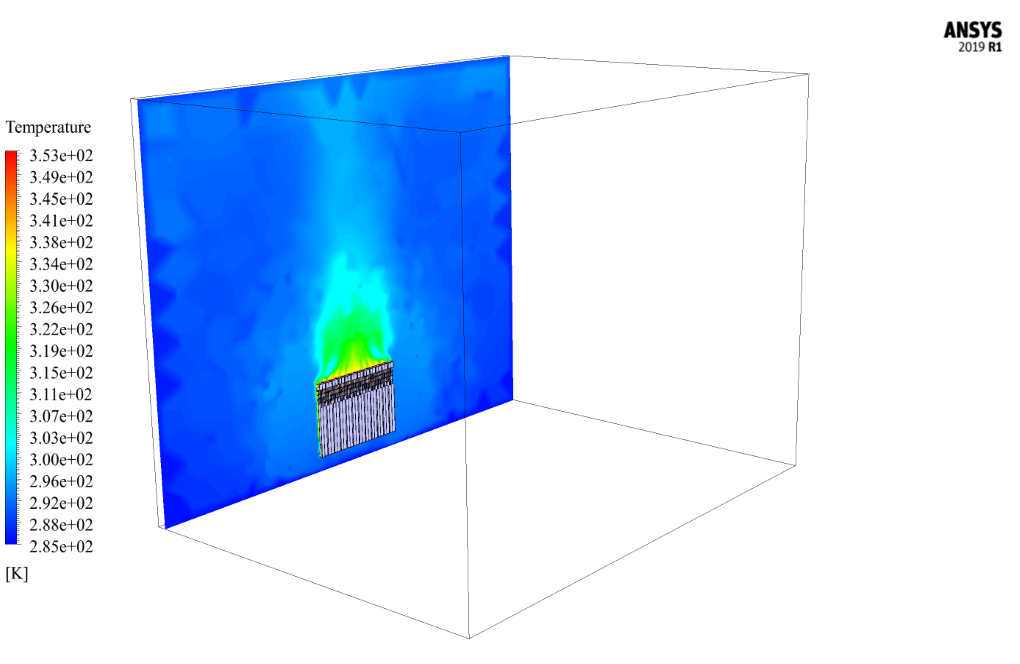
The walls of the room have a thickness of 0.3 m, which has convection heat transfer with the outside; Thus, the ambient air temperature is assumed to be 284 K, and the convection heat transfer coefficient is considered to be 8 W/m2K.
Radiator in Room Methodology
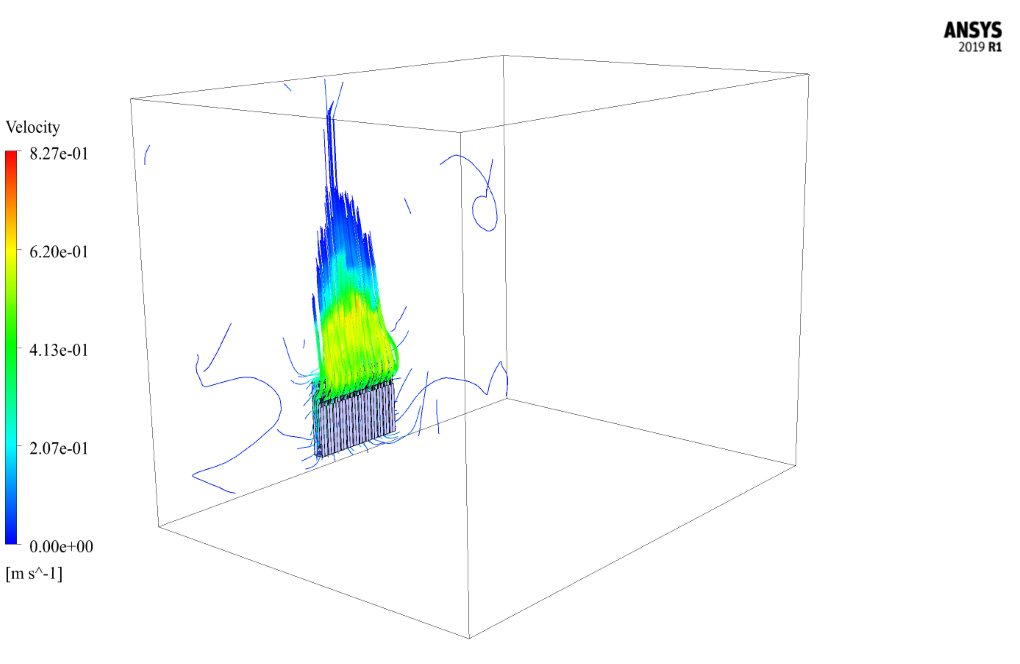
The gravity effect is applied to the model. Also, The simulation is transient.
The present 3-D model is drawn utilizing the Design Modeler software. The current model consists of a room in the shape of a rectangular cube with dimensions of 4 m * 3 m * 3 m, and a radiator inside is connected to one of its sidewalls.
The model meshing has been done using ANSYS Meshing software, and the mesh type is unstructured. The element number is 4148881.
Radiator in Room Conclusion
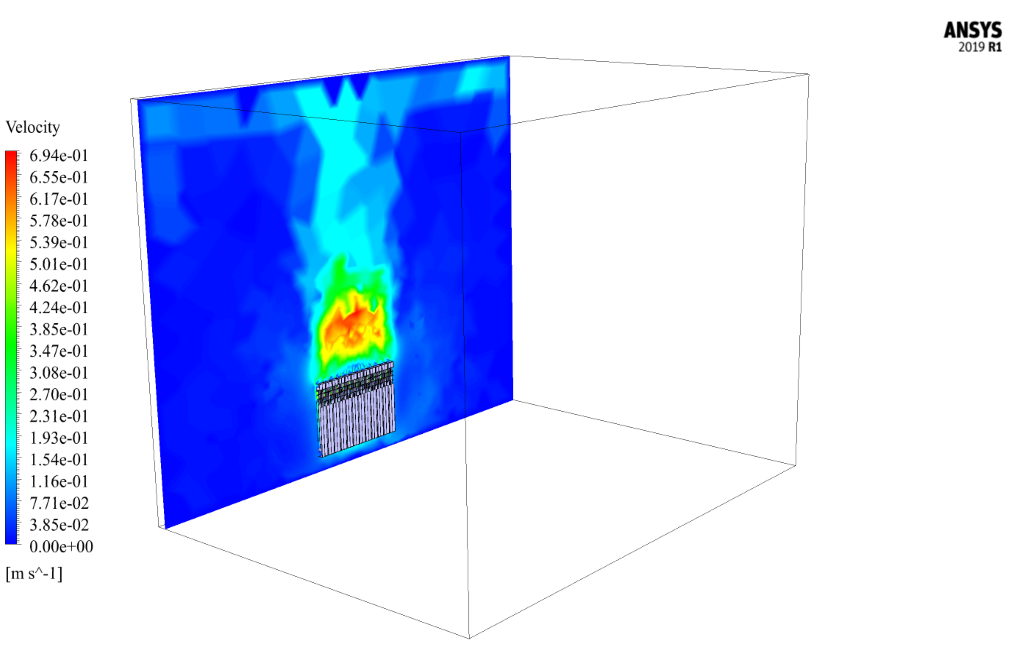
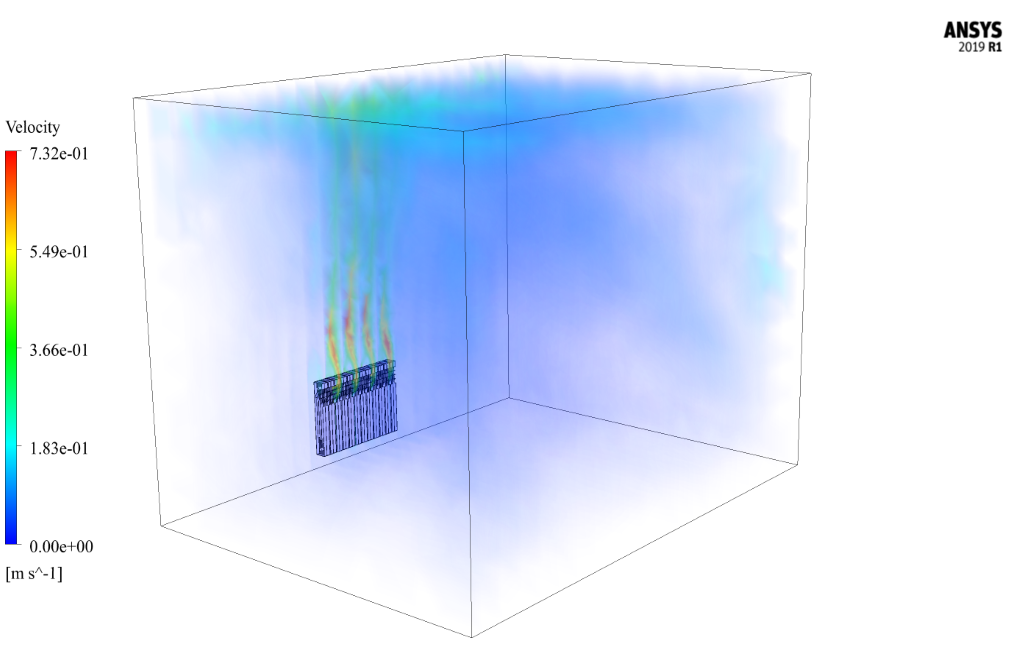
The purpose of this study is to investigate the heat transfer rate from the radiator to the room’s interior using natural convection and the buoyancy effect. By analyzing the temperature contours, we can easily find the heat transfer in the room space by applying the radiator as a function of time.






Miss Jude Erdman –
Hi, can you send me the radiator design?
MR CFD Support –
Hi, my friend
you can go to the following link:
http://www.mr-cfd.com/shop/radiator-heat-transfer-inside-a-room-transient-cfd-simulation
Damian Hilpert –
Does the simulation consider the effects of different ambient temperatures?
MR CFD Support –
Absolutely, the simulation accurately captures the effects of different ambient temperatures on heat transfer.
Dorthy Gleason –
Does the simulation consider the effects of different radiator flow rates?
MR CFD Support –
Yes, the simulation accurately captures the effects of different radiator flow rates on heat transfer.
Ms. Autumn O’Conner II –
I just completed the ‘Radiator Transient Heat Transfer in a Room Simulation’ course, and I’m blown away by how it vividly explains the radiator-heat interaction in a living space. The course content was in-depth and easy to understand with precise instructions for setting up the simulation. The results truly reflected the transient nature of heat distribution, and the setup of the constant temperature for the water flow in pipes demystified complexity. A fantastic tool for anyone seeking clarity on heating system integrations!
MR CFD Support –
We are delighted to hear that you are satisfied with your learning experience from the ‘Radiator Transient Heat Transfer in a Room Simulation’ course! It’s great to know that the material was beneficial and straightforward for you to use. We always strive to deliver high-quality content that can simplify complex concepts for our learners. Thank you for taking the time to give us your positive feedback. If you ever have any questions or need further assistance in your learning journey, feel free to reach out!
Bernardo Deckow –
I’m very impressed by the realistic setup of the transient simulation! Could you tell me, from the simulation results, what was the time required for the room to reach a stable temperature?
MR CFD Support –
Thank you for your kind words! In the simulation, the time required for the room to reach a stable temperature would depend on various factors including the initial room temperature, the specifications of the room materials, and the settings of the heat source—the radiator. During CFD analysis, such information would typically come from observing the temperature profiles or contours over simulation time. Unfortunately, specific information regarding the stabilization time isn’t provided in the initial review request, but you can typically find such details in the study’s results section or summary of findings based on transient heat transfer analysis in ANSYS Fluent.
Estefania Kessler –
Can the simulation handle different radiator shapes?
MR CFD Support –
Yes, you can adjust the parameters to match the shape of your specific radiator.
Haleigh Kutch –
The methodology here is informative, but I’m curious—what specific indicators or outputs does this simulation measure to assess heat distribution within the room?
MR CFD Support –
The main outputs to assess heat distribution within the room include temperature contours, which illustrate temperature variance across the room over time, and velocity vectors or flow patterns to visualize heated air movement. Additionally, the simulation may measure the heat transfer rate from the radiator and natural convection current development due to buoyancy effects.
Prof. Buddy Schowalter –
I just want to express my appreciation for the way this material is presented. It’s detailed and precise, providing a clear understanding of the simulation process and the methodology applied. Well done!
MR CFD Support –
Thank you so much for your kind words! We’re thrilled that you found the material comprehensive and clear. Your feedback is appreciated, and it inspires us to keep delivering quality learning materials.
Prof. Vern Wintheiser –
The simulation mentions using transient analysis. Could you explain why transient analysis is essential for this radiator problem?
MR CFD Support –
The transient analysis is essential in this radiator problem because it allows us to observe how the heat transfer changes and evolves over time within the room. This is crucial for assessing the radiator’s performance in real-world conditions where the room temperature changes dynamically, especially when the radiator turns on or off or when exterior temperatures fluctuate.
Dr. Eugenia Howell MD –
I just want to say thank you for providing such a comprehensive kit to understand transient heat transfer using ANSYS Fluent. The step-by-step guide on the radiator simulation was incredibly useful, and seeing the buoyancy effect in action really cemented my understanding of natural convection in room heating. Great job on the design and simulation detail!
MR CFD Support –
Thank you so much for your kind words! We’re thrilled to hear that the Radiator Transient Heat Transfer in a Room Simulation was helpful to your learning experience. Your feedback is greatly appreciated and motivates us to continue providing high-quality CFD training materials. If you have any further questions or need additional resources in the future, please don’t hesitate to reach out to us.
Jerrell Harris –
This training clearly outlined the transient behavior of heat transfer from the radiator. I could visually track temperature changes over time within the simulated room space. Well-structured and informative!
MR CFD Support –
Thank you for your kind words! We’re thrilled to hear that our Radiator Transient Heat Transfer in a Room Simulation training provided you with clear and visual insights into heat distribution dynamics. Your feedback is very much appreciated!
Manuel Reichel –
I cant find this geometry file in grab-cad website, can you please provide me another link to download this model…
MR CFD Support –
Hello, we are very glad that you visited our site.
Please go to the following address:
http://www.mr-cfd.com/shop/radiator-heat-transfer-inside-a-room-transient-cfd-simulation
Dr. Triston Herzog –
I’m blown away by how comprehensive the simulation seems. Could you elaborate on how the buoyancy effect was factored into the simulation and its impact on the heat distribution within the room?
MR CFD Support –
In the simulation, the buoyancy effect was factored in by activating the gravity settings within the ANSYS Fluent software, ensuring that the natural convection current could be appropriately simulated. This had a significant impact on the heat distribution as it allowed the simulation to capture how warm air from the radiator rises and cooler air descends, which is crucial for an accurate representation of the heat transfer within the room. Thank you for your positive feedback on the thoroughness of the simulation. We aim to provide a detailed and realistic simulation environment in all our projects.
Camden Muller V –
I’m impressed with the level of detail in the simulation setup! Could the provided training help me predict seasonal variations in room heating requirements?
MR CFD Support –
Thank you for your positive feedback! The provided training focuses on the principles of transient heat transfer and convection, which are fundamental to understanding room heating requirements. While it doesn’t specifically cover seasonal variations, the concepts learned can be applied to model different scenarios, including seasonal changes, by adjusting the ambient temperature and heat transfer coefficients accordingly.
Samanta Mante –
In terms of setting up the simulation, can you elaborate on how unsteady state conditions were handled, particularly with regards to temperature monitoring over time?
MR CFD Support –
In the simulation of transient heat transfer by the radiator in a room, time-dependent conditions were managed using a transient solver. This allows for the calculation of temperature changes over time within the room. Temperature monitoring was set up at specific locations to track the changes at various time steps throughout the simulation, ensuring a thorough understanding of how the heat from the radiator dissipates into the room air over time.
Miracle Larkin –
I found your training incredibly informative! It helped me understand transient heat transfer much better. Do the aluminum fins increase the heat transfer significantly in the simulation compared to a model without them?
MR CFD Support –
Thank you for your positive feedback! Yes, the aluminum fins play a crucial role in enhancing heat transfer. Their high thermal conductivity allows efficient thermal energy distribution from the hot water pipes to the ambient air in the room, thus accelerating the heat transfer process by increasing the surface area for convection.
Mr. Izaiah Crist –
I’m pleased with the level of detail the simulation provides about heat transfer within a room. It’s great to see how the radiator affects the room temperature over time.
MR CFD Support –
Thank you for your kind words! We’re glad that the radiator heat transfer simulation met your expectations and provided you with valuable insights. If you have any further questions about the simulation or other products, please don’t hesitate to reach out.