NACA 0012 Airfoil, Compressible Flow CFD Simulation
$100.00 Student Discount
- The problem numerically simulates NACA 0012 Airfoil (Compressible Flow) using ANSYS Fluent software.
- We design the 2-D model by the Design Modeler software.
- We Mesh the model by ANSYS Meshing.
- The model mesh is structured, and 35000 cells have been created.
- We apply a Density-based solver to define the compressible flow.
- We determine the Mach number for the inlet boundary condition.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
NACA 0012 Airfoil (Compressible Flow) CFD Simulation, ANSYS Fluent Tutorial
This simulation is about NACA 0012 airfoil via ANSYS Fluent software. We perform this CFD project and investigate it by CFD analysis.
In general, the airfoil is the same as the plane’s wing cross-section, wind turbine blade, helicopter, and so on. However, it should be noted that different airfoils can be used to construct an aircraft wing, and the choice of airfoil type in different applications depends on the aerodynamic characteristics.
Geometric defining parameters include chord line, angle of attack, leading edge, and trailing edge. The direction of the airflow into the airfoil is defined by the angle of attack (the angle between the chord and the horizontal direction of the airflow velocity).
In the present case, the attack angle is 5 degrees; thus, the horizontal component of the airflow direction is defined as 0.996 (cos5), and the vertical component is equal to 0.087 (sin5).
This project aims to investigate the airflow behavior and the pressure distribution around the airfoil and study the drag and lift forces.
We design the geometry of the present model by Design Modeler software. We mesh the model with ANSYS Meshing software. The model mesh is structured, and 35000 cells have been created.
Airfoil Methodology
In this simulation, the density-based solver is performed because the airflow is considered compressible.
Defining the Mach number in the boundary conditions is necessary for compressible flows. The Mach number is equal to the ratio of the speed of an object in a fluid to the sound speed in the same fluid in which that object moves.
For example, the sound speed in the air with a temperature of 25 degrees Celsius is 343 meters per second.
In general, the simulation of an airfoil requires the definition of a far-field boundary condition, and therefore the Mach number for the flow field must be defined, the value of which in the present case is 0.6.
Airfoil Conclusion
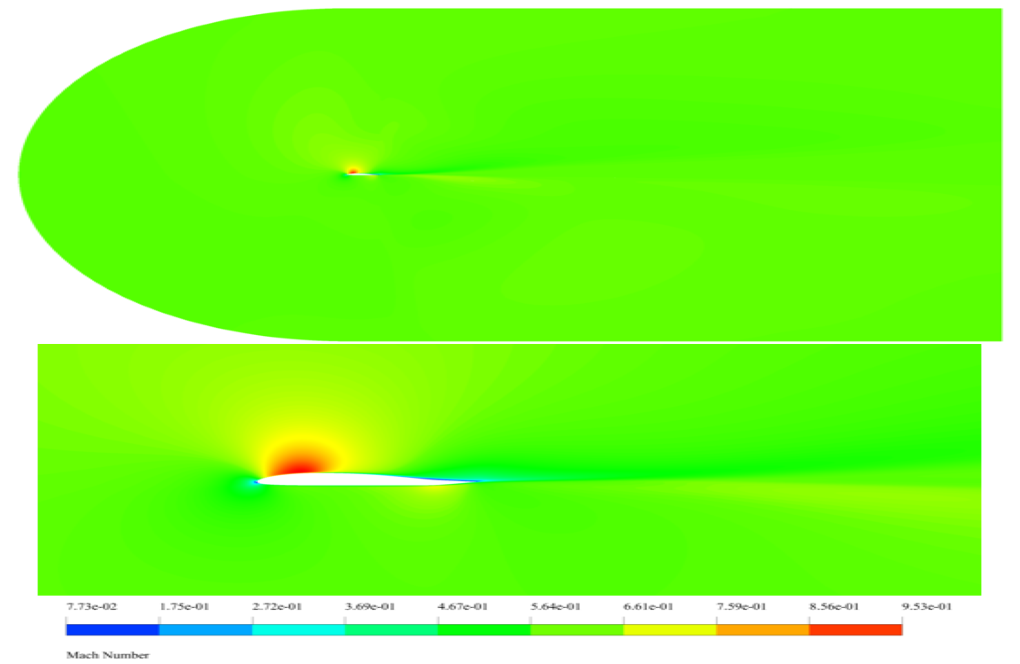
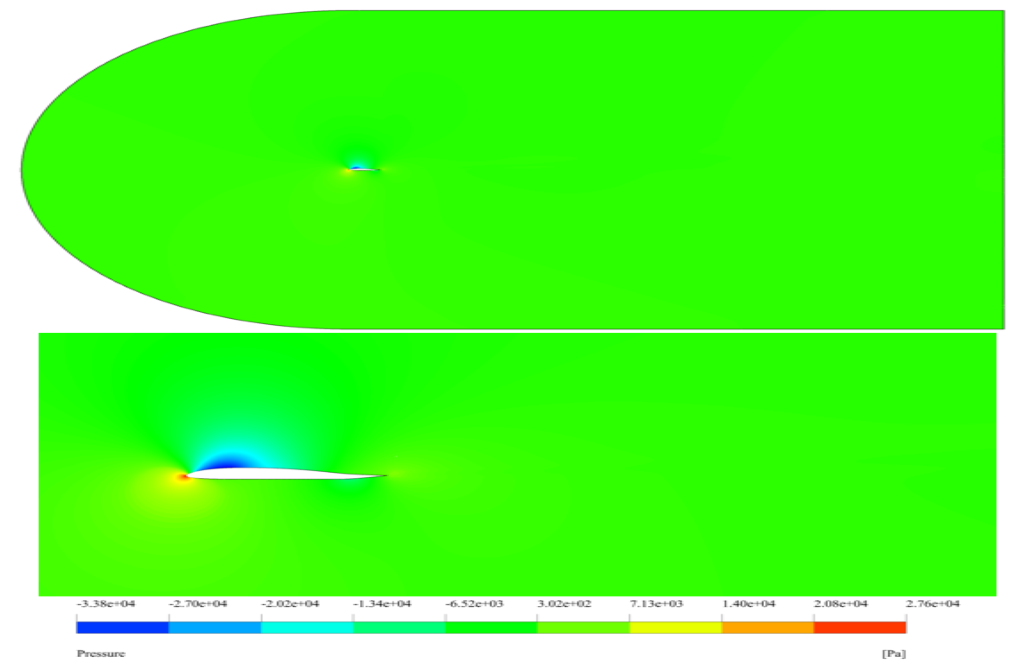
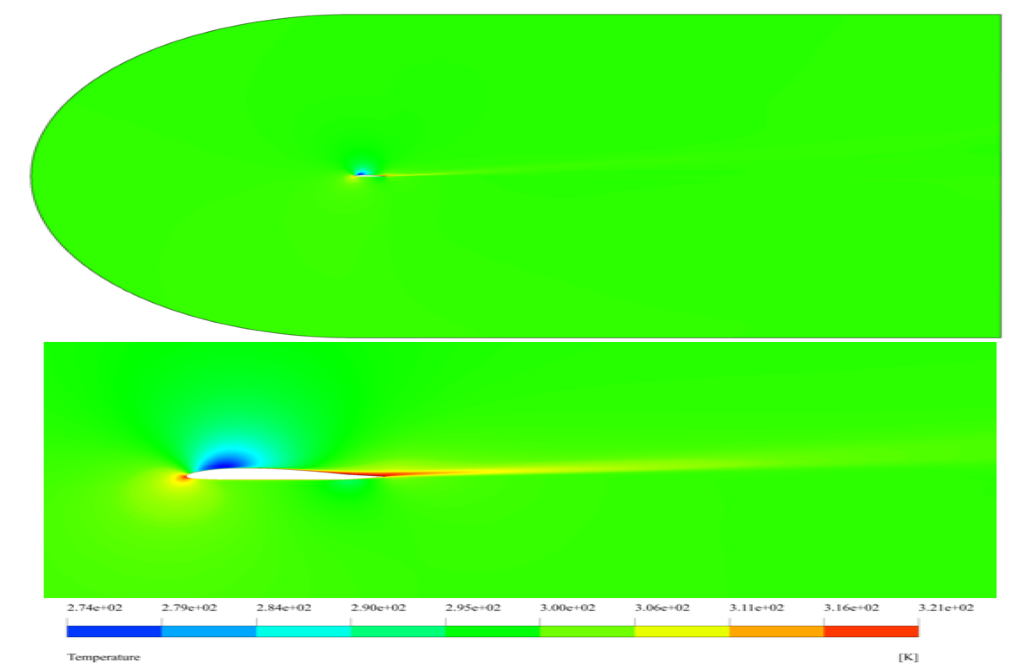
After simulation, we obtain two-dimensional contours of pressure, velocity, temperature, density, and Mach number, as well as two-dimensional streamlines.
The results show that at the leading edge of the airfoil, the highest pressure appears, caused by the airflow’s direct contact with the airfoil’s leading edge.
The structure of the airfoil is such that the airflow on its upper surface faces the greatest pressure drop. This pressure difference between the top and bottom of the airfoil body causes the upward movement of the wing.
Also, the velocity changes are in perfect accordance with the pressure distribution. Where there is the greatest pressure, the least velocity appears, and vice versa.




Rasheed Larson –
Can this simulation be customized to model the airflow around different types of airfoils?
MR CFD Support –
Yes, we can accommodate your desired simulations. Please share more details about your specific requirements.
Ms. Litzy Osinski –
Well done!
Pinkie Armstrong –
The tutorial was detailed and very helpful. I managed to simulate my airfoil, and the pressure distribution was exactly as expected! Liftdrag forces were also within expected ranges.
MR CFD Support –
Thank you for your positive feedback! We’re delighted to hear that our tutorial was helpful for you and met your expectations for simulating the NACA 0012 airfoil. Your success with accurately predicting pressure distribution and lift/drag forces is precisely what we aim for with our learning products. If you have any more questions or need further assistance in the future, remember that we are here to help. Keep soaring in your CFD analysis ventures!
Chance Gibson –
Fantastic learning tool for understanding compressible flow over an airfoil! The results gave great insight into how the pressure and velocity vary around the NACA 0012 and its effects on lift and drag. It’s very effective for visualising the impact of different angles of attack and Mach numbers in aerospace applications.
MR CFD Support –
Thank you for your positive feedback! We’re thrilled to hear that our simulation tool for the NACA 0012 airfoil has provided valuable insights into compressible flow dynamics and has enhanced your understanding of aerodynamic principles. We appreciate you taking the time to share your experience and we’re glad to support your learning journey!
Miss Nova Turner –
The results for this NACA 0012 airfoil simulation sound thorough. The use of a structured mesh with 35,000 cells surely helped in capturing the precise aerodynamic features. The simulation parameters, including the angle of attack and Mach number settings, seem meticulously chosen to reflect realistic flying conditions. Comprehending how the pressure distribution affects the lift is fascinating, and the density-based solver must have provided accurate compressibility effects. Furthermore, the detail on the pressure-induced velocity changes reaffirms confidence in the quality of these CFD findings.
MR CFD Support –
Thank you for your thoughtful review! We are thrilled to hear that the intricacies of the mesh, the chosen simulation parameters, and the aerodynamic analysis methodology in our NACA 0012 airfoil tutorial provided you with a comprehensive understanding of the subject matter. It is rewarding to know that our focus on accurate replicability and detail aligns with your appreciation for diligent simulations. Should you have further interest in our simulations or require additional insight, please don’t hesitate to ask!
Stone Christiansen –
I just completed working through the NACA 0012 Airfoil simulation tutorial and the explanations provided for each step were extremely clear. I particularly appreciated the way the results section detailed the relationship between pressure distribution and velocity changes, and how this leads to lift.
MR CFD Support –
Thank you for your positive feedback! We are thrilled to hear that you found the tutorial clear and informative. It’s great that the results section gave you deeper insight into the aerodynamic principles at work. If you have any further questions or need assistance with another simulation, feel free to reach out. We’re here to help!
Demond Mertz –
How accurate is this simulation?
MR CFD Support –
The simulation is based on well-established physical principles and mathematical models, and we validate our results against experimental data to ensure accuracy.
Jan Feeney –
NACA 0012 Airfoil CFD simulation explained how the drag and lift forces on the airfoil were studied. Could you please tell me how accurate the results of the simulation were compared to physical wind tunnel tests?
MR CFD Support –
Regarding the accuracy of the results from our NACA 0012 Airfoil CFD simulation compared to wind tunnel tests, the simulation framework in ANSYS Fluent is designed to replicate physical phenomena with high fidelity. By accurately defining the airfoil geometry, boundary conditions, and physical properties of the flow, we strive to ensure that our CFD results closely match experimental data. Although some differences between simulation and real-world testing can occur due to simplifications and model assumptions, we calibrate our models based on benchmarks and available literature to provide results that are as accurate as possible within the constraints of computational resources.
Cyril Fadel –
I have completed the NACA 0012 Airfoil simulation and learned so much about aerodynamics. The results were impressive, especially understanding how pressure distribution affects lift. Can’t wait to apply this knowledge!
MR CFD Support –
Thank you for your positive feedback! We’re thrilled to hear that you found the simulation informative and that you’re eager to apply what you’ve learned about aerodynamics and pressure distribution. Your enthusiasm for CFD learning is exactly what we strive for at MR CFD. Looking forward to offering you more valuable experiences!