Rotation of a Cube Considering Sloshing Simulation, ANSYS Fluent Training
$160.00 Student Discount
- The problem numerically simulates the Rotation of a Cube Considering Sloshing using ANSYS Fluent software.
- We design the 3-D model with the Design Modeler software.
- We mesh the model with ANSYS Meshing software, and the element number equals 168367.
- We perform this simulation as unsteady (Transient).
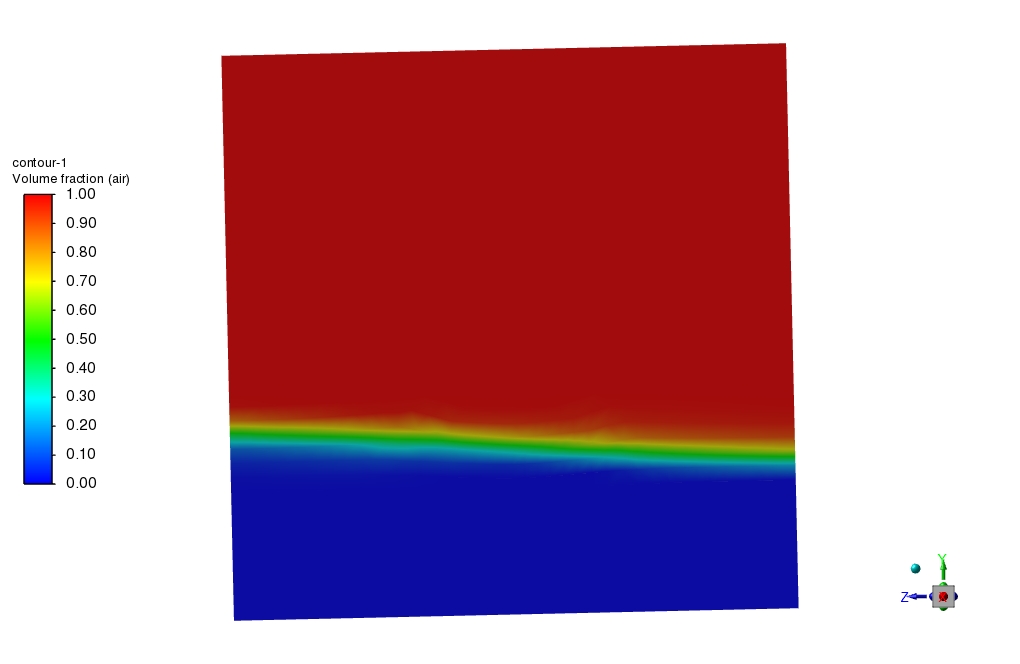
- We use the VOF Multiphase model to define water and air.
- We use a UDF to define the variable angular velocity of the cube’s rotation.
Click on Add To Cart and obtain the Geometry file, Mesh file, and a Comprehensive ANSYS Fluent Training Video.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Description
In this project, the rotation of a cube containing water and air is investigated by ANSYS Fluent software. The cube rotates around the Y-axis with variable angular velocity. The cube’s distance to the rotation axis is equal to 1 m.
The angular velocity of rotation varies with time as the function 0.252273*sin(2.53*time+36800).
The fluid domain geometry is designed in the Design Modeler, and the computational grid is generated using Ansys Meshing. The mesh type is unstructured, and the element number is 168367.
Cube Methodology
The interaction of water and air inside the cube is modeled using the Volume of Fluid (VOF) multiphase approach. VOF multiphase approach is considered since it is an efficient and precise approach for capturing the interface location between phases.
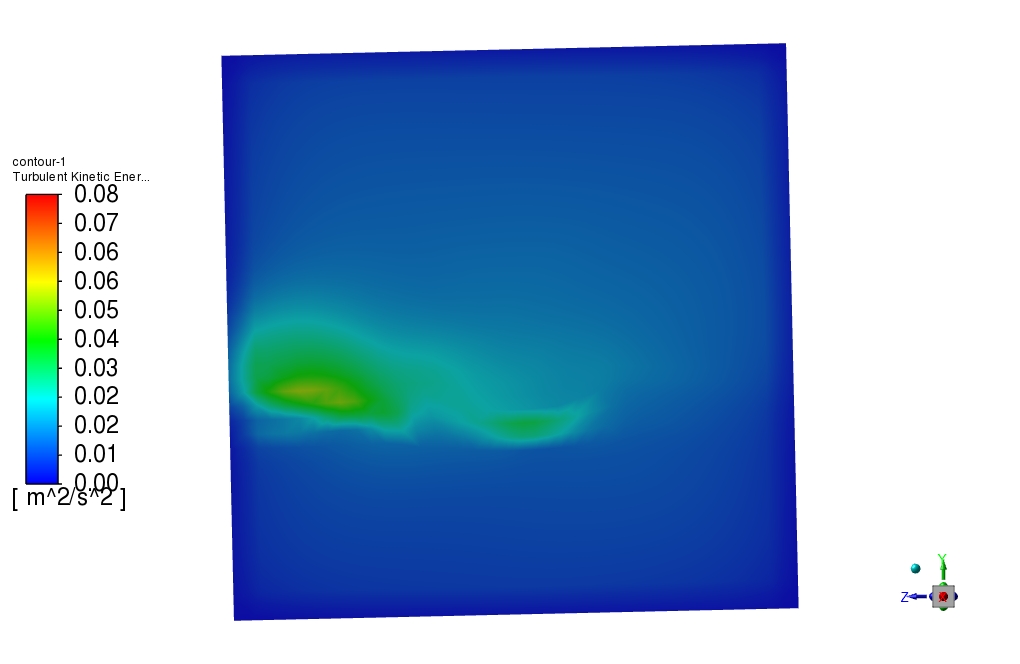
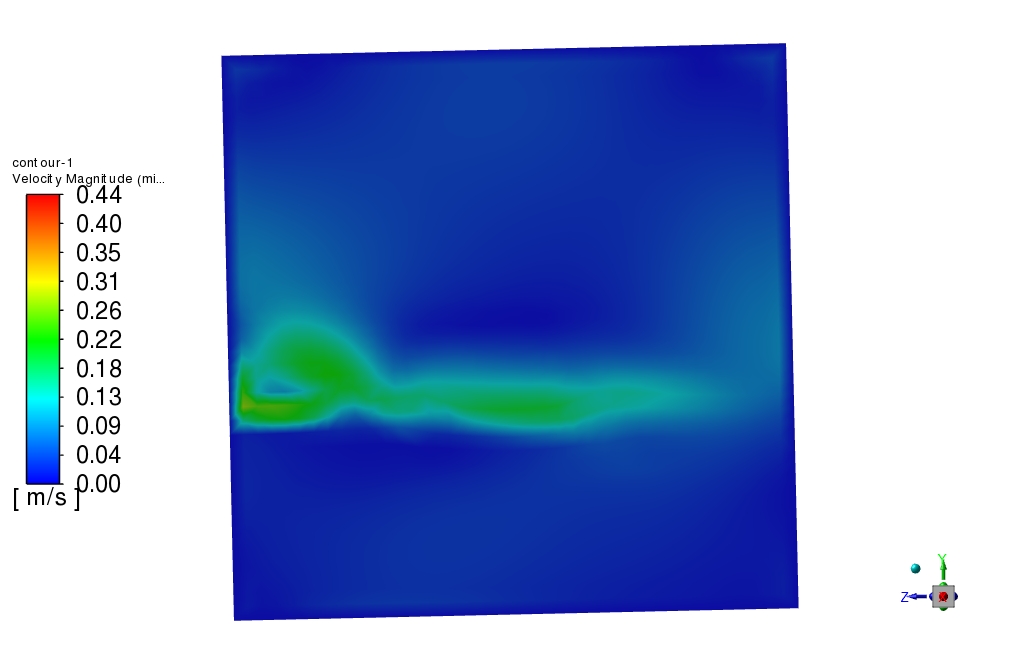
A User Defined Function (UDF) defines the variable angular velocity of the cube’s rotation. Also, the solver is Transient.
Cube Conclusion
This project investigates the simplified sloshing effect in fluid containers where a situation similar to the one studied here can occur due to the acceleration of the carrier vehicle.
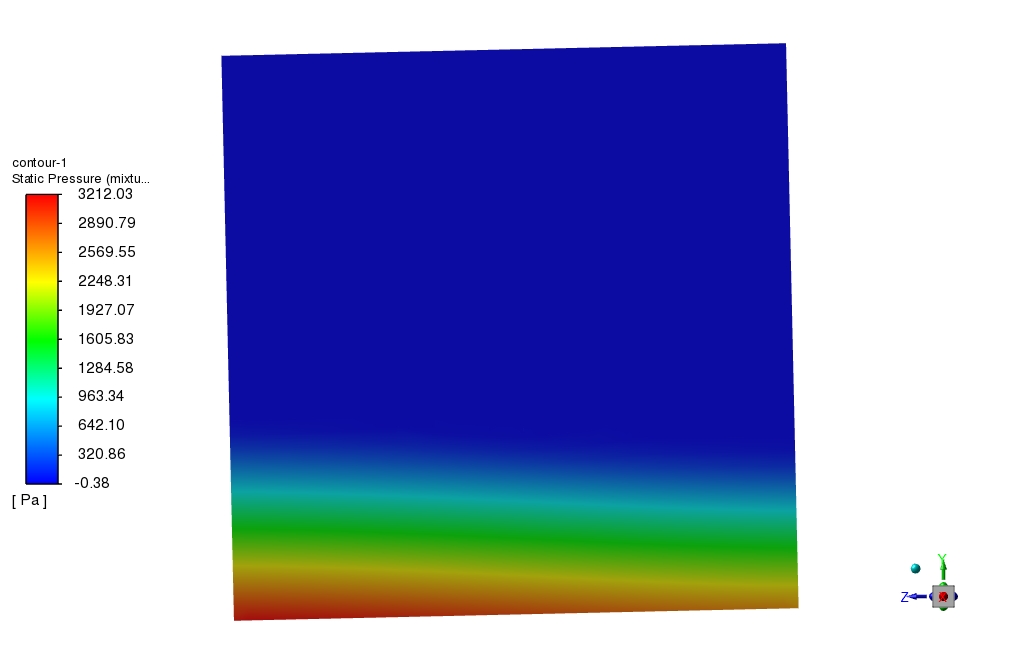
Results show that pressure on the bottom surface of the cube varies with radial distance to the OO line. Pressure increases as the position are away from the OO’s line.





Zelda Sauer –
How does the simulation handle the interaction between the water and air in the cube?
MR CFD Support –
The simulation uses a Volume of Fluid (VOF) model to handle the multiphase interaction between the water and air. This model can accurately capture the interface between the two phases.
Fern Donnelly –
I’m thrilled with how immersive the Rotation of a Cube simulation training is! The use of VOF for capturing fluid interaction is really fascinating.
MR CFD Support –
Thank you for your positive feedback! It’s great to hear that you found the training both immersive and educational. We continuously strive to provide high-quality, realistic simulations to enhance learning experiences. If you have any questions or need further assistance, don’t hesitate to reach out!
Vladimir Eichmann –
The tutorial eagerly explained every detail and made simulating sloshing in a rotating cube crystal clear—the VOF model’s efficacy in distinguishing air and water notable. The provided UDF took the intimidation out of applying complex boundary conditions. Stellar work by the team!
MR CFD Support –
Thank you for your glowing review! We are thrilled to hear that the tutorial was comprehensive and instrumental in clarifying the complex concepts of sloshing simulation and that you found the use of VOF and UDF helpful. Your feedback is greatly appreciated, and it motivates us to continue delivering high-quality learning materials.
Maudie Hauck –
Everything I learned on sloshing kinetics from this training has been super helpful for my studies. The approach was very effective and practical for visualizing the fluid behavior in a rotating cube. Fantastic learning resource!
MR CFD Support –
We’re delighted to hear how beneficial the training on sloshing kinetics proved for you! It’s great when our resources can contribute to your studies and understanding of fluid behaviors. Thank you for your positive feedback!
Ally Lang –
Beautiful implementation of the sloshing simulation in a rotating cube context! The use of a sine function for angular velocity showcases the dynamic response quite impressively.
MR CFD Support –
Thank you for your kind words! We’re glad to hear that you appreciate the complexity of the rotating cube simulation and the accuracy brought about by the UDF. It’s great to know our efforts to create realistic and dynamic models resonate with our users.
Lulu Kshlerin –
The project’s explanation of results is captivating and fills niceties. Great job in detailing how sloshing dynamics within a rotating cube affects pressure distribution. Such insights could be pivotal for understanding fluid behavior in moving vessels or rotating machinery.
MR CFD Support –
Thank you for your positive feedback! We are thrilled to hear you found the results and insights provided in our CFD simulation on cube rotation and sloshing dynamics valuable. Understanding fluid behavior in dynamic conditions is indeed key for various applications, and we are glad our project could provide such an understanding. If you have further inquiries or need additional information, feel free to reach out!
Antonina Keeling V –
How is the rotation of the cube modeled in this simulation?
MR CFD Support –
The rotation of the cube is modeled using a dynamic mesh with a user-defined function (UDF) that specifies the rotational motion. This allows for a realistic representation of the cube’s rotation.
Kenny Klocko II –
How is the turbulent flow in the cube modeled?
MR CFD Support –
The turbulent flow in the cube is modeled using a turbulence model, such as the k-epsilon or k-omega model. This can accurately capture the complex flow patterns inside the rotating cube.
Myrtle Hyatt –
The product quality and detailed explanation in the ‘Rotation of a Cube Considering Sloshing Simulation’ were outstanding. I especially appreciated the clear outline of how angular velocity impacts pressure distribution within the cube.
MR CFD Support –
Thank you for your wonderful feedback! We’re delighted to hear that you found the training so informative and clear, especially regarding the relationship between angular velocity and pressure distribution. Your satisfaction with the quality of our product is our top priority. We aim to continue providing detailed and insightful simulations. Thank you for choosing our services!
Mrs. Alana Jenkins –
The results you’ve reported are fascinating! It really shows the complexities of sloshing effects captured through simulation. Did the training cover the analysis of how these pressure variations can impact the structural integrity of the cube or on the forces experienced on its walls?
MR CFD Support –
We are thrilled to hear you valued the insights from our training! The primary focus of the training session revolves around sloshing dynamics within a rotating cube and its impact on internal pressure distribution. While the fundamental training emphasizes fluid behaviors and pressures, a comprehensive engineering analysis may entail additional considerations of the forces and their implications on the structure, which can be advanced topics for additional study or later modules.
Dr. Shad Ortiz –
The training makes the concept of sloshing quite clear. Particularly impressed with the application of the UDF for variable angular velocity!
MR CFD Support –
We’re glad to hear that you’re impressed with the training and found the UDF application for variable angular velocity helpful. It’s great to know that the concepts are clearly conveyed through our training. Thank you for your positive feedback!
Alexandrea Bradtke –
The results mention pressure changes in relation to the distance from the OO line. Does this mean that pressure distribution changes uniformly across the cube’s bottom or there are specific patterns formed due to the rotation?
MR CFD Support –
The pressure distribution on the bottom of the cube does not change uniformly due to the rotation. Due to the centrifugal forces in action, pressure is expected to be higher at points further away from the axis of rotation (OO line). Specific patterns can form as a result of the sloshing dynamics, which depend on the interaction between the rotating motion and the fluid’s response to it.
Sasha Kerluke II –
I was impressed with the dynamic rotation simulation and how the UDF captured the variable angular velocity. Excellent work!
MR CFD Support –
Thank you for your kind words! We’re thrilled to hear you appreciated the use of a User Defined Function (UDF) to accurately simulate the variable angular velocity in the sloshing simulation project. If you have any further questions or need assistance on similar projects, feel free to reach out to us.
Lamont White DDS –
I was really captivated by the results displayed for the different pressures depending on the radial distance from the rotation axis! This training helped me understand sloshing dynamics within rotating objects far better.
MR CFD Support –
We are pleased to hear that the training has deepened your understanding of sloshing dynamics! Thank you for taking the time to share your positive experience with the Rotation of a Cube Considering Sloshing Simulation training material. Your encouragement motivates us to keep providing high-quality learning resources.
Natalie Kirlin –
Fantastic simulation study! The details about the varying angular velocity and VOF multiphase model usage were key highlights for me.
MR CFD Support –
We are really glad to hear that you appreciated the work involved in the simulation study and its technical details. Your feedback encourages us to continue delivering high-quality training and simulation services. Thank you!
Mohammed Cassin –
What an incredibly descriptive and educational presentation of sloshing dynamics in a rotating cube! The methodology’s attention to detail, using the VOF approach and UDF for variable angular velocity, facilitates a comprehensive understanding of fluid behavior under rotational forces.
MR CFD Support –
Thank you so much for your positive feedback. We’re thrilled to hear you found the sloshing simulation within a rotating cube both informative and instructional. It’s great to see our attention to detail and methodology appreciated!
Bill Morissette –
Very pleased with how the cube rotation simulation considering sloshing turned out. The complexity of multi-phase interactions in dynamic conditions was well-illustrated.
MR CFD Support –
Thank you for your kind words! We’re thrilled to hear you found the cube rotation and sloshing simulation insightful and representative of the multiphase dynamics. It’s always our goal to deliver complex concepts in an understandable and accurate way. If you have any more feedback or need further insight, feel free to reach out!
Ansley Abernathy PhD –
The project looks intriguing! Was the transient solver setup challenging given the variable angular velocity, and did you face any convergence issues during the simulation?
MR CFD Support –
Thank you for the kind words about our project! Setting up the transient solver with the variable angular velocity, defined by a User Defined Function (UDF), was indeed a meticulous task, but it was essential for accurately simulating the cube’s dynamics. While transient simulations can pose convergence challenges, particularly when dealing with moving boundaries and multiphase flows such as sloshing, careful setup and tuning of the solver parameters helped in achieving stability and convergence of the results.
Deborah Armstrong –
Is the variable angular velocity implemented in the model critical for accurately simulating the sloshing phenomenon?
MR CFD Support –
Yes, the variable angular velocity is crucial for simulating the sloshing phenomenon as it recreates the dynamic environment that is usually responsible for sloshing in real systems. By utilising a UDF to replicate this varying motion, simulations can mimic the actual conditions leading to sloshing, providing insights into how fluid behavior changes over time with changing velocities.
Herbert O’Reilly –
Are there any visual aids provided like animations or graphs, so I can better understand the sloshing effect inside the cube throughout the simulation?
MR CFD Support –
Animations and graphical representations are valuable tools to visualize and understand the sloshing effect in a rotating cube simulation. These can help better grasp how the liquid motion within the cube responds to changes in angular velocity over time.
Dr. Stephen Hyatt –
The dynamically varying angular velocity seems complex. Does the provided User Defined Function (UDF) account for appropriate changes during the simulation?
MR CFD Support –
Yes, the User Defined Function (UDF) is specifically scripted to manage the time-dependent angular velocity that changes as a sine function of time, ensuring that the variable angular velocity is accurately represented throughout the transient simulation.