Spray CFD Simulation using Injection in DPM
$100.00 Student Discount
- The problem numerically simulates the process of water spray into a cubic space using ANSYS Fluent software.
- We design the 3-D model with the Design Modeler software.
- We mesh the model with ANSYS Meshing software, and the element number equals 25464.
- We perform this simulation as unsteady (Transient).
- We use the Discrete Phase Model (DPM) model to define a spray process.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Spray CFD Simulation using Injection in DPM, ANSYS Fluent Training
The present problem studies Spray CFD Simulation using Injection in a Discrete Phase Model (the process of water spray into a cubic space) by ANSYS Fluent software. Spray CFD Simulation using Injection in Discrete Phase Model.
The present study aims to investigate water flow behavior during the spraying process from a tiny circular section to the inner space of a zone with a larger volume, which examines the behavior of water flow by tracing every particle. The simulation is time-dependent, and the solver is unsteady.
The geometry of this model consists of a rectangular cube zone with a circular cross-section as the input of the fluid flow on the upper wall of the domain. This geometry is drawn by Design Modeler software.
The model is then meshed by ANSYS Meshing software. The model mesh is unstructured, and 25,464 cells have been created.
Spray Methodology
Because particles must move discretely in a continuous medium, the Lagrangian perspective should be used to simulate this model. Therefore, a discrete phase model (DPM) is used in this modeling.
This approach means they must be tracked particle by particle in a continuous environment to analyze their behavior. So when using the DPM, an injection must be defined for the particles.
The material of the injected particles in the present model is water, and it enters the space from the inlet boundary of the model. The injection process is in the form of a surface, and the type of water particles is inert.
Spray Conclusion
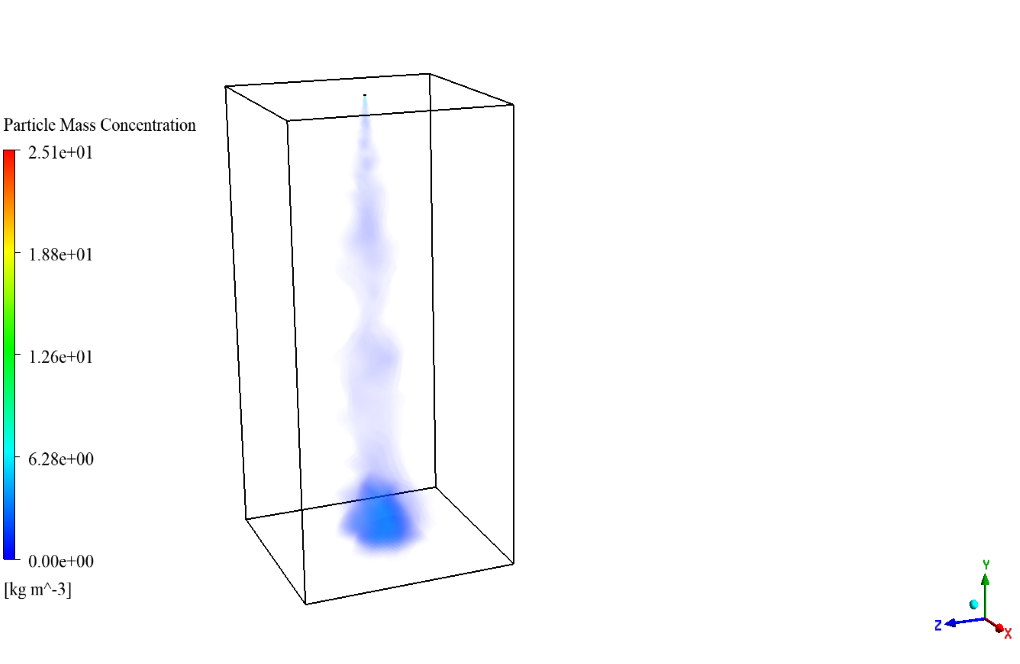
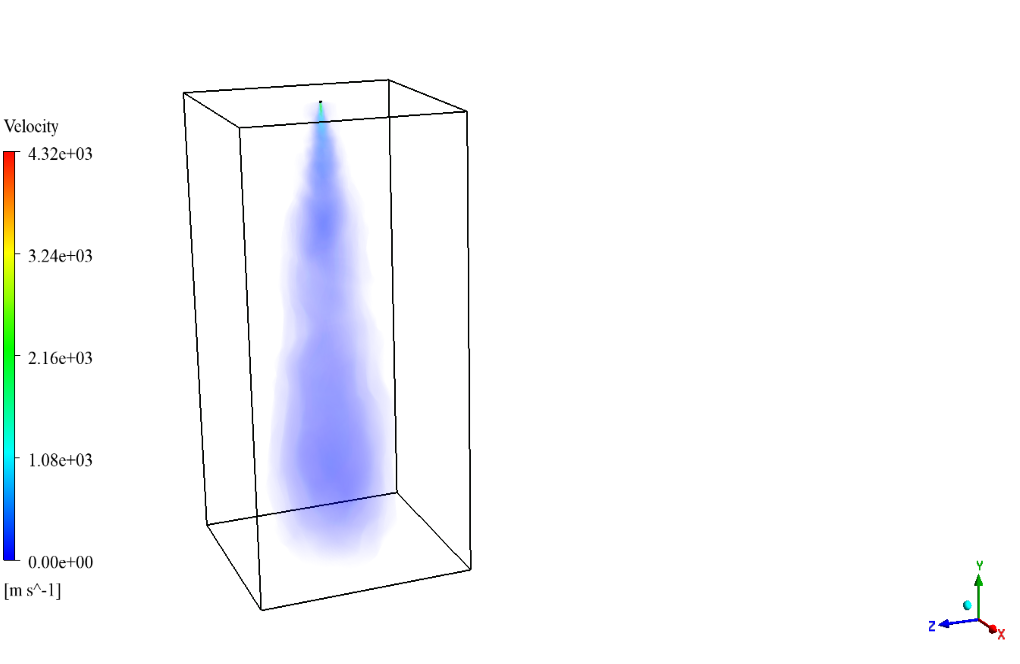
After simulation, the 2D and 3D contours related to the velocity and mass concentration of the water particles are obtained in the last second of the simulation process.
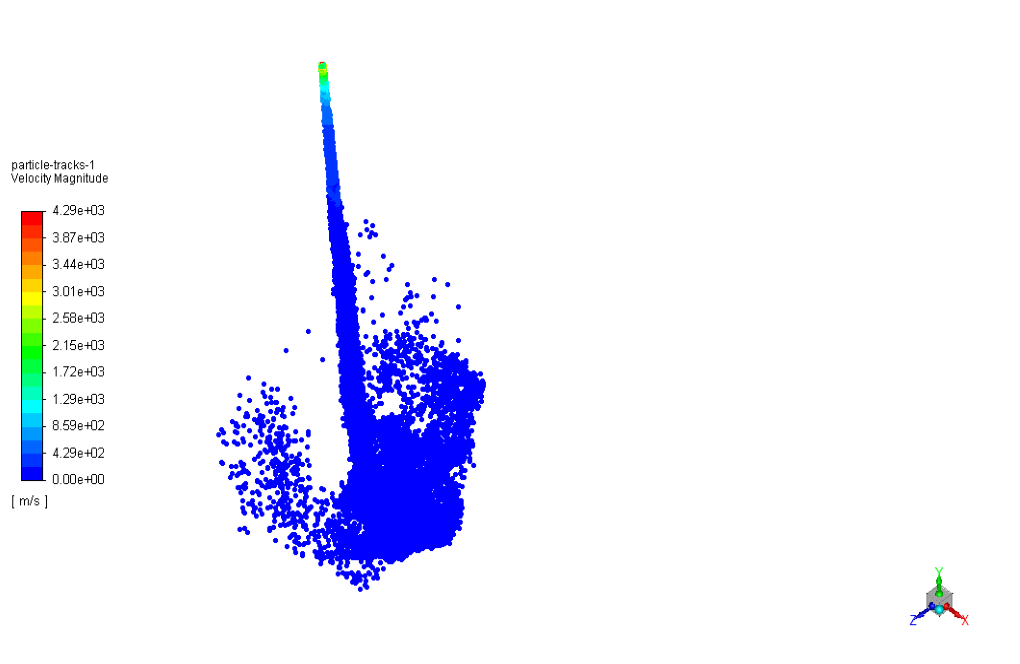
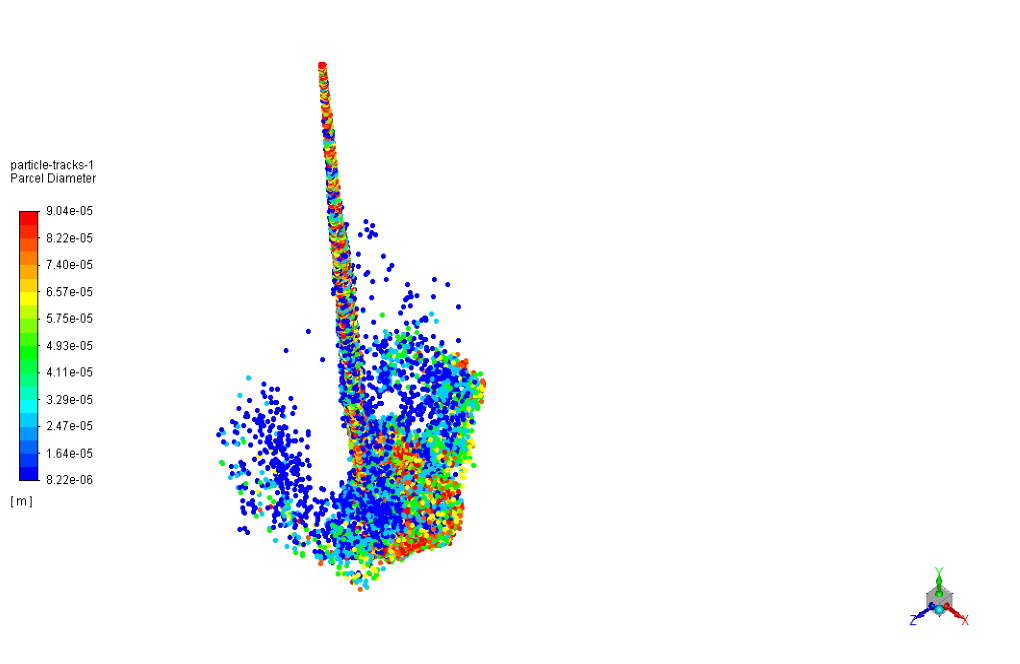
Also, particle track related to spraying particles in 3D space is obtained based on the speed of spraying particles and the diameter of spraying particles.
The figures show that the injection of water particles is done correctly. These water particles are dispersed discretely from the upper inlet of the cube to the inside of the model and are distributed inside the model.





Kyra Wisozk IV –
How does the simulation model the spray injection?
MR CFD Support –
The simulation uses the Discrete Phase Model (DPM) in ANSYS Fluent to model the spray injection. The DPM is used to track the trajectory of the discrete phase particles or droplets.
Margaretta Sporer –
The explanation of the product is very detailed and technically informative. I believe that this guide would be incredibly helpful for grasping the intricacies of performing a Spray CFD simulation using DPM in ANSYS Fluent.
MR CFD Support –
Thank you very much for your kind words and positive review! We are thrilled to hear that our Spray CFD Simulation guide met your expectations and provided the detailed information you needed. If you need any further assistance or have more questions in the future, please feel free to reach out to us. We are always here to support your learning journey with our products!
Mrs. Magnolia Vandervort Sr. –
I found the descriptions of the DPM and how particles are tracked fascinating. Could you please clarify how the injection rate and particle size were determined in this simulation?
MR CFD Support –
In this simulation, the injection rate and particle size for the DPM are typically determined based on the specific requirements of the study, such as the characteristics of the physical spray system being modeled or experimental data. The values are inputted as parameters within ANSYS Fluent’s injection settings, tailored to accurately represent the behavior of the water spray in the virtual environment.
Ransom Johns –
Hi, I wanted to make this product, and I had a question? Is the project’s unsteady resolved?
MR CFD Support –
Yes, this project is solved by applying a Transient solver. So, you can capture unsteady particle tracking.
Dr. Milton Morissette DDS –
I appreciate the detailed explanation of the simulation project. The use of DPM to model spray behavior seems extremely practical and useful. I am curious to know how well this model might scale for much larger or more complex spraying applications.
MR CFD Support –
Thank you for your positive feedback on our Spray CFD Simulation tutorial. While the simulation in this training was performed on a specific scale within a cubic space, the principles applied here using Discrete Phase Model (DPM) and particle injection techniques can indeed be scaled up for larger or more complex spraying applications. As the complexities and scale change, additional considerations such as increased computational resources, refined meshing strategies, and more computational time for accurately tracking a large number of particles might be necessary. However, the fundamental mechanisms of particle injection and behavior analysis remain applicable. If you plan to work on a larger scale project and need further assistance or if you have any specific requirements in mind, please let us know, and we will be glad to discuss potential approaches and solutions.
Jeramie Zboncak –
The overview was wonderful! The way the DPM is used to track the water particles seems meticulous. Thanks for such a detailed explanation in your study.
MR CFD Support –
Thank you for your positive feedback! We are glad to hear you found our explanation detailed and helpful. If you have any more questions or need further assistance, feel free to reach out. Your satisfaction is our top priority!
Mr. Pedro Fadel –
The training on spray CFD simulation was fantastic! I really appreciated the clear explanation of all steps and settings. The visualization of particle tracks and the behavior analysis of water flow are amazing. Could see how this would benefit numerous engineering applications.
MR CFD Support –
Thank you for your positive feedback on our Spray CFD Simulation using Injection in DPM training. We are thrilled to hear that the content was clear and the visualizations met your expectations. It’s great to know that our tutorial can contribute to various engineering projects. Your satisfaction is our top priority!
Shania Bashirian –
The MR-CFD is described efficiently.
Mr. Loy Pacocha II –
This simulation is a fantastic tool for understanding complex flow dynamics!
Heloise Connelly V –
I found the 3D contours quite insightful. Great job visualizing the particle dispersal!
MR CFD Support –
We’re delighted to know that our 3D contours enhanced your understanding of the particle dispersal. Thank you for acknowledging the effectiveness of our visualization!
Deshawn Prohaska I –
I’m truly amazed by how realistically the spray simulation mimicked the actual spray dispersion. Was waviness or any perturbations in the particle path taken into account to emulate real-world behaviors of sprays?
MR CFD Support –
Thank you so much for your kind words! Regarding your question, in such simulations, certain complexities like waviness and perturbations can indeed be modeled to enhance realism. Perturbations can be introduced to replicate instabilities in the particle paths, thereby emulating real-world spray behavior. These phenomena are typically accounted for within the discrete phase modeling by adjusting initial conditions and interaction parameters to reflect real-world conditions accurately.
Mrs. Roxanne Casper Sr. –
What type of injection is applied for the water particles in the DPM simulation? And how does it affect the resulting spray behavior inside the cubic space?
MR CFD Support –
The type of injection applied for water particles in the DPM simulation is a surface injection, where the particles are treated as inert. This setup allows for an accurate representation of the spray behavior as it replicates the discrete dispersion of water particles from the upper inlet, reflecting how they would move and spread within the cubic space.
Kamryn Emard Jr. –
The ANSYS Fluent Training for the Spray CFD Simulation using Injection in DPM seems comprehensive. I found the simulation approach using the Lagrangian perspective to track individual particles quite fascinating. This more detailed modeling can be critical for certain engineering applications such as fuel injector designs.
MR CFD Support –
We’re glad to hear that you appreciate the comprehensive nature and depth of the training. The use of a Lagrangian perspective is indeed key to accurately modeling particle behavior in a flow, and it’s great to see you recognize its importance in applications like fuel injection systems. Thank you for the positive feedback!
Prof. Porter Crist –
I’m delighted with the Spray CFD Simulation course using Injection in DPM, ANSYS Fluent Training. I could follow the steps easily, and the spraying effect was nicely visualized. Great job on covering the tracking of water particles!
MR CFD Support –
Thank you for taking the time to share your positive experience with our training course! We’re really glad that you found the material clear and the visualization satisfactory. We take pride in making our simulations easy to follow, and it’s rewarding to know that we were able to assist you in understanding the complex behavior of water particle sprays.
Mrs. Piper Steuber II –
I’m thrilled with the detailed analysis of the water spray simulation. The tracking of each water particle offers valuable insights. Fantastic work!
MR CFD Support –
Thank you so much for the positive feedback! We’re pleased to hear our detailed analysis exceeded your expectations. Stay tuned for more insightful simulations!
Gus Kuhn –
I was really impressed with the visualization of the water particles behavior in the cubic space during the spray DPM simulation. Great job in demonstrating particle dispersion from the inlet and how they interact with the environment!
MR CFD Support –
We truly appreciate your feedback! It’s gratifying to know that the visual representation of the water particle’s motion and their interactions were valuable and insightful for you. Thank you for choosing our CFD training materials. We look forward to serving you with continued quality and informative content.