Radiation Heat Transfer in a Computer Room
$120.00 Student Discount
- The problem numerically simulates the air conditioning of a computer room containing four computers using ANSYS Fluent software.
- We design the 3-D model with the Design Modeler software.
- We mesh the model with ANSYS Meshing software, and the element number equals 809037.
- We use the Surface to Surface (S2S) model to define the Radiation model.
- We use the ideal gas model to consider buoyancy force.
Click on Add To Cart and obtain the Geometry file, Mesh file, and a Comprehensive ANSYS Fluent Training Video.
To Order Your Project or benefit from a CFD consultation, contact our experts via email ([email protected]), online support tab, or WhatsApp at +44 7443 197273.
There are some Free Products to check our service quality.
If you want the training video in another language instead of English, ask it via [email protected] after you buy the product.
Description
Radiation Heat Transfer in a Computer Room CFD Simulation, ANSYS Fluent Training
In this project, the air conditioning of a computer room containing four computers is simulated by ANSYS Fluent software.
The present model consists of a computer room with different heat sources. The present model is designed in three dimensions using Design Modeler software.
Since the geometry is symmetric, only one-quarter of the geometry is modeled. This quadrilateral geometry consists of two sloping glass and steps carrying water flow.
The meshing of the model has been done using ANSYS Meshing software. The element number is 809037.
CFD Methodology
In this project, steady airflow enters the domain from the bottom of the room by several inlets and leaves the domain from several outlets on the ceiling, considering Radiation heat transfer.
This new air conditioning method is commonly used in office environments. This method provides more energy efficiency since the flow naturally goes upwards due to density difference and buoyancy body force.
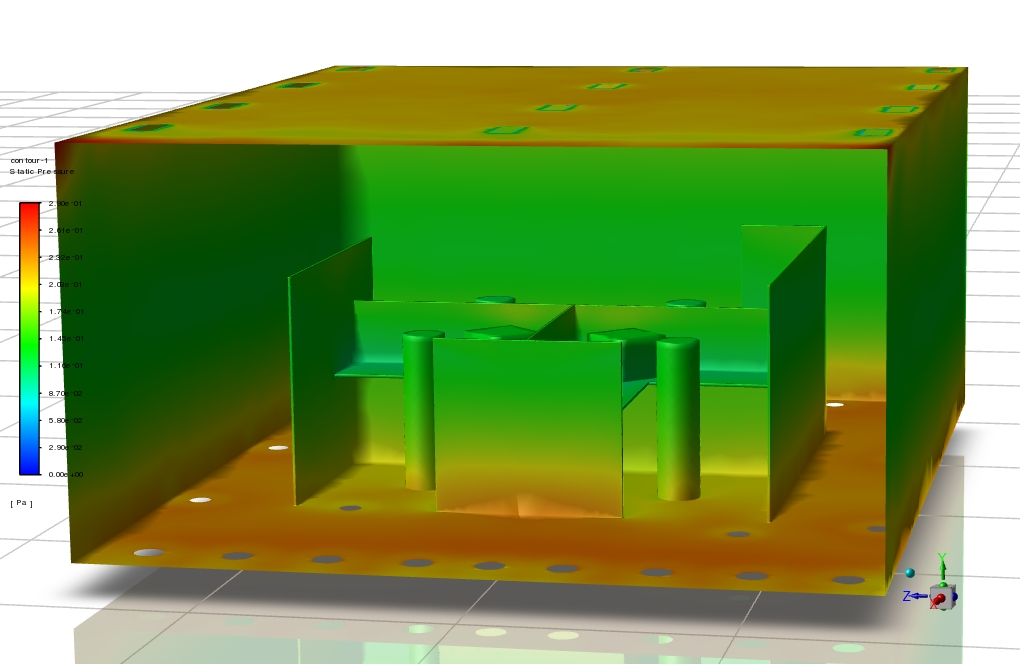
Fresh air enters the computational domain with a velocity of 0.61254m/s and a temperature of 291.8K. One of the room’s four main walls is exposed to a constant heat flux equal to 194 W/m2. The other heat sources include a laptop and a simulator with heat fluxes equal to 153.25 and 90.56W/m2, respectively.
A realizable k-epsilon model is used for solving turbulent fluid equations. The energy equation is enabled to calculate temperature change within the domain, and the ideal gas model is used to account for air density change due to temperature change.
Most importantly, the Surface to Surface (S2S) model is exploited to simulate the radiative heat transfer inside the computational domain.
Radiation Heat Transfer Conclusion
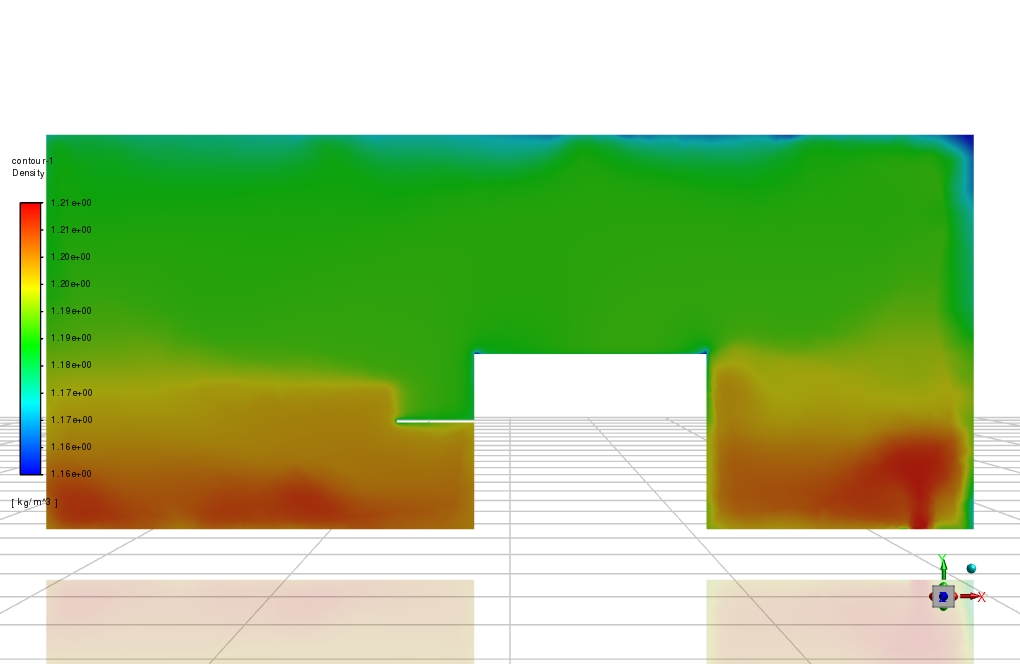
The mixture mass flow rate at the Computer room outlet is 0.568 kg/s. The air density has the minimum value on surfaces that heat flux is applied to due to increased fluid temperature, density decreases, and upward buoyant force affects the fluid volume.
It can be seen that the higher we go along room height, the less air density is observed. High temperatures equal to 327 k are observed on laptop surfaces and hot walls.
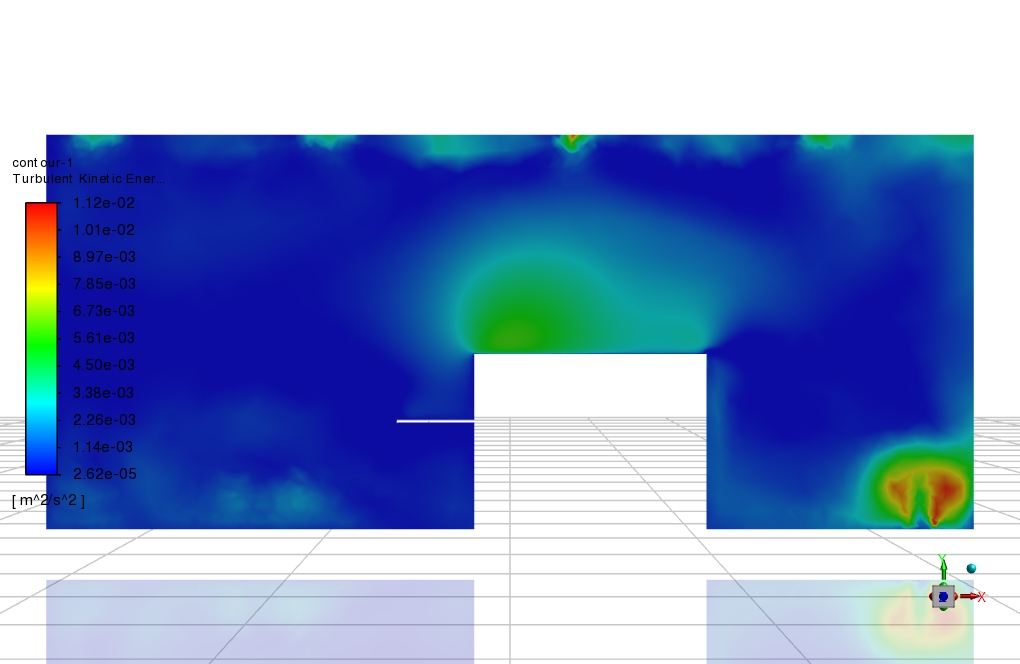
Extreme turbulence can be seen on the hot wall and the top of the simulator’s head. The reason is the consideration of high heat fluxes for laptops, simulators, and hot walls.







Elyse Macejkovic –
Can the simulation model the effect of different ambient conditions?
MR CFD Support –
Absolutely! The ambient temperature and humidity can be adjusted based on your specific conditions. This can affect the heat transfer and air flow in the computer room.
Mr. Brain Harris –
How does the simulation handle the conduction and convection heat transfer?
MR CFD Support –
The simulation solves the energy equation, which includes terms for conduction and convection heat transfer. This ensures a comprehensive model of the heat transfer in the computer room.
Conrad Herzog –
How is the radiation heat transfer modeled in this simulation?
MR CFD Support –
The simulation uses the Discrete Ordinates (DO) model to solve the Radiative Transfer Equation (RTE) and accurately capture the radiation heat transfer in the computer room.
Prof. Alex Hayes Sr. –
I’m thrilled with the detail of simulation! But could you please explain if it’s possible to run this kind of simulation with lower-quality mesh and still get accurate results?
MR CFD Support –
Thank you for your positive feedback! In CFD simulations, mesh quality is critical for accuracy, however, some simulations can be run with a coarser mesh if they have larger tolerances for error. The trade-off with a lower-quality mesh is a potential decrease in result precision, particularly in areas of high gradient like near heat sources. It’s important to perform a mesh sensitivity analysis to understand how mesh quality affects your simulation. Rest assured, if the results’ accuracy is less crucial for certain studies or if computational resources are limited, a coarser mesh could be used with careful considerations.
Roslyn Greenfelder –
The step-by-step guide to simulating radiation heat transfer was incredibly helpful—particularly the use of the S2S model. It gave me a solid understanding of setting up similar scenarios in ANSYS.
MR CFD Support –
Thank you for your thoughtful review! We’re delighted you found the guide helpful and that it could enhance your understanding of radiation heat transfer simulations in ANSYS Fluent. We strive to provide clear and practical instructions in our training materials. If you need any further assistance or advanced guides on CFD simulation, don’t hesitate to reach out!
Ayden Kilback –
This training module opened my eyes to the dynamic world of CFD in practical scenarios. The realizable k-epsilon model effectively illustrated the complexities of turbulent airflow in an office environment. The integration of S2S radiation heat transfer highlighted the intricate balance between different heat sources. Insights gained from observing the changes in air density and temperature distributions were invaluable. Great work on encapsulating such a rich, multifaceted simulation within ANSYS Fluent!
MR CFD Support –
Thank you so much for your kind words! We’re thrilled to hear that our training module on ‘Radiation Heat Transfer in a Computer Room’ proved to be insightful and enriched your understanding of CFD applications. We strive to present comprehensive simulations that resonate with real-world situations. Your understanding of the various elements within the simulation, from buoyancy body force to radiative heat transfer, is exactly what we aim for. It’s great to know it was beneficial for your learning experience!
Mollie Zieme –
I was very impressed with the detailed setup for the computer room’s radiation heat transfer simulation. The integration of multiple heat sources along with airflow and the use of the Surface to Surface model for radiation made it quite comprehensive. How does the density variation due to temperature change affect the overall airflow pattern in this simulation?
MR CFD Support –
In this simulation, the temperature rise causes air density to decrease near the heat sources due to the ideal gas behavior. This reduction in density generates buoyancy forces, which cause the air to rise. As the warmer, less dense air rises, cooler, denser air is drawn in through the inlets at the bottom of the room. This natural convection cycle helps distribute the air within the room, thereby impacting the airflow patterns and contributing to the efficiency of the air conditioning system.
Tyreek Fadel –
I really appreciated how the Radiation Heat Transfer in a Computer Room CFD Simulation material was presented. The step-by-step workflow in ANSYS Fluent was elucidating, from setting up the model, meshing, to solving and analyzing the results. The simulation helped me understand the impact of radiant heat and the airflow patterns in a typical computer room. Stellar job by MR CFD in creating such a comprehensive training module!
MR CFD Support –
Thank you for your kind words! We’re thrilled that our training module on Radiation Heat Transfer in a Computer Room CFD Simulation provided you with a clear understanding and practical insights. It’s wonderful to hear that you found the tutorial helpful and the workflow in ANSYS Fluent easy to follow. We take pride in offering high-quality educational tools to assist our customers in mastering CFD strategies. Your satisfaction fuels our commitment to delivering exceptional learning experiences.
Dejon Mann –
I enjoyed seeing how you simulated the air conditioning in a computer room, taking into account different heat sources. It’s impressive how this method allows for energy efficiency by utilizing natural airflow. I’m curious, did the results help in determining any specific adjustments that could further optimize the cooling system?
MR CFD Support –
Thank you for your positive feedback! Yes, the results did indeed help in identifying areas of improvement. The simulation provided insights into the airflow pattern and temperature distribution, which can be used to adjust the placement of inlets and outlets, as well as the operation of the cooling equipment to further optimize the cooling performance and enhance energy efficiency.
Baby Fadel –
This training package looks really comprehensive. I like how it covers the application of radiation heat transfer principles to an everyday scenario like a computer room. Well, presented!
MR CFD Support –
Thank you for the positive feedback! We’re thrilled that you found our training on radiation heat transfer in a computer room with ANSYS Fluent comprehensive and applicable to real-world scenarios. Your comments are greatly appreciated!
Minerva Kuphal –
The details provided in the training materials for the radiation heat transfer simulation were very insightful and practical, especially understanding how air naturally moves upwards due to density differences in an office environment. Great content for getting a grip on real-world CFD applications!
MR CFD Support –
Thank you! We’re glad you found our training material insightful and practical. Understanding real-world CFD applications is our goal and it’s rewarding to see our content supports this. If you have any further questions or need additional information on our products, feel free to get in touch!
Sheila Becker –
I finally understand why my office AC is more effective! The air conditioning technique in this CFD simulation shows intelligent use of natural air movement and energy efficiency. Really insightful how radiation heat transfer plays a role in creating that comfortable environment around computers. Good job on illustrating those thermal interactions with such precision. It definitely makes the data more relatable and useful.
MR CFD Support –
Thank you for your kind feedback! We strive to provide detailed insights and accurate simulations to help elucidate complex phenomena such as radiation heat transfer. If you have any more questions or require further assistance, feel free to ask.
Casper Mertz –
This learning product really bolstered my understanding of how radiation influences temperature distribution in practical applications like computer room AC systems. The detailed numerical visualization provided by this simulation made complex heat transfer concepts quite tangible and understandable. Great work on the course material and simulation setup!
MR CFD Support –
Thank you for your positive feedback! We’re thrilled to hear that our course material on Radiation Heat Transfer in a Computer Room could clarify complex concepts and offer useful insights into practical heat transfer applications. Your understanding and appreciation motivate us to continue delivering high-quality training programs. If you need further information or assistance, please don’t hesitate to reach out.
Jesse Dickens –
I’m deeply fascinated by the attention to detail in this simulation, particularly the energy-efficient air conditioning concept that uses natural buoyancy forces. It’s a satisfying blend of ingenuity and practicality that addresses real-world efficiency issues.
MR CFD Support –
Thank you for your kind remarks! We work hard to ensure our simulations are as realistic and relevant as possible. It’s gratifying to know when our efforts resonate with our users, and the application of natural phenomena for energy conservation is an area we’re particularly proud of. Thank you for acknowledging our dedication to real-world simulation accuracy.
Julius Boyle –
Absolutely thrilled with the way radiation heat transfer was handled in the simulation of a computer room using ANSYS Fluent. The S2S model’s application to simulate the complexities of radiative heat transfers sounds exceptionally detailed.
MR CFD Support –
Thank you for your kind words! We are glad to hear that you appreciated the complexity and the detail involved in using the S2S model for the radiation heat transfer simulation in a computer room. Our goal is to provide simulations that are as close to real-life scenarios as possible. Your feedback is an encouragement for our team to continue delivering high-quality CFD training using ANSYS Fluent.
Sarai Koelpin –
I’ve followed the guidelines on your simulation of Radiation Heat Transfer in the computer room and got impressive results! The simulation detail is outstanding and seeing the effects of heat fluxes on airflow was educational. Your thorough approach to meshing and the S2S model application for radiative transfer is commendable. Thank you for such a well-structured learning tool.
MR CFD Support –
We sincerely appreciate your positive feedback on our Radiation Heat Transfer in a Computer Room CFD Simulation training product. We are delighted to know that you found the simulation detailed and educational. Our team is dedicated to providing well-structured learning tools for a better understanding of complex phenomena like radiative heat transfer. Thank you for choosing MR CFD Company’s learning products, and we look forward to assisting you in future learning endeavors!
Susan Lehner –
I’m thrilled with the level of detail in the radiation heat transfer simulation you’ve performed for a computer room environment. The approach with the buoyancy effect and the usage of S2S model for radiation showcases a thorough understanding of practical thermodynamics in airflow and temperature management. Additionally, exploiting different heat sources like computers and simulating their impact on air circulation and temperature distribution is very insightful for energy efficiency studies.
MR CFD Support –
Thank you very much for your kind words and recognition of the intricate details involved in our simulation of radiation heat transfer in a computer room. We strive for accuracy and relevance to real-world applications in all our simulations to provide beneficial insights for fields like energy efficiency and thermal management. We are delighted to hear that our approach has met your approval and has been insightful for your understanding.
Dr. Isabell Schoen III –
I am thrilled with the thorough analysis of the Radiation Heat Transfer in the Computer Room using ANSYS Fluent. The attention to detail, such as incorporating different heat sources – the laptop, simulator, and wall, made the simulation real-world applicable. The innovative use of the S2S model to simulate radiative heat transfer provided an in-depth understanding of how the temperature gradients affect air density and flow within the room. I appreciate how the simulation captures the essence of energy-efficient air conditioning methods used in office environments.
MR CFD Support –
We are grateful for your comprehensive review and acknowledgment of the precision in our Radiation Heat Transfer simulation. It’s rewarding to know that the effort put into capturing the intricate details of thermal management in computer rooms is truly valued. Our goal is to provide simulations that not only reflect accurate real-world scenarios but are also beneficial for learning and application in energy efficiency. Your feedback motivates us to uphold these standards. Thank you for choosing our ANSYS Fluent training product!
Landen Nienow –
The simulation touches on S2S radiation modeling; can you clarify how this affects the overall temperature distribution within the room?
MR CFD Support –
In the simulation, the Surface to Surface (S2S) radiation model accounts for the heat exchange between surfaces through thermal radiation. This contributes to the overall temperature distribution by transferring heat from hotter surfaces to cooler ones, affecting both the air temperature and the surface temperatures of the objects within the room. It helps achieve a more accurate prediction of thermal comfort and energy efficiency.
Carrie Torphy –
Wonderful training material! The detailed project covers not only general airflow and cooling concepts but also the interaction of radiation heat transfer within an enclosed space. I have gained a deeper understanding of how different heat sources and cooling strategies can be simulated effectively to mimic real-life conditions. Utilizing one quarter of the geometry for the simulation due to symmetry is a smart way to optimize computational resources. The comprehensive explanation of the set-up, methodologies, and conclusions really solidified my learning experience, especially the simulation of buoyancy effects and how they influence airflow. Well done, MR CFD!
MR CFD Support –
Thank you very much for your kind words! We’re thrilled to hear that our training material on ‘Radiation Heat Transfer in a Computer Room’ was insightful and helped deepen your understanding of the CFD concepts. At MR CFD, we strive to create informative and resource-efficient simulations for an enriching learning experience. It’s great to know that the strategy for handling symmetry and the application of realistic boundary conditions for heat sources were particularly beneficial to you. Your feedback is invaluable, and we look forward to providing more quality educational content!
Adam Waelchi DDS –
I was very impressed with the accuracy of the predicted temperatures and air flow patterns around the various heat sources. It’s fascinating to see how computational fluid dynamics can visually illustrate the hot spots and the efficiency of the air conditioning system in a computationally modeled environment. Great work MR CFD!
MR CFD Support –
Thank you so much for your positive feedback! We’re thrilled to hear that our simulation results provided you with clear insights into the heat transfer and flow dynamics within the computer room scenario. It is our aim to deliver accurate and informative analyses using CFD, and we appreciate you noticing the details and effectiveness. If you have any more questions or need further assistance, feel free to reach out to us!
Lacy Lockman –
I’m impressed by the detailed analysis of how radiation heat transfer was simulated in the computer room, especially how the S2S model was used effectively. Thanks for the clear explanation of the process and outcomes!
MR CFD Support –
Thank you so much for your kind words! We’re thrilled to hear that our product met your expectations and provided a clear understanding of radiation heat transfer in a computer room using the S2S model. Your feedback is greatly appreciated, and it encourages us to continue delivering high-quality CFD simulations and training material. If you have any more questions or need further assistance, please don’t hesitate to ask!
Dr. Marley Funk Sr. –
I am truly impressed with the Radiation Heat Transfer in a Computer Room simulation project. The attention to detail, especially in incorporating various heat sources and using a realizable k-epsilon model, showcases a high level of precision. The use of the S2S model for radiative heat transfer is a sophisticated choice that I’m sure has contributed to the quality of the results. Excellent work on creating an efficient air conditioning simulation!
MR CFD Support –
Thank you for your positive feedback on the Radiation Heat Transfer in a Computer Room simulation. We are delighted to hear that you appreciate the level of detail and precision in our work. The S2S model has indeed been significant in accurately simulating radiative heat transfer within the room. We’re grateful for your recognition of the effort put into orchestrating an energy-efficient air conditioning simulation. Your satisfaction is of utmost importance to us!
Jasper Schuster –
I am truly delighted with the attention to detail in the radiation heat transfer analysis for the computer room CFD simulation tutorial. The integration of S2S radiation model with buoyancy-driven flow wonderfully addresses the complex thermal environment in such spaces.
MR CFD Support –
Thank you for your positive feedback on our Radiation Heat Transfer in a Computer Room CFD Simulation tutorial. We’re thrilled to hear that the detail and integration of the radiation model met your expectations and provided valuable insights.
Dr. Hanna Jacobson –
This training seems comprehensive! The detailed explanation provides clarity on the simulation process and the energy efficiency of the method.
MR CFD Support –
Thank you for your positive feedback! We’re pleased to hear that the detailed explanations in our Radiation Heat Transfer in a Computer Room training were helpful and provided clear insights into the simulation process. Our goal is to deliver comprehensive and understandable CFD training materials. We’re glad you found the information on energy efficiency valuable. If you have any more questions or need further information, feel free to reach out.
Aniya Goodwin –
I am thoroughly impressed with how the Radiation Heat Transfer in a Computer Room simulation was able to model the different heat sources and their effects on airflow and temperature distribution. The inclusion of both convection and radiation heat transfer processes adds to the realism and applicability of the training for real-world scenarios.
MR CFD Support –
Thank you for your positive review of the Radiation Heat Transfer in a Computer Room CFD simulation. We are delighted to hear that you found the training useful and realistic. It is our goal to provide comprehensive learning tools that accurately represent complex processes and can be applied in real-life situations. Your feedback is greatly appreciated, and we look forward to providing more quality training products.
Willy Fisher –
I wasn’t clear on this from the overview—how exactly did the S2S radiation model influence the airflow patterns in your simulation?
MR CFD Support –
The Surface to Surface (S2S) radiation model accounted for the transfer of thermal radiation between surfaces within the computer room. Since thermal radiation can affect the temperature distribution on solid surfaces—warmer surfaces can heat the adjacent air—it influences the natural convection currents within the room. Radiative heat transfer might increase the temperature of the air in contact with heated surfaces more significantly than the other regions, reinforcing the buoyancy effects and altering the overall airflow patterns. Thus, the vertical temperature gradient and the resulting flow of air upwards are more pronounced.