Solar Radiation Effect on a Gasoline Tank Simulation

Solar Radiation Effect on a Gasoline Tank CFD Simulation, ANSYS Fluent Training

This simulation is about the solar radiation effect on a gasoline tank via ANSYS Fluent software. We perform this CFD project and investigate it by CFD analysis.

The present problem investigates the effect of solar radiation and a coating layer on a gasoline fuel tank. In this model, a fuel tank inside a computational zone contains airflow. The airflow with a velocity of 10 m/s and a temperature of 318.15 K enters the computational zone and collides with the tank.

In this project, the effect of radiation on the model is considered. The characteristics of solar radiation on surfaces and objects include longitude of 36.2605 degrees, latitude of 59.6168 degrees, and a time zone equivalent to 4.5.

The radiation time in the date and time section is defined as 13:08 on the 17th day of the 8th. This simulation has been done in two geometrically different modes. In the first case, no cover layer is provided for the gasoline tank; in the second case, a 0.003 m cover layer is used for the tank’s perimeter.

The geometry of the present model is drawn by Design Modeler software. The present model consists of a cylindrical tank for the storage of gasoline. The model is then meshed by ANSYS Meshing software. The model mesh is unstructured, and 1084362 cells have been created.

Solar Radiation Method

Since the problem’s purpose is to investigate the effect of solar radiation on the tank, the Radiation model has been used. The radiation model is P1 type, and solar ray tracing mode has also been activated.

Model P1 is used for cases where directional independence is integrated into the radiation heat transfer equations, resulting in a scattering or emission equation for random radiation.

Its advantages are that the radiation heat transfer equation is easily solved even with low CPUs, includes the effects of light scattering, such as the effects of particles or droplets of water or soot, and works well in cases with high thicknesses.

The solar load model is also used to activate the thermal load of solar energy.

Solar Radiation Conclusion

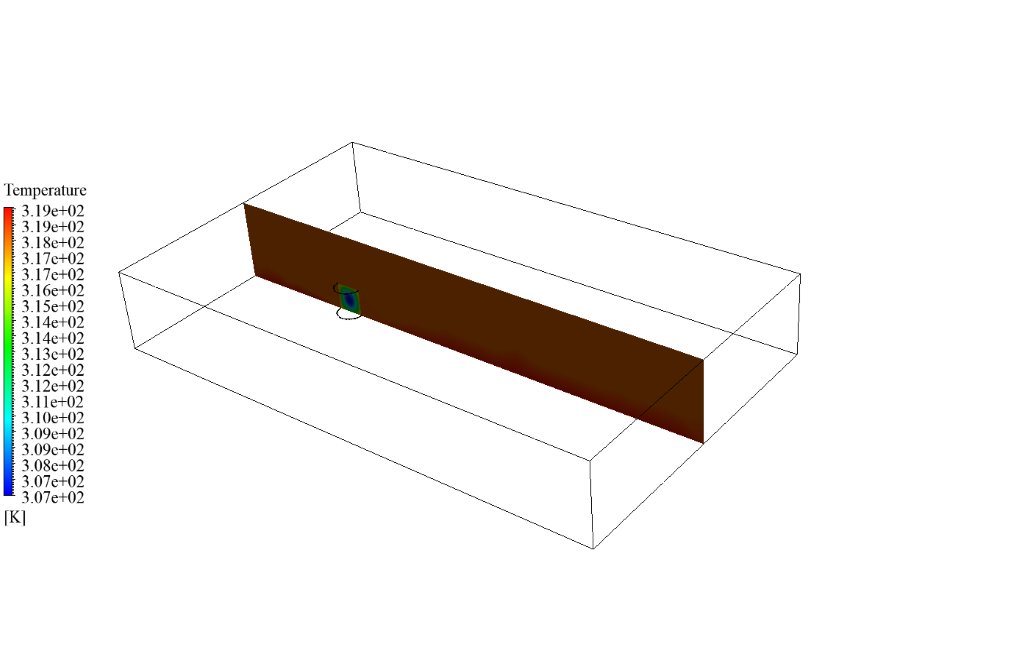
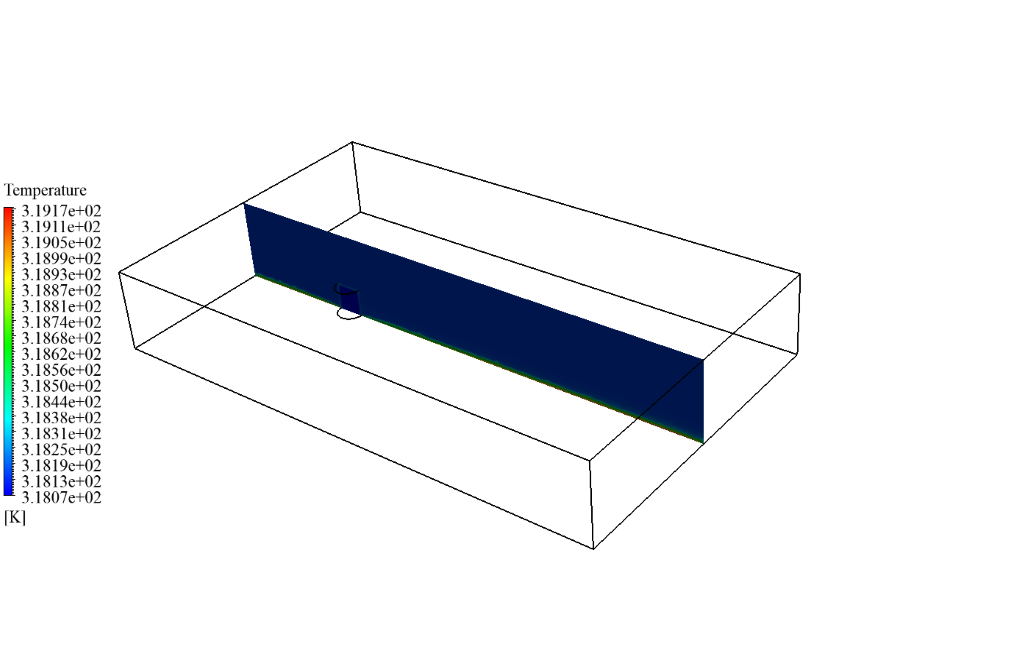
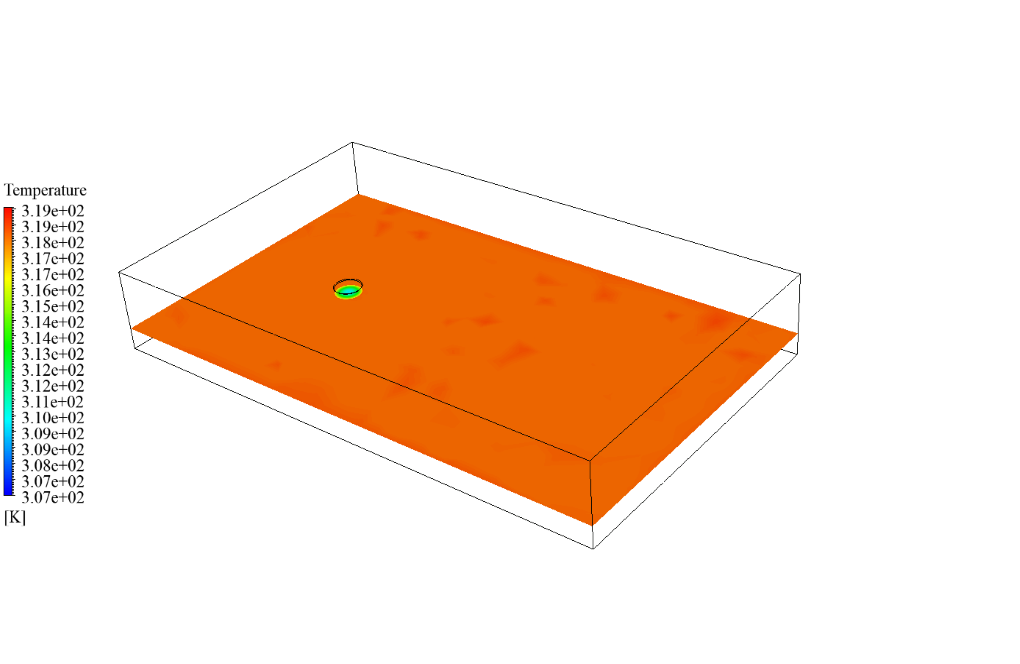
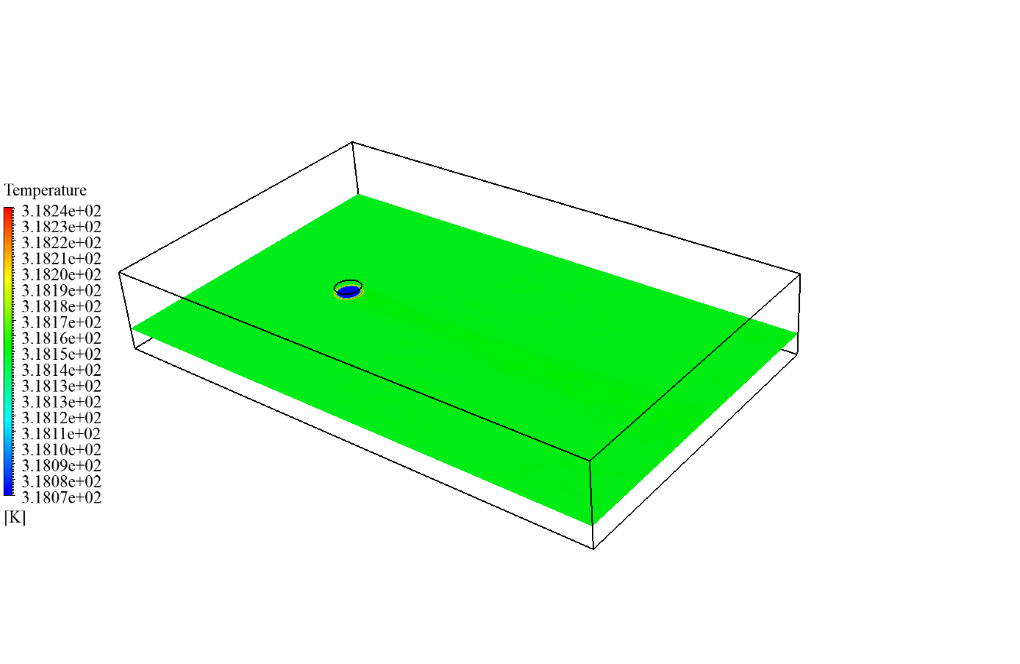
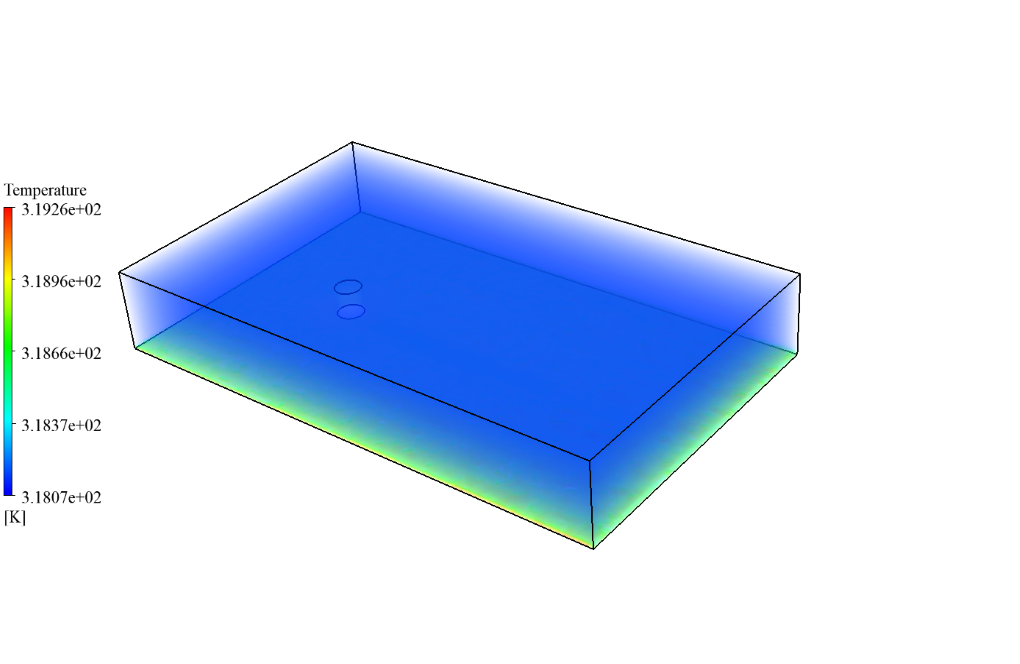
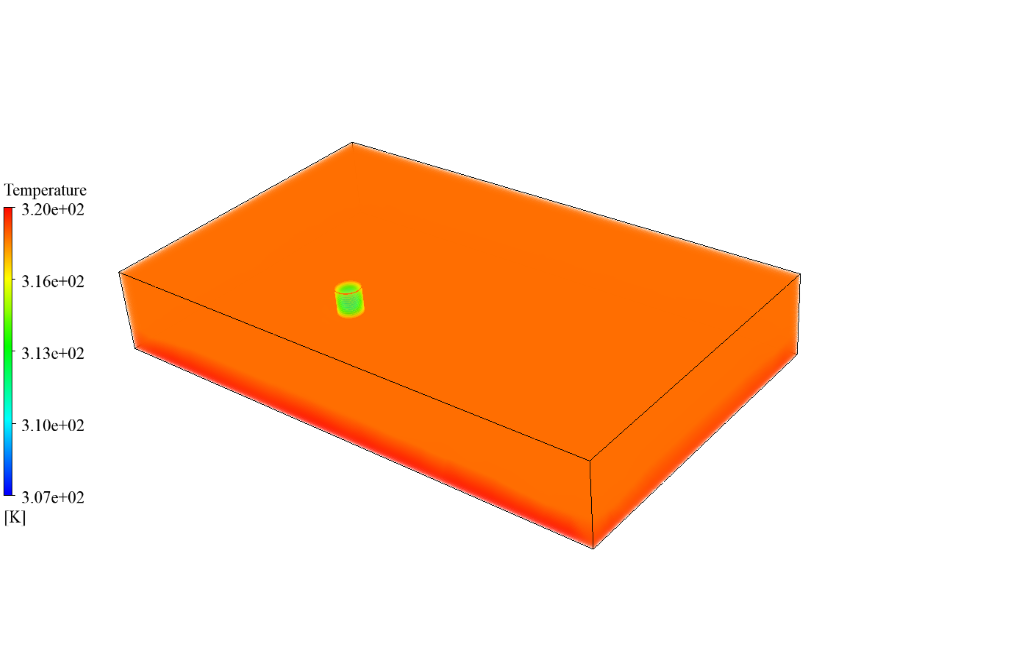
After simulation, we obtain 2D and 3D temperature contours in both cases, including a tank with and without a coating layer. We obtain these contours at the last second of the simulation process. As the contours show, the temperature changes differ in the two cases.

When we don’t use a coating layer, the temperature inside the gasoline tank also rises due to solar ray tracing and radiation heat transfer. However, if we use a coating layer, this layer acts as a barrier against radiation and causes the temperature of the gasoline inside the tank to remain cold.